 Toán 12 Cùng khám phá | Giải toán lớp 12 Cùng khám phá
Toán 12 Cùng khám phá | Giải toán lớp 12 Cùng khám phá
 Bài 2. Các phép toán vecto trong không gian - Toán 12 C..
Bài 2. Các phép toán vecto trong không gian - Toán 12 C..
Giải bài tập 2.3 trang 64 SGK Toán 12 tập 1 - Cùng khám phá
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Chứng minh rằng: \(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD} \)
Đề bài
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Chứng minh rằng:
\(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD} \)
Phương pháp giải - Xem chi tiết
Sử dụng tính chất của hình bình hành và phép biến đổi vectơ.
Lời giải chi tiết
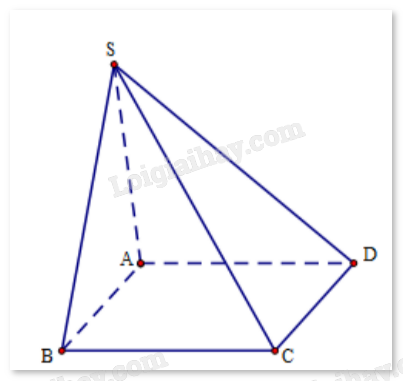
Ta có thể viết:
\(\overrightarrow {SA} + \overrightarrow {SC} = (\overrightarrow {SB} + \overrightarrow {BA} ) + (\overrightarrow {SD} + \overrightarrow {DC} )\)
Thay \(\overrightarrow {BA} = - \overrightarrow {AB} \) và \(\overrightarrow {DC} = - \overrightarrow {CD} \) vào biểu thức trên, ta được:
\(\overrightarrow {SA} + \overrightarrow {SC} = (\overrightarrow {SB} - \overrightarrow {AB} ) + (\overrightarrow {SD} - \overrightarrow {CD} )\)
Sử dụng tính chất của hình bình hành:
\(\overrightarrow {AB} = \overrightarrow {DC} \quad {\rm{và}}\quad \overrightarrow {AD} = \overrightarrow {BC} \)
Nên ta có:
\(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} - \overrightarrow {AB} + \overrightarrow {SD} + \overrightarrow {DC} = \overrightarrow {SB} + \overrightarrow {SD} \)
Vậy đẳng thức \(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD} \) đã được chứng minh.
- Giải bài tập 2.4 trang 64 SGK Toán 12 tập 1 - Cùng khám phá
- Giải bài tập 2.5 trang 65 SGK Toán 12 tập 1 - Cùng khám phá
- Giải bài tập 2.6 trang 65 SGK Toán 12 tập 1 - Cùng khám phá
- Giải bài tập 2.7 trang 65 SGK Toán 12 tập 1 - Cùng khám phá
- Giải bài tập 2.8 trang 65 SGK Toán 12 tập 1 - Cùng khám phá
>> Xem thêm
Các bài khác cùng chuyên mục
- Giải bài tập 6.20 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.19 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.18 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.17 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.16 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.20 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.19 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.18 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.17 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.16 trang 107 SGK Toán 12 tập 2 - Cùng khám phá












Danh sách bình luận