Giải bài 9 trang 12 sách bài tập toán 12 - Cánh diều

• Giải bài 8 trang 11 sách bài tập toán 12 - Cánh diều

  Cho hàm số (y = fleft( x right)) có đạo hàm trên (mathbb{R}) và bảng xét dấu của đạo hàm như sau: Số điểm cực trị của hàm số đã cho là: A. 0. B. 1. C. 2. D. 3.

• Giải bài 10 trang 12 sách bài tập toán 12 - Cánh diều

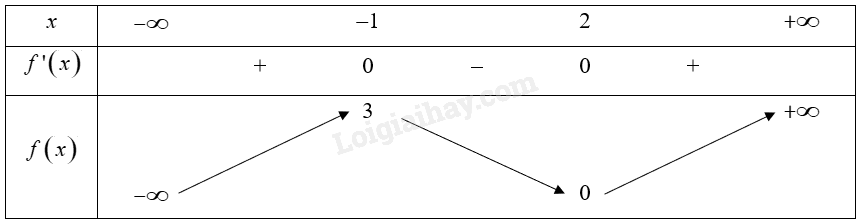
  Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau: Mệnh đề nào dưới đây đúng? A. Hàm số đạt cực tiểu tại \(x = - 5\). B. Hàm số có giá trị cực đại bằng 0. C. Hàm số đạt cực tiểu tại \(x = 2\). D. Hàm số đạt cực đại tại \(x = 4\).

• Giải bài 11 trang 12 sách bài tập toán 12 - Cánh diều

  Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = {x^2}{\left( {{x^2} - 1} \right)^2}\left( {x - 2} \right),\forall x \in \mathbb{R}\). Số điểm cực trị của hàm số đã cho là: A. 1. B. 2. C. 3. D. 4.

• Giải bài 12 trang 12 sách bài tập toán 12 - Cánh diều

  Cho hàm số \(y = 2{x^3} + 3x + 2\). Kết luận nào sau đây là đúng? A. Hàm số có 3 cực trị. B. Hàm số có 2 cực trị. C. Hàm số có 1 cực trị. D. Hàm số không có cực trị.

• Giải bài 13 trang 12 sách bài tập toán 12 - Cánh diều

  Hàm số \(y = {x^3} - 3{x^2} - 9x - 3\) đạt cực tiểu tại điểm: A. ‒1. B. 3. C. 2. D. ‒30.

• Giải bài 14 trang 12 sách bài tập toán 12 - Cánh diều

  Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như Hình 5. Số điểm cực trị của hàm số đã cho là: A. 2. B. 4. C. 1. D. 3.

• Giải bài 15 trang 13 sách bài tập toán 12 - Cánh diều

  Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như Hình 6. Giá trị cực tiểu của hàm số đã cho là: A. 2. B. 1. C. ‒1. D. 0.

• Giải bài 16 trang 13 sách bài tập toán 12 - Cánh diều

  Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và đồ thị hàm số \(y = f'\left( x \right)\) như Hình 7. Số điểm cực trị của hàm số \(y = f\left( x \right)\) là: A. 4. B. 3. C. 2. D. 1.

• Giải bài 17 trang 13 sách bài tập toán 12 - Cánh diều

  Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S). Cho hàm số (y = {x^3} - 3{rm{x}} + 2). a) (y' = 3{{rm{x}}^2} - 3). b) (y' = 0) khi (x = - 1,x = 1). c) (y' > 0) khi (x in left( { - 1;1} right)) và (y' < 0) khi (x in left( { - infty ; - 1} right) cup left( {1; + infty } right)). d) Giá trị cực đại của hàm số là ${{f}_{CĐ}}=0$.

• Giải bài 18 trang 13 sách bài tập toán 12 - Cánh diều

  Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S). Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và đồ thị hàm số \(y = f'\left( x \right)\) như Hình 8. a) \(f'\left( x \right) = 0\) khi \(x = 0,x = 1,x = 3\). b) Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( { - \infty ;0} \right)\). c) \(f'\left( x \right) > 0\) khi \(x \in \left( {0;3} \right)\). d) Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( {0;3} \right)\).

• Giải bài 19 trang 14 sách bài tập toán 12 - Cánh diều

  Tìm các khoảng đơn điệu của mỗi hàm số sau: a) \(y = - \frac{1}{3}{x^3} + {x^2} + 3{\rm{x}} - 1\); b) \(y = {x^3} - 3{x^2} + 3{\rm{x}} - 1\); c) \(y = {x^4} + {x^2} - 2\); d) \(y = - {x^4} + 2{{\rm{x}}^2} - 1\); e) \(y = \frac{{2{\rm{x}} - 3}}{{{\rm{x}} - 4}}\); g) \(y = \frac{{{x^2} + x + 2}}{{x + 2}}\).

• Giải bài 20 trang 14 sách bài tập toán 12 - Cánh diều

  Tìm điểm cực trị của mỗi hàm số sau: a) \(y = {x^3} - 12{\rm{x}} + 8\); b) \(y = 2{{\rm{x}}^4} - 4{{\rm{x}}^2} - 1\); c) \(y = \frac{{{x^2} - 2{\rm{x}} - 2}}{{x + 1}}\); d) \(y = - x + 1 - \frac{9}{{x - 2}}\)

• Giải bài 21 trang 14 sách bài tập toán 12 - Cánh diều

  Dùng đạo hàm của hàm số, hãy giải thích: a) Hàm số \(y = {a^x}\) đồng biến trên \(\mathbb{R}\) khi \(a > 1\), nghịch biến trên \(\mathbb{R}\) khi \(0 < a < 1\). b) Hàm số \(y = {\log _a}x\) đồng biến trên khoảng \(\left( {0; + \infty } \right)\) khi \(a > 1\), nghịch biến trên khoảng \(\left( {0; + \infty } \right)\) khi \(0 < a < 1\).

• Giải bài 22 trang 14 sách bài tập toán 12 - Cánh diều

  Chứng minh rằng: a) Hàm số \(y = \sqrt {{x^2} - 4} \) nghịch biến trên khoảng \(\left( { - \infty ; - 2} \right)\) và đồng biến trên khoảng \(\left( {2; + \infty } \right)\). b) Hàm số \(y = \ln \left( {{x^2} + 1} \right)\) nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\) và đồng biến trên khoảng \(\left( {0; + \infty } \right)\). c) Hàm số \(y = {2^{ - {x^2} + 2x}}\) đồng biến trên khoảng \(\left( { - \infty ;1} \right)\) và nghịch biến trên khoảng \(\left( {1; + \infty } \right)\).

• Giải bài 23 trang 14 sách bài tập toán 12 - Cánh diều

  Tìm điểm cực trị của mỗi hàm số sau: a) (y = x.{e^x}); b) (y = {left( {x + 1} right)^2}.{e^{ - x}}); c) (y = {x^2}.ln {rm{x}}); d) (y = frac{x}{{ln {rm{x}}}}).

• Giải bài 24 trang 14 sách bài tập toán 12 - Cánh diều

  Trong một thí nghiệm y học, người ta cấy 1 000 con vi khuẩn vào môi trường dinh dưỡng. Bằng thực nghiệm, người ta xác định được số lượng vi khuẩn thay đổi theo thời gian bởi công thức: \(N\left( t \right) = 1000 + \frac{{100t}}{{100 + {t^2}}}\) trong đó \(t\) là thời gian tính bằng giây \(\left( {t \ge 0} \right)\) (Nguồn: R. Larson and B. Edwards, Calculus 10e, Cengage 2014). Trong khoảng thời gian nào từ lúc nuôi cấy, số lượng vi khuẩn sẽ tăng lên?

• Giải bài 25 trang 15 sách bài tập toán 12 - Cánh diều

  Trong 5 giây đầu tiên, một chất điểm chuyển động theo phương trình \(s\left( t \right) = {t^3} - 6{t^2} + 14t + 1\) trong đó \(t\) tính bằng giây và \(s\) tính bằng mét. Trong khoảng thời gian nào của 5 giây đầu tiên thì vận tốc tức thời của chất điểm tăng lên?

• Giải bài 7 trang 11 sách bài tập toán 12 - Cánh diều

  Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như Hình 4. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

• Giải bài 6 trang 11 sách bài tập toán 12 - Cánh diều

  Trong các hàm số sau, hàm số đồng biến trên \(\mathbb{R}\) là:

• Giải bài 5 trang 11 sách bài tập toán 12 - Cánh diều

  Cho hàm số (y = frac{x}{{x - 1}}). Mệnh đề nào dưới đây là đúng?

• Giải bài 4 trang 11 sách bài tập toán 12 - Cánh diều

  Cho hàm số \(y = - {x^3} + 3{x^2} - 4\). Mệnh đề nào dưới đây là đúng?

• Giải bài 3 trang 10 sách bài tập toán 12 - Cánh diều

  Cho hàm số (y = fleft( x right)) có đạo hàm (f'left( x right) = - xleft( {2x - 5} right),forall x in mathbb{R}). Khẳng định nào dưới đây đúng?

• Giải bài 2 trang 10 sách bài tập toán 12 - Cánh diều

  Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:

• Giải bài 1 trang 10 sách bài tập toán 12 - Cánh diều

  Cho hàm số (y = fleft( x right)) có bảng xét dấu của đạo hàm (f'left( x right)) như sau

>> Xem thêm