Giải bài 16 trang 13 sách bài tập toán 12 - Cánh diều
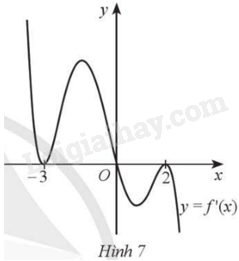
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và đồ thị hàm số \(y = f'\left( x \right)\) như Hình 7. Số điểm cực trị của hàm số \(y = f\left( x \right)\) là: A. 4. B. 3. C. 2. D. 1.
Đề bài
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và đồ thị hàm số \(y = f'\left( x \right)\) như Hình 7. Số điểm cực trị của hàm số \(y = f\left( x \right)\) là:
A. 4.
B. 3.
C. 2.
D. 1.
Phương pháp giải - Xem chi tiết
Dựa vào đồ thị hàm số \(y = f'\left( x \right)\), lập bảng xét dấu đạo hàm của hàm số \(y = f\left( x \right)\), từ đó xác định số điểm cực trị của hàm số \(y = f\left( x \right)\).
Lời giải chi tiết
Do hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) nên hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\).
Căn cứ vào đồ thị hàm số \(y = f'\left( x \right)\), ta có:
\(f'\left( x \right) = 0\) khi \(x = - 3,x = 0,x = 2\). Dựa vào vị trí của đồ thị hàm số \(y = f'\left( x \right)\) so với trục hoành, ta có bảng xét dấu \(f'\left( x \right)\) như sau:

Hàm số đạt cực đại tại \(x = 0\). Vậy hàm số có 1 cực trị.
Chọn D.













Danh sách bình luận