Giải bài 7.5 trang 26 sách bài tập toán 11 - Kết nối tri thức với cuộc sống

Một chiếc thang có dạng hình thang cân cao (6{rm{;m}}), hai chân thang cách nhau (80{rm{;cm}})

Đề bài

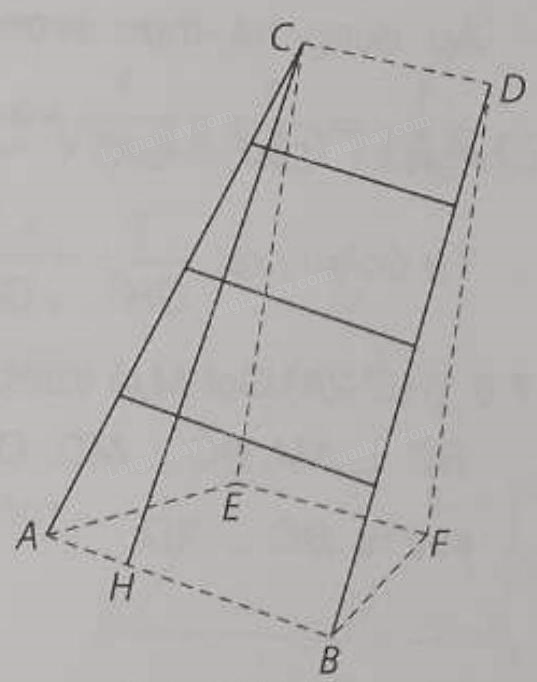
Một chiếc thang có dạng hình thang cân cao \(6{\rm{\;m}}\), hai chân thang cách nhau \(80{\rm{\;cm}}\), hai ngọn thang cách nhau \(60{\rm{\;cm}}\).Thang được dựa vào bờ tường như hình bên. Tính góc tạo giữa đường thẳng chân tường và cạnh cột thang (tính gần đúng theo đơn vị độ, làm tròn kết quả đến chữ số thập phân thứ hai).

Phương pháp giải - Xem chi tiết

Gọi \(A,B\) là hai điểm tại hai vị tri chân thang và \(C,D\) là hai điểm tại hai vị trí ngọn thang, \(EF\) là đường chân tường.

Ta có \(EF//AB\) nên \(\left( {EF,AC} \right) = \left( {AB,AC} \right) = \widehat {BAC}\).

Kẻ \(CH\) vuông góc với \(AB\) tại \(H\), tính \(AH = \frac{{AB - CD}}{2}\).

Tam giác \(ACH\) vuông tại \(H\) nên \({\rm{cos}}\widehat {CAH}\), suy ra \(\widehat {CAH}\)

Lời giải chi tiết

Gọi \(A,B\) là hai điểm tại hai vị tri chân thang và \(C,D\) là hai điểm tại hai vị trí ngọn thang, \(EF\) là đường chân tường. Ta có \(EF//AB\) nên \(\left( {EF,AC} \right) = \left( {AB,AC} \right) = \widehat {BAC}\).

Kẻ \(CH\) vuông góc với \(AB\) tại \(H\), khi đó \(AH = \frac{{AB - CD}}{2} = 10\left( {{\rm{\;cm}}} \right) = 0,1\left( {{\rm{\;m}}} \right)\).

Tam giác \(ACH\) vuông tại \(H\) nên \({\rm{cos}}\widehat {CAH} = \frac{{AH}}{{AC}} = \frac{{0,1}}{6} = \frac{1}{{60}}\), suy ra \(\widehat {CAH} \approx 89,{05^ \circ }\).