-
SBT TOÁN TẬP 1 - CÁNH DIỀU
-
SBT TOÁN TẬP 2 - CÁNH DIỀU
SBT Toán 11 - giải SBT Toán 11 - Cánh diều
Bài 6. Phép chiếu song song. Hình biểu diễn của một hìn..
Giải bài 49 trang 117 sách bài tập toán 11 - Cánh diều
Hình biểu diễn của hai đường thẳng chéo nhau có thể là hai đường thẳng song song được không? Vì sao?
Đã có lời giải SGK Toán lớp 12 - Cánh diều (mới)
Đầy đủ - Chi tiết - Chính xác
Đề bài
Hình biểu diễn của hai đường thẳng chéo nhau có thể là hai đường thẳng song song được không? Vì sao?
Phương pháp giải - Xem chi tiết
Giả sử hai đường thẳng \(a\) và \(b\) chéo nhau và hình chiếu song song của \(a\), \(b\) theo phương chiếu là đường thẳng bất kỳ \(l\) lần lượt là \(a'\), \(b'\) trên cùng một mặt phẳng. Ta cần xác định xem \(a'\) và \(b'\) có song song với nhau không.
Lời giải chi tiết
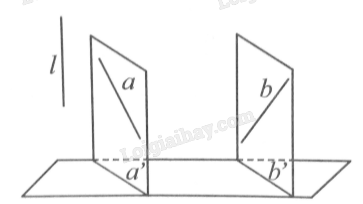
Giả sử hai đường thẳng \(a\) và \(b\) chéo nhau và hình chiếu song song của \(a\), \(b\) theo phương chiếu là đường thẳng bất kỳ \(l\) lần lượt là \(a'\), \(b'\) trên cùng một mặt phẳng. Ta nhận thấy rằng nếu mặt phẳng chứa hai đường thẳng \(a\) và \(a'\) (kí hiệu là \(\left( {a,a'} \right)\)) song song với mặt phẳng \(\left( {b,b'} \right)\) thì do \(a'\) và \(b'\) cùng nằm trên mặt phẳng chiếu, nên chúng song song với nhau.
Như vậy, hình biểu diễn của hai đường thẳng chéo nhau có thể là hai đường thẳng song song
Bình luận
Chia sẻ
Luyện Bài Tập Trắc nghiệm Toán 11 - Cánh diều - Xem ngay
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
