SBT Toán 7 - giải SBT Toán 7 - Cánh diều Bài tập cuối chương 4 - Cánh diều

Giải Bài 43 trang 116 sách bài tập toán 7 tập 1 - Cánh diều


Cho Hình 53 có OC và DE cùng vuông góc với OD,

Đề bài

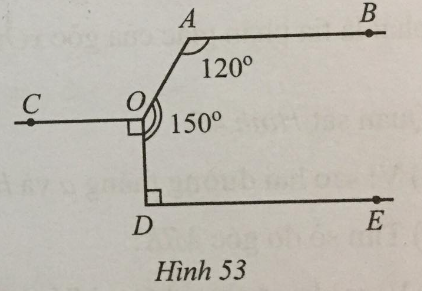
Cho Hình 53 có OC và DE cùng vuông góc với OD, \(\widehat {BAO} = 120^\circ ,{\rm{ }}\widehat {AOD} = 150^\circ \).

Chứng tỏ rằng AB // OC // DE.

 

Phương pháp giải - Xem chi tiết

Muốn chứng tỏ rằng AB // OC // DE ta chứng minh chúng cùng vuông góc với một đường thẳng hoặc chúng có các cặp góc bằng nhau và ở một trong các vị trí: so le trong, so le ngoài, đồng vị.

Lời giải chi tiết

Ta có: OC và DE cùng vuông góc với OD nên OC // DE.

Ta có: \(\widehat {COA} = 360^\circ  - \widehat {COD} - \widehat {DOA} = 360^\circ  - 90^\circ  - 150^\circ  = 120^\circ \).

Suy ra: \(\widehat {COA} = \widehat {OAB} = 120^\circ \) mà hai góc này ở vị trí so le trong nên OC // AB.

Vậy AB // OC // DE.


Bình chọn:
4 trên 9 phiếu

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 7 - Cánh diều - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store