Giải bài 40 trang 75 sách bài tập toán 8 – Cánh diều

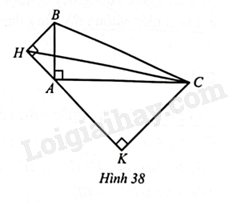
Hình 38 cho tam giác \(ABC\) vuông ở \(A\), \(AB = 5\)cm, \(AC = 12\)cm. Tam giác \(HAB\) vuông cân tại \(H\), tam giác \(KAC\) vuông cân tại \(K\).

Đề bài

Hình 38 cho tam giác \(ABC\) vuông ở \(A\), \(AB = 5\)cm, \(AC = 12\)cm. Tam giác \(HAB\) vuông cân tại \(H\), tam giác \(KAC\) vuông cân tại \(K\). Các cặp tam giác sau có đồng dạng với nhau không? Vì sao?

a) Tam giác \(HAB\) và tam giác \(KAC\).

b) Tam giác \(HKC\) và tam giác \(BAC\).

Phương pháp giải - Xem chi tiết

Áp dụng trường hợp đồng dạng thứ hai của tam giác vào tam giác vuông:

Nếu hai cạnh góc vuông của tam giác vuông này tỉ lệ với hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.

Lời giải chi tiết

a) Tam giác \(HAB\) vuông cân tại \(H\) và \(AB = 5\)cm nên \(HA = HB = \frac{5}{{\sqrt 2 }}\)cm.

Tam giác \(KAC\) vuông cân tại \(K\) và \(AC = 12\)cm nên \(KA = KC = \frac{{12}}{{\sqrt 2 }}\) cm.

Do \(\widehat {AHB} = \widehat {AKC}\) và \(\frac{{HA}}{{KA}} = \frac{{HB}}{{KC}} = \frac{5}{{12}}\) nên \(\Delta HAB\backsim \Delta KAC\).

b) Tam giác \(HKC\) vuông tại \(K\) và có hai cạnh góc vuông là \(HK = \frac{{17}}{{\sqrt 2 }}\)cm, \(KC = \frac{{12}}{{\sqrt 2 }}\)cm.

Tam giác \(BAC\) vuông tại \(A\) và có hai cạnh góc vuông là \(AB = 5\)cm, \(AC = 12\)cm. Từ đó, dễ thấy tam giác \(HKC\) không đồng dạng với tam giác \(BAC\).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 41 trang 75 sách bài tập toán 8 – Cánh diều
Hình thang \(ABCD\) ở Hình 39 có \(AB//CD,AB < CD,\widehat {ABD} = 90^\circ \). Hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(G\).
Giải bài 42 trang 76 sách bài tập toán 8 – Cánh diều
Cho tam giác \(ABC\) vuông ở \(A\) có \(AB = 3AC\) và điểm \(D\) thuộc cạnh \(AB\) sao cho \(AD = 2DB\). Chứng minh: \(\widehat {ADC} + \widehat {ABC} = 45^\circ \).
Giải bài 43 trang 76 sách bài tập toán 8 – Cánh diều
Cho tam giác \(ABC\) có \(AB = 2\)cm, \(AC = 3\)cm, \(BC = 4\)cm. Chứng minh: \(\widehat {BAC} = \widehat {ABC} + 2\widehat {BCA}\).
Giải bài 39 trang 75 sách bài tập toán 8 – Cánh diều
Trong Hình 37, cho (O) là giao điểm hai đường chéo (AC) và (BD) của tứ giác (ABCD). Kẻ một đường thẳng tùy ý đi qua (O) và cắt cạnh (AB) tại (M,CD) tại (N).
Giải bài 38 trang 75 sách bài tập toán 8 – Cánh diều
Cho tam giác \(ABC\) có \(AB = 12\)cm, \(AC = 18\)cm, \(BC = 27\)cm. Điểm \(D\) thuộc cạnh \(BC\) sao cho \(CD = 12\)cm. Tính độ dài \(AD\).
Giải bài 37 trang 75 sách bài tập toán 8 – Cánh diều
Quan sát Hình 36 và chỉ ra một cặp tam giác đồng dạng: