Giải bài 26 trang 104 sách bài tập toán 11 - Cánh diều

Cho hình chóp \(S.ABCD\) có đáy\(ABCD\) là hình bình hành.

Đề bài

Cho hình chóp \(S.ABCD\) có đáy\(ABCD\) là hình bình hành. Gọi \(M\) là điểm chuyển động trên cạnh \(SC\) (\(M\) khác \(C\)), \(\left( P \right)\) là mặt phẳng chứa đường thẳng \(AM\) và song song với \(BD\). Chứng minh rằng mặt phẳng \(\left( P \right)\) luôn đi qua một đường thẳng cố định khi \(M\) chuyển động trên cạnh \(SC\).

Phương pháp giải - Xem chi tiết

Sử dụng định lí sau: “Cho đường thẳng \(a\) song song với mặt phẳng \(\left( P \right)\). Mặt phẳng \(\left( Q \right)\) chứa \(a\) và cắt \(\left( P \right)\) theo giao tuyến \(b\) thì \(a\parallel b\).”

Trên mặt phẳng \(\left( {ABCD} \right)\), vẽ đường thẳng \(d\) đi qua \(A\) và song song với \(BD\). Chứng minh rằng \(d \subset \left( P \right)\).

Lời giải chi tiết

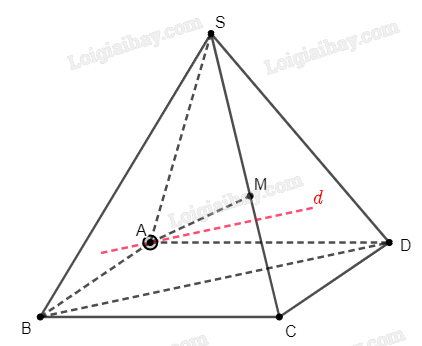
Trên mặt phẳng \(\left( {ABCD} \right)\), vẽ đường thẳng \(d\) đi qua \(A\) và song song với \(BD\).

Xét mặt phẳng \(\left( P \right)\) và \(\left( {ABCD} \right)\), ta có \(A \in AM \subset \left( P \right)\) và \(A \in \left( {ABCD} \right)\) nên giao tuyến của \(\left( P \right)\) và \(\left( {ABCD} \right)\) là đường thẳng đi qua \(A\).

Mặt khác, ta có \(BD\parallel \left( P \right)\), \(BD \subset \left( {ABCD} \right)\) nên giao tuyến của \(\left( P \right)\) và \(\left( {ABCD} \right)\) là một đường thẳng song song với \(BD\).

Do đường thẳng \(d\) đi qua \(A\) và song song với \(BD\) nên \(d\) chính là giao tuyến của \(\left( P \right)\) và \(\left( {ABCD} \right)\).

Vì hình bình hành \(ABCD\) cố định, nên đường thẳng \(d\) cố định.

Vậy mặt phẳng \(\left( P \right)\) luôn đi qua đường thẳng \(d\) cố định.

Bài toán được chứng minh.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 27 trang 105 sách bài tập toán 11 - Cánh diều
Trong các không gian hẹp, người ta thường thiết kế tủ đựng quần áo có cánh cửa trượt
Giải bài 25 trang 104 sách bài tập toán 11 - Cánh diều
Cho hình chóp (S.ABCD) có đáy(ABCD) là hình bình hành.
Giải bài 24 trang 104 sách bài tập toán 11 - Cánh diều
Cho hình chóp \(S.ABCD\) có đáy\(ABCD\) là hình bình hành. Gọi \(M\), \(N\) lần lượt là trung điểm của \(CD\), \(SB\).
Giải bài 23 trang 104 sách bài tập toán 11 - Cánh diều
Cho tứ diện\(ABCD\). Gọi \(M\), \(N\), \(P\), \(Q\) lần lượt là trung điểm của \(AB\), \(AD\), \(BC\), \(CD\).
Giải bài 22 trang 104 sách bài tập toán 11 - Cánh diều
Cho tứ diện \(ABCD\). Gọi \(G\) là trọng tâm của tam giác \(ACD\), điểm \(M\) nằm trên cạnh \(AB\) sao cho \(AM = 2MB\).
Giải bài 21 trang 104 sách bài tập toán 11 - Cánh diều
Cho hai đường thẳng \(a\) và \(b\) chéo nhau. Có bao nhiêu mặt phẳng chứa \(a\) và song song với \(b\)?
Giải bài 20 trang 104 sách bài tập toán 11 - Cánh diều
Cho đường thẳng \(a\) song song với mặt phẳng \(\left( P \right)\). Khẳng định nào sau đây là SAI?
Giải bài 19 trang 104 sách bài tập toán 11 - Cánh diều
Cho đường thẳng \(a\) song song với mặt phẳng \(\left( P \right)\).