-
Toán 8 tập 1 - Cánh diều
-
Toán 8 tập 2 - Cánh diều
-
Chương 6 Một số yếu tố thống kê và xác suất
- Bài 1. Thu thập và phân loại dữ liệu
- Bài 2. Mô tả và biểu diễn dữ liệu trên các bảng, biểu đồ
- Bài 3. Phân tích và xử lí dữ liệu thu được ở dạng bảng, biểu đồ
- Bài 4. Xác suất của biến cố ngẫu nhiên trong một số trò chơi đơn giản
- Bài 5. Xác suất thực nghiệm của một biến cố trong một số trò chơi đơn giản
- Bài tập cuối chương 6
-
Chương 7 Phương trình bậc nhất một ẩn
-
Chương 8 Tam giác đồng dạng. Hình đồng dạng
- Bài 1. Định lí Thalès trong tam giác
- Bài 2. Ứng dụng của định lí Thalès trong tam giác
- Bài 3. Đường trung bình của tam giác
- Bài 4. Tính chất đường phân giác của tam giác
- Bài 5. Tam giác đồng dạng
- Bài 6. Trường hợp đồng dạng thứ nhất của tam giác
- Bài 7. Trường hợp đồng dạng thứ hai của tam giác
- Bài 8. Trường hợp đồng dạng thứ ba của tam giác
- Bài 9. Hình đồng dạng
- Bài 10. Hình đồng dạng trong thực tiễn
- Bài tập cuối chương 8
-
Giải bài 12 trang 121 SGK Toán 8 tập 1 - Cánh diều
Cho hình thoi ABCD và
Đề bài
Cho hình thoi ABCD và hình bình hành BCMD. Gọi O là giao điểm của AC và BD. Chứng minh:
a) \(O{\rm{D}} = \frac{1}{2}CM\) và tam giác ACM là tam giác vuông.
b) Ba điểm A, D, M thẳng hàng.
c) Tam giác DCM là tam giác cân
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng tính chất của hình bình hành BCMD và hình thoi ABCD
- Tính chất hình bình hành
+ Các cạnh đối bằng nhau
+ Các góc đối bằng nhau
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường
- Tính chất hình thoi
+ Hai đường chéo vuông góc với nhau.
+ Hai đường chéo là các đường phân giác của các góc trong hình thoi.
Lời giải chi tiết
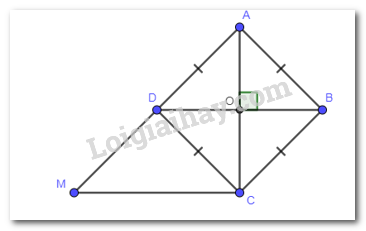
a) Vì BCMD là hình bình hành
Suy ra: BD = CM (1)
Mà ABCD là hình thoi
O là giao điểm của AC và BD
\( \Rightarrow O{\rm{D}} = \frac{1}{2}B{\rm{D}}(2)\)
Từ (1) và (2) suy ra: \(O{\rm{D}} = \frac{1}{2}CM\)
Vì BCMD là hình bình hành nên BD // CM (3)
Vì ABCD là hình thoi nên \(B{\rm{D}} \bot AC(4)\)
Từ (3), (4) suy ra: \(AC \bot CM\)
Suy ra: tam giác ACM là tam giác vuông tại C
b) ta có: AD // BC (vì ABCD là hình thoi)
DM // BC (vì DBCM là hình bình hành)
Suy ra A, D, M thẳng hàng
c) Ta có:BC = DC (vì ABCD là hình thoi)
DM = BC (vì DBCM là hình bình hành)
Suy ra: DM = DC
Suy ra tam giác DCM là tam giác cân tại D
Bình luận
Chia sẻ
- Giải bài 13 trang 121 SGK Toán 8 tập 1 - Cánh diều
- Giải bài 11 trang 121 SGK Toán 8 tập 1 - Cánh diều
- Giải bài 10 trang 121 SGK Toán 8 tập 1 - Cánh diều
- Giải bài 9 trang 121 SGK Toán 8 tập 1 - Cánh diều
- Giải bài 8 trang 121 SGK Toán 8 tập 1 - Cánh diều
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Cánh diều - Xem ngay
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
