Giải bài 10 trang 74 sách bài tập toán 9 - Chân trời sáng tạo tập 1

Cho tam giác OAB vuông tại O có OA = 8 cm, OB = 15 cm. a) (tan A = frac{{15}}{8}) b) (sin B = frac{{15}}{{17}}) c) (sin A = frac{8}{{17}}) d) cot A = tan B

Tổng hợp đề thi học kì 1 lớp 9 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - KHTN - Lịch sử và Địa lí

Đề bài

Chọn đúng hoặc sai cho mỗi ý a), b), c), d).

Cho tam giác OAB vuông tại O có OA = 8 cm, OB = 15 cm.

a) \(\tan A = \frac{{15}}{8}\)

b) \(\sin B = \frac{{15}}{{17}}\)

c) \(\sin A = \frac{8}{{17}}\)

d) cot A = tan B

Phương pháp giải - Xem chi tiết

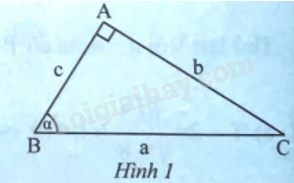
Dựa vào: Tam giác vuông ABC trong Hình 1, ta có:

\(\sin \alpha = \frac{{AC}}{{BC}} = \frac{b}{a};\cos \alpha = \frac{{AB}}{{BC}} = \frac{c}{a};\tan \alpha = \frac{{AC}}{{AB}} = \frac{b}{c};\cot \alpha = \frac{{AB}}{{AC}} = \frac{c}{b}.\)

Chú ý: Với góc nhọn \(\alpha \), ta có:

0 < sin \(\alpha \) < 1; 0 < cos \(\alpha \)< 1.

cot \(\alpha \) = \(\frac{1}{{\tan \alpha }}\)

Lời giải chi tiết

a) Đúng vì \(\tan A = \frac{{OB}}{{OA}} = \frac{{15}}{8}\).

b) Sai vì \(AB = \sqrt {O{A^2} + O{B^2}} = \sqrt {{8^2} + {{15}^2}} = 17\)

Suy ra sin B = \(\frac{{OA}}{{AB}} = \frac{8}{{17}}\).

c) Sai vì sin A = \(\frac{{OB}}{{AB}} = \frac{{15}}{{17}}\).

d) Đúng vì cot A = \(\frac{{OA}}{{OB}} = \frac{8}{{15}}\) và tan B = \(\frac{{OA}}{{OB}} = \frac{8}{{15}}\).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 11 trang 74 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Tam giác ABC vuông tại A, có AB = 24 cm, BC = 25 cm, AH là đường cao (Hình 5). a) AC = 8 cm b) (widehat B approx {16,26^o}) c) ({rm{cosC = }}frac{{24}}{{25}}) D. (AH approx 7)
Giải bài 12 trang 74 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Từ điểm A trên đỉnh một toà nhà cao 30 m, một người nhìn thấy một ô tô đang dừng tại vị trí B dưới một góc nghiêng xuống là 55o (Hình 6). a) (OB approx 21m) b) (AB = 47m) c) (widehat {{rm{OAB}}}{rm{ = }}{35^o}) D. (widehat {{rm{OBA}}}{rm{ = }}{35^o})
Giải bài 13 trang 74 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Cho tam giác ABC vuông tại A có đường cao AH, BH = 1 cm, CH = 4 cm. Giải tam giác ABC.
Giải bài 14 trang 74 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Giải các tam giác vuông trong Hình 7.
Giải bài 15 trang 75 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Cho tam giác ABC có AB = 15 cm, BC = 20 cm, (widehat {ABC} = {64^o}). Tính độ dài: a) đường cao AH; b) các đoạn thẳng BH, CH; c) cạnh AC
Giải bài 16 trang 75 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Một người đứng cách thân một cái quạt gió 16 m và nhìn thấy tâm của cánh quạt với góc nâng 56,5o . Tính khoảng cách từ tâm của cánh quạt đến mặt đất, biết khoảng cách từ mắt của người đó đến mặt đất là 1,5 m.
Giải bài 17 trang 75 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Một du khách đếm được 645 bước chân khi đi từ ngay dưới chân toàn tháp thẳng ra phía ngoài cho đến vị trí có góc nhìn lên đỉnh là 45o (Hình 9). Tính chiều cao của tháp, biết rằng khoảng cách trung bình của mỗi bước chân là 0,4 m.
Giải bài 18 trang 75 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Một người đứng trên một tháp hải đăng ở vị trí cao 75 m so với mặt nước biển đã quan sát hai lần thấy một chiếc thuyền đang hướng về phía tháp hải đăng với góc hạ lần lượt là 30o và 45o (Hình 10). Hỏi thuyền đi được bao nhiêu mét giữa hai lần quan sát?
Giải bài 9 trang 74 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Giá trị của biểu thức C = sin 75o – cos 15o + sin 30o là A. (frac{{sqrt 3 }}{2}) B. (frac{1}{2}) C. (frac{{sqrt 2 }}{2}) D. 0
Giải bài 8 trang 74 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Độ dài y trong Hình 4 (kết quả làm tròn đến hàng phần mười) là A. 10,2 B. 8,4 C. 10,3 D. 11
Giải bài 7 trang 73 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Khoảng cách giữa hai chân tháp AB và MN là x (Hình 3). So với phương nằm ngang AH, từ đỉnh A của tháp AB nhìn lên đỉnh M của tháp MN ta được góc (alpha ), từ đỉnh A của tháp AB nhìn xuống chân N của tháp MN ta được góc (beta ). Cho biết x = 120 m, (alpha ) = 30o và (beta ) = 20o . Chiều cao của tháp MN (kết quả làm tròn đến hàng đơn vị của mét) là A. 113 m B. 25 m C. 101 m D. 21,7 m
Giải bài 6 trang 73 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Một cầu trượt trong công viên có độ dốc là 28o và có độ cao là 2,1 m. Độ dài của mặt cầu trượt (kết quả làm tròn đến hàng phần mười) là A. 6,8 m B. 4,5 m C. 3,9 m D. 3,3 m
Giải bài 4 trang 73 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Số đo góc C trong Hình 1 (kết quả làm tròn đến hằng phần trăm của độ) là A. ({59,04^o}) B. ({30,93^o}) C. ({36,87^o}) D. ({53,13^o})
Giải bài 5 trang 73 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Độ dài cạnh BC trong Hình 2 (kết quả làm tròn đến hàng phần trăm) là A. 17,14 B. 9,83 C. 8,40 D. 6,88
Giải bài 3 trang 73 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Tỉ số lượng giác bằng với cos 58o là A. sin 58o B. sin 32o C. tan 32o D. cot 32o
Giải bài 2 trang 73 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Giá trị của biểu thức B = tan 45o .cos 30o. cot 30o là A. (frac{{sqrt 3 }}{3}) B. (frac{{sqrt 6 }}{2}) C. (frac{{sqrt 3 }}{2}) D. (frac{3}{2})
Giải bài 1 trang 73 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Cho tam giác ABC vuông tại A, có AB = 6 cm, AC = 8 cm. Giá trị của sin B là A. (frac{3}{4}) B. (frac{3}{5}) C. (frac{4}{5}) D. (frac{5}{4})