Đề thi giữa kì 1 Toán 8 - Đề số 6
Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:
Đề bài
Biểu thức nào sau đây là đa thức?
-
A.
\(\frac{{x + 2y}}{3}\).
-
B.
\(x + \frac{1}{y}\).
-
C.
\( - x + \frac{2}{x}y - 3{y^2}\).
-
D.
\(\frac{1}{{2x}} + {y^2}\).
Cặp đơn thức nào dưới đây là hai đơn thức đồng dạng?
-
A.
\(12{x^4}{y^4}\) và \(12{x^4}{y^6}\).
-
B.
\( - 12{x^4}{y^4}\) và \(12{x^6}{y^6}\).
-
C.
\(12{x^6}{y^4}\) và \( - 2{x^6}{y^4}\).
-
D.
\(12{x^4}{y^6}\) và \(12{x^6}{y^6}\).
Đa thức \(7{x^3}{y^2}z - 2{x^4}{y^3}\) chia hết cho đơn thức nào dưới đây?
-
A.
\(3{x^4}\).
-
B.
\( - 3{x^4}\).
-
C.
\( - 2{x^3}y\).
-
D.
\(2x{y^3}\).
Kết quả của phép nhân \(\left( {{x^2} - 2x + 1} \right)\left( {x - 1} \right)\) là
-
A.
\({x^3} - 3{x^2} + 3x - 1\).
-
B.
\({x^3} + 3{x^2} + 3x - 1\).
-
C.
\({x^3} - 3{x^2} + 3x + 1\).
-
D.
\({x^3} + 3{x^2} + 3x + 1\).
Kết quả của biểu thức \({\left( {x + 2} \right)^2} - 4\left( {x + 2} \right) + 4\) là
-
A.
\({x^2} + 16\).
-
B.
\({x^2} + 8x + 16\).
-
C.
\({x^2} - 4x\).
-
D.
\({x^2}\).
Đa thức \(14{x^2}y - 21x{y^2} + 28{x^2}{y^2}\) được phân tích thành
-
A.
\(7xy\left( {2x - 3y + 4xy} \right)\).
-
B.
\(xy\left( {14x - 21y + 28xy} \right)\).
-
C.
\(7{x^2}y\left( {2 - 3y + 4xy} \right)\).
-
D.
\(7x{y^2}\left( {2x - 3y + 4x} \right)\).
Biểu thức nào sau đây không phải là phân thức đại số?
-
A.
\(\frac{1}{x}\).
-
B.
\(x\).
-
C.
\(\frac{0}{x}\).
-
D.
\(\frac{x}{0}\).
Phân thức nào sau đây không phải là phân thức đối của phân thức \(\frac{{1 - x}}{x}\)?
-
A.
\(\frac{{x + 1}}{x}\).
-
B.
\(\frac{{ - \left( {1 - x} \right)}}{x}\).
-
C.
\( - \frac{{1 - x}}{x}\).
-
D.
\(\frac{{x - 1}}{x}\).
Khẳng định nào sau đây sai về hình chóp tam giác đều \(S.ABC?\)
-
A.
Đáy \(ABC\) là tam giác đều.
-
B.
\(SA = SB = SC\).
-
C.
Tam giác \(SBC\) là tam giác đều.
-
D.
\(\Delta SAB = \Delta SBC = \Delta SCA\).
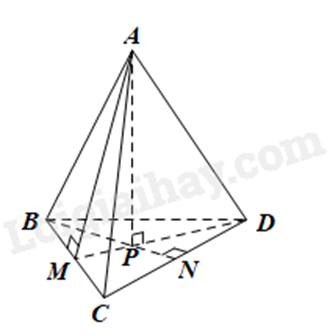
Cho hình chóp tam giác đều \(A.BCD\) như hình vẽ bên. Đoạn thẳng nào sau đây là trung đoạn của hình chóp?
-
A.
\(AC\).
-
B.
\(AM\).
-
C.
\(BN\).
-
D.
\(AP\).
Cho tam giác \(ABC\) vuông có cạnh huyền \(AB = \sqrt {117} \;\;{\rm{cm,}}\,\,BC = 6\;\;{\rm{cm}}.\) Gọi \(K\) là trung điểm của đoạn thẳng \(AC\). Độ dài \(BK\) là
-
A.
\(3\;\;{\rm{cm}}\).
-
B.
\(4,5\;\;{\rm{cm}}\).
-
C.
\(7,5\;\;{\rm{cm}}\).
-
D.
\(10\;\;{\rm{cm}}\).
Cho tứ giác \(ABCD\). Khẳng định nào sau đây là sai?
-
A.
\(AB\) và \(BC\) là hai cạnh kề nhau.
-
B.
\(BC\) và \(AD\) là hai cạnh đối nhau.
-
C.
\(\widehat A\) và \(\widehat B\) là hai góc đối nhau.
-
D.
\(AC\) và \(BD\) là hai đường chéo.
Lời giải và đáp án
Biểu thức nào sau đây là đa thức?
-
A.
\(\frac{{x + 2y}}{3}\).
-
B.
\(x + \frac{1}{y}\).
-
C.
\( - x + \frac{2}{x}y - 3{y^2}\).
-
D.
\(\frac{1}{{2x}} + {y^2}\).
Đáp án : A
Dựa vào khái niệm đa thức: Đa thức là một tổng của những đơn thức.
Biểu thức \(\frac{{x + 2y}}{3} = \frac{1}{3}x + \frac{2}{3}y\) là đa thức.
Biểu thức \(x + \frac{1}{y}\) không phải là đa thức vì \(\frac{1}{y}\) không phải đơn thức.
Biểu thức \( - x + \frac{2}{x}y - 3{y^2}\) không phải là đa thức vì \(\frac{2}{x}y\) không phải đơn thức.
Biểu thức \(\frac{1}{{2x}} + {y^2}\) không phải là đa thức vì \(\frac{1}{{2x}}\) không phải đơn thức.
Đáp án A.
Cặp đơn thức nào dưới đây là hai đơn thức đồng dạng?
-
A.
\(12{x^4}{y^4}\) và \(12{x^4}{y^6}\).
-
B.
\( - 12{x^4}{y^4}\) và \(12{x^6}{y^6}\).
-
C.
\(12{x^6}{y^4}\) và \( - 2{x^6}{y^4}\).
-
D.
\(12{x^4}{y^6}\) và \(12{x^6}{y^6}\).
Đáp án : C
Hai đơn thức đồng dạng là hai đơn thức có hệ số khác 0 và có cùng phần biến.
Hai đơn thức \(12{x^6}{y^4}\) và \( - 2{x^6}{y^4}\) là hai đơn thức đồng dạng vì cùng có hệ số khác 0 và cùng phần biến \({x^6}{y^4}\).
Đáp án C.
Đa thức \(7{x^3}{y^2}z - 2{x^4}{y^3}\) chia hết cho đơn thức nào dưới đây?
-
A.
\(3{x^4}\).
-
B.
\( - 3{x^4}\).
-
C.
\( - 2{x^3}y\).
-
D.
\(2x{y^3}\).
Đáp án : C
Đa thức chia hết cho đơn thức nếu mọi hạng tử của đa thức chia hết cho đơn thức đó.
Đa thức \(7{x^3}{y^2}z - 2{x^4}{y^3}\) chia hết cho \( - 2{x^3}y\).
Hạng tử \(7{x^3}{y^2}z\) không chia hết cho đơn thức \(3{x^4}\), \( - 3{x^4}\) và \(2x{y^3}\) nên đa thức \(7{x^3}{y^2}z - 2{x^4}{y^3}\) cũng không chia hết cho \(3{x^4}\), \( - 3{x^4}\) và \(2x{y^3}\).
Đáp án C.
Kết quả của phép nhân \(\left( {{x^2} - 2x + 1} \right)\left( {x - 1} \right)\) là
-
A.
\({x^3} - 3{x^2} + 3x - 1\).
-
B.
\({x^3} + 3{x^2} + 3x - 1\).
-
C.
\({x^3} - 3{x^2} + 3x + 1\).
-
D.
\({x^3} + 3{x^2} + 3x + 1\).
Đáp án : A
Sử dụng hằng đẳng thức bình phương của một hiệu \({\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\) và lập phương của một hiệu \({\left( {A - B} \right)^3} = {A^3} - 3{A^2}B + 3A{B^2} - {B^3}\).
Ta có:
\(\left( {{x^2} - 2x + 1} \right)\left( {x - 1} \right) = {\left( {x - 1} \right)^2}\left( {x - 1} \right) = {\left( {x - 1} \right)^3} = {x^3} - 3{x^2} + 3x - 1\).
Đáp án A.
Kết quả của biểu thức \({\left( {x + 2} \right)^2} - 4\left( {x + 2} \right) + 4\) là
-
A.
\({x^2} + 16\).
-
B.
\({x^2} + 8x + 16\).
-
C.
\({x^2} - 4x\).
-
D.
\({x^2}\).
Đáp án : D
Sử dụng hằng đẳng thức bình phương của một hiệu \({\left( {A - B} \right)^2} = {A^2} - 2AB + {B^2}\).
Ta có:
\({\left( {x + 2} \right)^2} - 4\left( {x + 2} \right) + 4 = {\left( {x + 2 - 2} \right)^2} = {x^2}.\)
Đáp án D.
Đa thức \(14{x^2}y - 21x{y^2} + 28{x^2}{y^2}\) được phân tích thành
-
A.
\(7xy\left( {2x - 3y + 4xy} \right)\).
-
B.
\(xy\left( {14x - 21y + 28xy} \right)\).
-
C.
\(7{x^2}y\left( {2 - 3y + 4xy} \right)\).
-
D.
\(7x{y^2}\left( {2x - 3y + 4x} \right)\).
Đáp án : A
Sử dụng phương pháp đặt nhân tử chung để phân tích đa thức thành nhân tử.
Ta có:
\(14{x^2}y - 21x{y^2} + 28{x^2}{y^2} = 7xy\left( {2x - 3y + 4xy} \right)\).
Đáp án A.
Biểu thức nào sau đây không phải là phân thức đại số?
-
A.
\(\frac{1}{x}\).
-
B.
\(x\).
-
C.
\(\frac{0}{x}\).
-
D.
\(\frac{x}{0}\).
Đáp án : D
Phân thức đại số là biểu thức có dạng \(\frac{P}{Q}\), trong đó P, Q là các đa thức và Q khác đa thức 0.
Biểu thức \(\frac{x}{0}\) không phải là phân thức đại số vì có mẫu thức bằng 0.
Đáp án D.
Phân thức nào sau đây không phải là phân thức đối của phân thức \(\frac{{1 - x}}{x}\)?
-
A.
\(\frac{{x + 1}}{x}\).
-
B.
\(\frac{{ - \left( {1 - x} \right)}}{x}\).
-
C.
\( - \frac{{1 - x}}{x}\).
-
D.
\(\frac{{x - 1}}{x}\).
Đáp án : A
Phân thức đối của phân thức \(\frac{A}{B}\) là phân thức \( - \frac{A}{B}\).
Sử dụng kiến thức về tính chất của phân thức để tìm các phân thức bằng phân thức đối.
Phân thức đối của phân thức \(\frac{{1 - x}}{x}\) là \( - \frac{{1 - x}}{x} = \frac{{ - \left( {1 - x} \right)}}{x} = \frac{{x - 1}}{x}\)
Vậy phương án A là sai.
Đáp án A.
Khẳng định nào sau đây sai về hình chóp tam giác đều \(S.ABC?\)
-
A.
Đáy \(ABC\) là tam giác đều.
-
B.
\(SA = SB = SC\).
-
C.
Tam giác \(SBC\) là tam giác đều.
-
D.
\(\Delta SAB = \Delta SBC = \Delta SCA\).
Đáp án : C
Dựa vào đặc điểm của hình chóp tam giác đều.
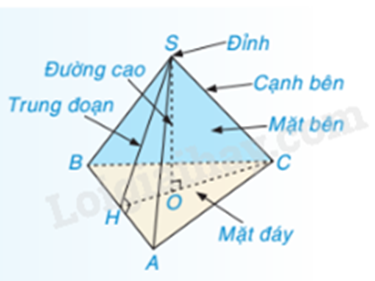
Hình chóp tam giác đều \(S.ABC\) có mặt bên là các tam giác cân nên \(\Delta SBC\) là tam giác cân.
Do đó khẳng định C sai.
Đáp án C.
Cho hình chóp tam giác đều \(A.BCD\) như hình vẽ bên. Đoạn thẳng nào sau đây là trung đoạn của hình chóp?

-
A.
\(AC\).
-
B.
\(AM\).
-
C.
\(BN\).
-
D.
\(AP\).
Đáp án : B
Trung đoạn là đoạn thẳng vuông góc kẻ từ tâm của một đa giác đều xuống cạnh đáy của nó.
Trung đoạn của hình chóp \(A.BCD\) là đoạn thẳng \(AM\).
Đáp án B.
Cho tam giác \(ABC\) vuông có cạnh huyền \(AB = \sqrt {117} \;\;{\rm{cm,}}\,\,BC = 6\;\;{\rm{cm}}.\) Gọi \(K\) là trung điểm của đoạn thẳng \(AC\). Độ dài \(BK\) là
-
A.
\(3\;\;{\rm{cm}}\).
-
B.
\(4,5\;\;{\rm{cm}}\).
-
C.
\(7,5\;\;{\rm{cm}}\).
-
D.
\(10\;\;{\rm{cm}}\).
Đáp án : C
Áp dụng định lí Pythagore vào tam giác ABC để tính AC.
Tính độ dài CK.
Áp dụng định lí Pythagore vào tam giác BCK để tính BK.
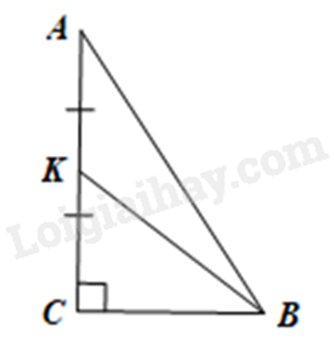
Xét \(\Delta ABC\) vuông tại \(C\), theo định lí Pythagore ta có:
\(A{C^2} = A{B^2} - B{C^2} = {\left( {\sqrt {117} } \right)^2} - {6^2} = 81\)
Suy ra \(AC = \sqrt {81} = 9\;\;{\rm{cm}}\)
Do \(K\) là trung điểm của đoạn thẳng \(AC\) nên \(CK = \frac{1}{2}AC = 4,5\;\;{\rm{cm}}\)
Xét \(\Delta BCK\) vuông tại \(C\), theo định lí Pythagore ta có:
\(B{K^2} = B{C^2} + C{K^2} = {6^2} + 4,{5^2} = 56,25\)
Suy ra \(BK = \sqrt {56,25} = 7,5\;\;{\rm{cm}}\).
Đáp án C.
Cho tứ giác \(ABCD\). Khẳng định nào sau đây là sai?
-
A.
\(AB\) và \(BC\) là hai cạnh kề nhau.
-
B.
\(BC\) và \(AD\) là hai cạnh đối nhau.
-
C.
\(\widehat A\) và \(\widehat B\) là hai góc đối nhau.
-
D.
\(AC\) và \(BD\) là hai đường chéo.
Đáp án : C
Dựa vào kiến thức về tứ giác.
Tứ giác \(ABCD\) có các cặp góc đối nhau là \(\widehat {A\,\,}\) và \(\widehat {C\,};\) \(\widehat {B\,}\) và \(\widehat {D\,}\).
Do đó phương án C là khẳng định sai.
Đáp án C.
a) Sử dụng quy tắc chia đa thức cho đơn thức: Muốn chia đa thức A cho đơn thức B (trường hợp chia hết), ta chia từng hạng tử của A cho B rồi cộng các kết quả với nhau.
b) Sử dụng quy tắc nhân đơn thức với đa thức: Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau.
a) \(\left( { - 9{x^2}{y^3} + 6{x^3}{y^2} - 4x{y^2}} \right):3x{y^2}\)
\( = - 9{x^2}{y^3}:3x{y^2} + 6{x^3}{y^2}:3x{y^2} - 4x{y^2}:3x{y^2}\)
\( = - 3xy + 2{x^2} - \frac{4}{3}.\)
b) \(\frac{1}{2}xy\left( {{x^5} - {y^3}} \right) - {x^2}y\left( {\frac{1}{4}{x^4} - {y^3}} \right)\)
\( = \frac{1}{2}xy \cdot {x^5} + \frac{1}{2}xy \cdot \left( { - {y^3}} \right) - {x^2}y \cdot \frac{1}{4}{x^4} - {x^2}y \cdot \left( { - {y^3}} \right)\)
\( = \frac{1}{2}{x^6}y - \frac{1}{2}x{y^4} - \frac{1}{4}{x^6}y + {x^2}{y^4}\)
\( = \left( {\frac{1}{2}{x^6}y - \frac{1}{4}{x^6}y} \right) - \frac{1}{2}x{y^4} + {x^2}{y^4}\)
\( = \frac{1}{4}{x^6}y - \frac{1}{2}x{y^4} + {x^2}{y^4}\).
Sử dụng các quy tắc phân tích đa thức thành nhân tử.
a) \(3x\left( {3 - x} \right) - 6\left( {x - 3} \right)\)
\( = 3x\left( {3 - x} \right) + 6\left( {3 - x} \right)\)
\( = \left( {3 - x} \right)\left( {3x + 6} \right)\)
\( = 3\left( {3 - x} \right)\left( {x + 2} \right).\)
b) \({\left( {{x^2} + 1} \right)^2} - 4{x^2}\)
\( = {\left( {{x^2} + 1} \right)^2} - {\left( {2x} \right)^2}\)
\( = \left( {{x^2} + 1 - 2x} \right)\left( {{x^2} + 1 + 2x} \right)\)
\( = {\left( {x - 1} \right)^2}{\left( {x + 1} \right)^2}.\)
c) \({x^6} + {x^3} - {x^2} - 1\)
\( = \left( {{x^6} + {x^3}} \right) - \left( {{x^2} + 1} \right)\)
\( = {x^3}\left( {{x^2} + 1} \right) - \left( {{x^2} + 1} \right)\)
\( = \left( {{x^2} + 1} \right)\left( {{x^3} - 1} \right)\)
\( = \left( {{x^2} + 1} \right)\left( {x - 1} \right)\left( {{x^2} + x + 1} \right).\)
a) Quy đồng mẫu thức để rút gọn biểu thức.
b) Thay \(x = 4\) vào \(A\) để tính giá trị.
c) Ta biến đổi để đưa A về dạng \(A = m + \frac{a}{B}\) với m và a là số nguyên.
Khi đó A có giá trị nguyên khi \(a \vdots B\) hay \(B \in \) Ư(a).
a) Với \(x \ne \pm 2\), ta có:
\(A = \frac{{x + 1}}{{x - 2}} + \frac{{x - 1}}{{x + 2}} + \frac{{{x^2} + 4x}}{{4 - {x^2}}}\)
\( = \frac{{x + 1}}{{x - 2}} + \frac{{x - 1}}{{x + 2}} - \frac{{{x^2} + 4x}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}\)
\( = \frac{{\left( {x + 1} \right)\left( {x + 2} \right)}}{{\left( {x - 2} \right)\left( {x + 2} \right)}} + \frac{{\left( {x - 1} \right)\left( {x - 2} \right)}}{{\left( {x - 2} \right)\left( {x + 2} \right)}} - \frac{{{x^2} + 4x}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}\)
\( = \frac{{{x^2} + 3x + 2 + {x^2} - 3x + 2 - {x^2} - 4x}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}\)
\( = \frac{{{x^2} - 4x + 4}}{{\left( {x - 2} \right)\left( {x + 2} \right)}} = \frac{{{{\left( {x - 2} \right)}^2}}}{{\left( {x - 2} \right)\left( {x + 2} \right)}} = \frac{{x - 2}}{{x + 2}}\).
Vậy với \(x \ne \pm 2\) ta có \(A = \frac{{x - 2}}{{x + 2}}.\)
b) Thay \(x = 4\) (thỏa mãn) vào biểu thức \(A\) ta có: \(A = \frac{{4 - 2}}{{4 + 2}} = \frac{2}{6} = \frac{1}{3}.\)
c) Với \(x \ne \pm 2\) và \(x \in \mathbb{Z}\) ta có: \(A = \frac{{x - 2}}{{x + 2}} = \frac{{x + 2 - 4}}{{x + 2}} = 1 - \frac{4}{{x + 2}}\)
Ta có \(1 \in \mathbb{Z}\) nên để \(A = 1 - \frac{4}{{x + 2}}\) nhận giá trị nguyên thì \(\frac{4}{{x + 2}} \in \mathbb{Z}\),
suy ra \(4 \vdots \left( {x + 2} \right)\)
hay \(\left( {x + 2} \right) \in \)Ư\(\left( 4 \right) = \left\{ { \pm 1; \pm 2; \pm 4} \right\}\)
Ta có bảng sau:
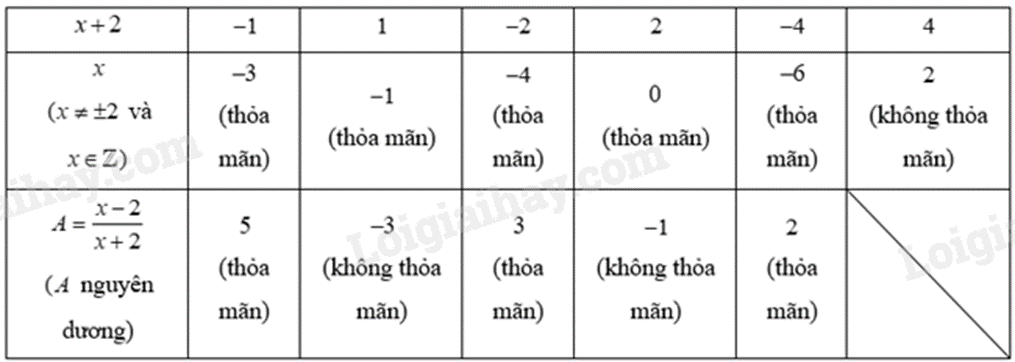
Vậy \(x \in \left\{ { - 3; - 4; - 6} \right\}.\)
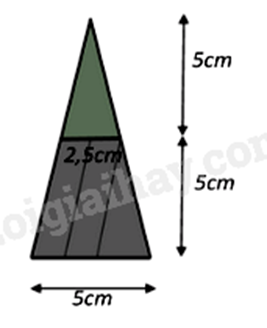
Sử dụng công thức tính thể tích của hình chóp tứ giác: \(V = \frac{1}{3}.{S_{đáy}}.h\).
Biết \(1c{m^3} = 1ml\).
a) Thể tích của lọ nước hoa hình kim tự tháp là:
\({V_1} = \frac{1}{3} \cdot {5^2} \cdot \left( {5 + 5} \right) = \frac{{250}}{3}\;\;\left( {{\rm{c}}{{\rm{m}}^3}} \right).\)
b) Thể tích của nắp lọ nước hoa là:
\({V_1} = \frac{1}{3} \cdot 2,{5^2} \cdot 5 = \frac{{125}}{{12}}\;\;\left( {{\rm{c}}{{\rm{m}}^3}} \right).\)
Dung tích của lọ nước hoa đó là:
\(\frac{{250}}{3} - \frac{{125}}{{12}} \approx 73\;\;{\rm{c}}{{\rm{m}}^3} = 73\,\,ml\).
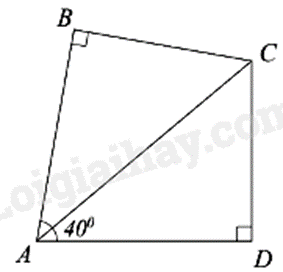
a) Dựa vào tính chất của tia phân giác để tính góc BAD.
Sử dụng định lí tổng các góc của một tứ giác bẳng \(360^\circ \) để tính góc BCD.
b) Sử dụng định lí Pythagore để tính AC.
Dựa vào kiến thức: quãng đường = vận tốc . thời gian để tính vận tốc của vận động viên.
a) Do \(AC\) là tia phân giác \(\widehat {BAD}\) nên ta có \(\widehat {BAD} = 2\widehat {DAC} = 2 \cdot 40^\circ = 80^\circ \)
Xét tứ giác \(ABCD\) có: \(\widehat {BAD} + \widehat {B\,} + \widehat {BCD} + \widehat {D\,} = 360^\circ \)
Suy ra
\(\widehat {BCD} = 360^\circ - \left( {\widehat {BAD} + \widehat {B\,} + \widehat {D\,}} \right) \\= 360^\circ - \left( {80^\circ - 90^\circ - 90^\circ } \right) = 100^\circ \)
b) Xét \(\Delta ABC\) vuông tại \(B\), theo định lí Pythagore ta có:
\(A{C^2} = A{B^2} + B{C^2} = 7,{66^2} + 6,{43^2} = 100,0205\)
Suy ra \(AC = \sqrt {100,0205} \approx 10,0\) m.
Khi đó vận động viên cần bơi với vận tốc là \(\frac{{10,0}}{{20}} = 0,5\) (m/s).
Sử dụng hằng đẳng thức bình phương của một tổng, hiệu hai bình phương.
Dựa vào kiến thức \(A.B \le 0\) thì A và B trái dấu để tìm giá trị lớn nhất và nhỏ nhất của P.
Ta có: \({x^2} + 2xy + 6x + 6y + 2{y^2} + 8 = 0\)
\(\left( {{x^2} + 2xy + {y^2}} \right) + 6\left( {x + y} \right) + 9 + {y^2} - 1 = 0\)
\({\left( {x + y} \right)^2} + 6\left( {x + y} \right) + 9 - 1 = - {y^2}\)
\({\left( {x + y + 3} \right)^2} - 1 = - {y^2}\)
\(\left( {x + y + 3 - 1} \right)\left( {x + y + 3 + 1} \right) = - {y^2}\)
\(\left( {x + y + 2} \right)\left( {x + y + 4} \right) = - {y^2}\)
\(\left( {x + y + 2024 - 2022} \right)\left( {x + y + 2024 - 2020} \right) = - {y^2}\)
\(\left( {P - 2022} \right)\left( {P - 2020} \right) = - {y^2}\)
\(\left( {P - 2022} \right)\left( {P - 2020} \right) = - {y^2}\)
Mà \({y^2} \ge 0\) nên \( - {y^2} \le 0\) với mọi \(y\)
Do đó \(\left( {P - 2022} \right)\left( {P - 2020} \right) \le 0\) \(\left( * \right)\)
Lại có \(\left( {P - 2020} \right) - 2 < P - 2020\) hay \(P - 2022 < P - 2020\)
Suy ra \(\left( * \right)\) xảy ra khi \(P - 2022 \le 0 \le P - 2020\)
Nên \(2020 \le P \le 2022\)
Vậy GTLN của \(P\) bằng 2022 khi \(\left\{ \begin{array}{l}x + y + 2 = 0\\ - {y^2} = 0\end{array} \right.\), tức \(\left\{ \begin{array}{l}x = - 2\\y = 0\end{array} \right.\);
GTNN của \(P\) bằng 2020 khi \(\left\{ \begin{array}{l}x + y + 4 = 0\\ - {y^2} = 0\end{array} \right.\), tức \(\left\{ \begin{array}{l}x = - 4\\y = 0\end{array} \right.\).
Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:
Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:
Câu 1: Kết quả của phép nhân đa thức (4{{rm{x}}^5} + 7{{rm{x}}^2}) với đơn thức ( - 3{{rm{x}}^3}) là :
Câu 1: Trong các biểu thức sau, biểu thức nào không phải đơn thức?
Câu 1: Cho các biểu thức ({x^2} - 2 + 4x{y^2};frac{x}{y} + 2{y^2};2023;x(x - y)). Có bao nhiêu đa thức trong các biểu thức trên?
Câu 1: Cho các biểu thức (2x + y + {x^2}y; - 3x{y^2}{z^3} + frac{1}{2}{x^2}{y^2}z;frac{{x + y}}{{x - y}}). Có bao nhiêu đa thức trong các biểu thức trên?
Câu 1: Tìm hệ số trong đơn thức ( - 36{a^2}{b^2}{x^2}{y^3}) với a,b là hằng số.
>> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
 |
 |
 |
 |
 |
 |










Bình luận