Đề số 21 - Đề thi vào lớp 10 môn Toán

Đề bài

Câu 1. (2,0 điểm)

1. Giải các phương trình sau:

a) $5\left( {x + 1} \right) = 3x + 7$               

b) ${x^4} - {x^2} - 12 = 0$

2. Cho hệ phương trình: $\left\{ \begin{array}{l}3x - y = 2m - 1\\x + 2y = 3m + 2\end{array} \right.$

a) Giải hệ phương trình khi $m = 1$              b) Tìm m để hệ có nghiệm $\left( {x;y} \right)$ thỏa mãn: ${x^2} + {y^2} = 10$

Câu 2. (1,5 điểm). Cho phương trình $A = \left( {\dfrac{1}{{x - \sqrt x }} + \dfrac{1}{{\sqrt x  - 1}}} \right):\dfrac{{\sqrt x  + 1}}{{{{\left( {\sqrt x  - 1} \right)}^2}}}$ (với $x > 0,x \ne 1$ )

a) Rút gọn biểu thức A.       

b) Tìm giá trị lớn nhất của biểu thức $P = A - 9\sqrt x$

Câu 3. (1,0 điểm). Một chiếc bè trôi từ bến sông A đến bên B với vận tốc dòng nước là 4km/h, cùng lúc đó một chiếc thuyền chạy từ bến A đến B rồi quay lại ngay thì gặp chiếc bè tại vị trí C cách bến A là 8km. Tính vận tốc thực của thuyền biết khoảng cách giữa hai bến A và B là 24 km.

Câu 4. (1.5 điểm). Trong hệ tọa độ Oxy, cho Parabol $y = {x^2}\left( P \right)$ và đường thẳng có phương trình $y = \left( {m - 1} \right)x + {m^2} - 2m + 3\left( d \right)$

a) Chứng minh với mọi giá trị của m thì (d) luôn cắt (P) tại hai điểm phân biệt.

b) Giả sử (d) cắt (P) tại hai điểm phân biệt A, B. Tìm m để tam giác OAB cân tại O. Khi đó tính diện tích tam giác OAB.

Câu 5. (3.0 điểm) Cho nửa đường tròn tâm O đường kính AB, M là một điểm bất kỳ thuộc nửa đường tròn (M khác A, B). Tiếp tuyến tại M cắt các tiếp tuyến Ax và By của nửa đường tròn đó lần lượt tại C và D.

a) Chứng minh: $\widehat {COD} = {90^0}$

b) Gọi K là giao điểm của BM với Ax. Chứng minh: $\Delta KMO \sim \Delta AMD$

c) Tìm giá trị nhỏ nhất của tổng diện tích hai tam giác ACM và BDM.

Câu 6. (1,0 điểm)

a) Cho hàm số $y = f\left( x \right)$  với $f\left( x \right)$ là một biểu thức đại số xác định với mọi số thực $x \ne 0$ . Biết rằng: $f\left( x \right) + 3f\left( {\dfrac{1}{x}} \right) = {x^2}\left( {\forall x \ne 0} \right).$ Tính $f\left( 2 \right)$

b) Cho ba số nguyên dương $a,b,c$ đôi một khác nhau và thỏa mãn: $a$ là ước của $b + c + bc$, $b$  là ước của $c + a + ca$  và $c$ là ước của $a + b + ab$ . Chứng minh $a,b,c$ không đồng thời là các số nguyên tố.

Lời giải chi tiết

Câu 1.

1. Giải các phương trình sau:

a)$5\left( {x + 1} \right) = 3x + 7$

$\begin{array}{l} \Leftrightarrow 5x - 3x = 7 - 5\\ \Leftrightarrow 2x = 2\\ \Leftrightarrow x = 1\end{array}$

b) ${x^4} - {x^2} - 12 = 0$  (1)

Đặt ${x^2} = t\,\,\left( {t \ge 0} \right)$ Khi đó phương trình (1) trở thành:

$\begin{array}{l}{t^2} - t - 12 = 0\\ \Leftrightarrow {t^2} + 3t - 4t - 12 = 0\\ \Leftrightarrow \left( {t + 3} \right)\left( {t - 4} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}t =  - 3\left( {ktm} \right)\\t = 4\left( {tm} \right)\end{array} \right.\end{array}$

Với $t = 4 \Leftrightarrow {x^2} = 4 \Leftrightarrow x =  \pm 2$

Vậy phương trình (1) có tập nghiệm là: $S = \left\{ { - 2;2} \right\}$

2) Cho hệ phương trình: $\left\{ \begin{array}{l}3x - y = 2m - 1\\x + 2y = 3m + 2\end{array} \right.$

a) Giải hệ phương trình khi $m = 1$

Thay m = 1 vào hệ phương trình ta được hệ phương trình mới:

$\left\{ \begin{array}{l}3x - y = 2.1 - 1\\x + 2y = 3.1 + 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x - y = 1\\x + 2y = 5\end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l}6x - 2y = 2\\x + 2y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 3x - 1\end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 2\end{array} \right.$

Vậy hệ phương trình đã cho có nghiệm là: $\left( {x;y} \right) = \left( {1;2} \right)$

b) Tìm m để hệ có nghiệm $\left( {x;y} \right)$ thỏa mãn: ${x^2} + {y^2} = 10$

Ta có: $\dfrac{3}{1} \ne \dfrac{{ - 1}}{2}$ nên hệ phương trình đã cho luôn có nghiệm $\left( {x;y} \right)$.

$\left\{ \begin{array}{l}3x - y = 2m - 1\\x + 2y = 3m + 2\end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l}y = 3x - 2m + 1\\x + 2\left( {3x - 2m + 1} \right) = 3m + 2\end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l}y = 3x - 2m + 1\\x + 6x - 4m + 2 - 3m - 2 = 0\end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l}y = 3x - 2m + 1\\x = m\end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l}y = m + 1\\x = m\end{array} \right.$

Theo đề bài ta có nghiệm $\left( {x;y} \right)$ thỏa mãn:

$\begin{array}{l}{x^2} + {y^2} = 10\\ \Leftrightarrow {m^2} + {\left( {m + 1} \right)^2} = 10\\ \Leftrightarrow 2{m^2} + 2m - 9 = 0\,\,\,\,\left( * \right)\end{array}$

$\Delta ' = 1 + 18 = 19 > 0$

Khi đó (*) luôn có 2 nghiệm phân biệt: $\left[ \begin{array}{l}m = \dfrac{{ - 1 - \sqrt {19} }}{2}\\m = \dfrac{{ - 1 + \sqrt {19} }}{2}\end{array} \right.$

Câu 2.

a) Rút gọn biểu thức A.

$A = \left( {\dfrac{1}{{x - \sqrt x }} + \dfrac{1}{{\sqrt x  - 1}}} \right):\dfrac{{\sqrt x  + 1}}{{{{\left( {\sqrt x  - 1} \right)}^2}}}$ (với $x > 0,x \ne 1$)

$\begin{array}{l}A = \left( {\dfrac{1}{{\sqrt x \left( {\sqrt x  - 1} \right)}} + \dfrac{{\sqrt x }}{{\sqrt x \left( {\sqrt x  - 1} \right)}}} \right):\dfrac{{\sqrt x  + 1}}{{{{\left( {\sqrt x  - 1} \right)}^2}}}\\ = \dfrac{{1 + \sqrt x }}{{\sqrt x \left( {\sqrt x  - 1} \right)}}.\dfrac{{{{\left( {\sqrt x  - 1} \right)}^2}}}{{\sqrt x  + 1}}\\ = \dfrac{{\sqrt x  - 1}}{{\sqrt x }}\end{array}$

b) Tìm giá trị lớn nhất của biểu thức $P = A - 9\sqrt x$

$\begin{array}{l}P = A - 9\sqrt x \\ = \dfrac{{\sqrt x  - 1}}{{\sqrt x }} - 9\sqrt x \\ = 1 - \left( {\dfrac{1}{{\sqrt x }} + 9\sqrt x } \right)\end{array}$

Với $x > 0,x \ne 1$, áp dụng bất đẳng thức Cosi cho hai số dương $\dfrac{1}{{\sqrt x }};9\sqrt x$ ta có: $\dfrac{1}{{\sqrt x }} + 9\sqrt x  \ge 2\sqrt {\dfrac{1}{{\sqrt x }}.9\sqrt x }  = 6$

Từ đó ta có: $1 - \left( {\dfrac{1}{{\sqrt x }} + 9\sqrt x } \right) \le 1 - 6 =  - 5$

Vậy giá trị lớn nhất của biểu thức P là -5. Dấu “= xảy ra khi và chỉ khi $\dfrac{1}{{\sqrt x }} = 9\sqrt x  \Leftrightarrow x = \dfrac{1}{9}$

Câu 3.

Một chiếc bè trôi từ bến sông A đến bên B với vận tốc dòng nước là 4km/h, cùng lúc đó một chiếc thuyền chạy từ bến A đến B rồi quay lại ngay thì gặp chiếc bè tại vị trí C cách bến A là 8km. Tính vận tốc thực của thuyền biết khoảng cách giữa hai bến A và B là 24 km.

Gọi vận tốc thực của thuyền là: $\left( {x > 4} \right)$

Vận tốc xuôi dòng của thuyền là: $x + 4\left( {km/h} \right)$

Vận tốc ngược dòng của thuyền là: $x - 4\left( {km/h} \right)$

Vì thuyền chạy từ A đến B rồi quay lại ngay thì gặp chiếc bè tại vị trị C cách bến A là 8km tức là thuyền đi xuôi dòng được 24 km và ngược dòng được 24 – 8 = 16 km, nên ta có thời gian của thuyền đi đến khi gặp chiếc bè là: $\dfrac{{24}}{{x + 4}} + \dfrac{{16}}{{x - 4}}\left( h \right)$

Thời gian của chiếc bè trôi đến khi gặp thuyền là: $8:4 = 2\left( h \right)$

Khi đó ta có phương trình:

 $\begin{array}{l}\dfrac{{24}}{{x + 4}} + \dfrac{{16}}{{x - 4}} = 2\\ \Leftrightarrow \dfrac{{24\left( {x - 4} \right) + 16\left( {x + 4} \right)}}{{{x^2} - 16}} = \dfrac{{2\left( {{x^2} - 16} \right)}}{{{x^2} - 16}}\\ \Leftrightarrow 24x - 96 + 16x + 64 = 2{x^2} - 32\\ \Leftrightarrow {x^2} - 20x = 0\\ \Leftrightarrow x\left( {x - 20} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\left( {ktm} \right)\\x = 20\left( {tm} \right)\end{array} \right.\end{array}$

Vậy vận tốc thực của thuyền là 20 km/h.

Câu 4.

Trong hệ tọa độ Oxy, cho Parabol $y = {x^2}\left( P \right)$ và đường thẳng có phương trình $y = \left( {m - 1} \right)x + {m^2} - 2m + 3\left( d \right)$

a) Chứng minh với mọi giá trị của m thì (d) luôn cắt (P) tại hai điểm phân biệt.

Phương trình hoành độ giao điểm của (P) và (d) là:

$\begin{array}{l}{x^2} = \left( {m - 1} \right)x + {m^2} - 2m + 3\\ \Leftrightarrow {x^2} - \left( {m - 1} \right)x - {m^2} + 2m - 3 = 0\,\,\,\,\left( 1 \right)\end{array}$

Số giao điểm của (P) và (d) chính là số nghiệm của phương trình (1). Ta có:

$\begin{array}{l}\Delta  = {\left( {m - 1} \right)^2} - 4\left( { - {m^2} + 2m - 3} \right)\\ = {m^2} - 2m + 1 + 4{m^2} - 8m + 12\\ = 5{m^2} - 10m + 13\\ = 5\left( {{m^2} - 2m + 1} \right) + 8\\ = 5{\left( {m - 1} \right)^2} + 8 > 0,\forall m\end{array}$

Vậy phương trình (1) luôn có hai nghiệm phân biệt. Nên (d) luôn cắt (P) tại hai điểm phân biệt.

b) Giả sử (d) cắt (P) tại hai điểm phân biệt A, B: $A\left( {{x_1};{y_1}} \right);B\left( {{x_2};{y_2}} \right),\left( {{x_1} \ne {x_2}} \right)$ mà A, B thuộc vào (P) nên $A\left( {{x_1};x_1^2} \right);B\left( {{x_2};x_2^2} \right)$

Áp dụng hệ thức Viet cho phương trình (1) ta có: $\left\{ \begin{array}{l}{x_1} + {x_2} = m - 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( * \right)\\{x_1}{x_2} =  - {m^2} + 2m - 3\,\,\,\left( {**} \right)\end{array} \right.$

Tam giác OAB cân tại O nên OA = OB hay $O{A^2} = O{B^2}$

$\begin{array}{l} \Leftrightarrow x_1^2 + {\left( {x_1^2} \right)^2} = x_2^2 + {\left( {x_2^2} \right)^2}\\ \Leftrightarrow x_1^2 + x_1^4 = x_2^2 + x_2^4\\ \Leftrightarrow \left( {x_1^2 - x_2^2} \right) + \left( {x_1^4 - x_2^4} \right) = 0\\ \Leftrightarrow \left( {x_1^2 - x_2^2} \right)\left( {1 + x_1^2 + x_2^2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}{x_1} = {x_2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {ktm} \right)\\{x_1} =  - {x_2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 3 \right)\\1 + x_1^2 + x_2^2 = 0\,\,\,\,\,\left( 4 \right)\end{array} \right.\end{array}$

+) TH1: Kết hợp (3) với (*) ta có: $\left\{ \begin{array}{l}{x_1} =  - {x_2}\\{x_1} + {x_2} = m - 1\end{array} \right. \Leftrightarrow m = 1$.

+) TH2: Từ (4) ta có $x_1^2 + x_2^2 + 1 = 0$ (vô lí vì $x_1^2 \ge 0;\,\,x_2^2 \ge 0 \Rightarrow x_1^2 + x_2^2 + 1 > 0$)

Kết luận: Vậy m = 1 thì tam giác OAB cân tại O.

Với m = 1 thì (d) trở thành: y = 2 là 1 đường thẳng song song với trục hoành và cắt trục tung tại điểm có tung độ bằng 2.

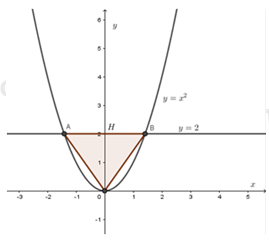
Với m = 1 ta có: Phương trình (1) trở thành:

Ta có: $AB = \sqrt {{{\left( {\sqrt 2  + \sqrt 2 } \right)}^2} + {{\left( {2 - 2} \right)}^2}}  = \sqrt 8$

Ta có: ${S_{OAB}} = \dfrac{1}{2}OH.AB = \dfrac{1}{2}.2.\sqrt 8  = \sqrt 8 \left( {dvdt} \right)$

Câu 5.

Cho nửa đường tròn tâm O đường kính AB, M là một điểm bất kỳ thuộc nửa đường tròn (M khác A, B). Tiếp tuyến tại M cắt các tiếp tuyến Ax và By của nửa đường tròn đó lần lượt tại C và D.

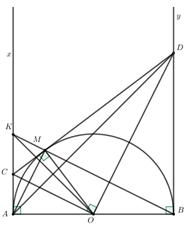
a) Chứng minh $\widehat {COD} = {90^0}$.

Ta có: OC là tia phân giác của góc AOM; OD là tia phân giác của góc BOM (tính chất hai tiếp tuyến cắt nhau)

Mà $\widehat {AOM}$ và $\widehat {BOM}$ là hai góc kề bù $\Rightarrow OC \bot OD$.

$\Rightarrow \widehat {COD} = {90^0}$.

b) Gọi K là giao điểm của BM và Ax. Chứng minh $\Delta KMO \sim \Delta AMD$

Xét tứ giác OBDM có $\angle OBD + \angle OMD = {90^0} + {90^0} = {180^0}$

$\Rightarrow$ Tứ giác OBDM là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 180⁰)

$\Rightarrow \angle ABM = \angle ODM$ (hai góc nội tiếp cùng chắn cung OM)

Lại có $\angle KAM = \angle ABM$ (hai góc nội tiếp cùng chắn cung AM).

$\Rightarrow \angle KAM = \angle ODM$

Xét tam giác AMK và tam giác DMO có:

$\angle KAM = \angle ODM$(cmt)

$\Rightarrow \angle AMK = \angle OMD = {90^0}$

$\Rightarrow \Delta AMK \sim \Delta DMO\,\,\left( {g.g} \right)$

$\Rightarrow \dfrac{{MK}}{{MO}} = \dfrac{{MA}}{{MD}}$

Ta có:

$\begin{array}{l}\angle KMO = \angle KMC + \angle CMO = \angle KMC + {90^0}\\\angle AMD = \angle AMB + \angle BMD = \angle BMD + {90^0}\end{array}$

Mà $\angle KMC = \angle BMD$  (2 góc đối đỉnh)

Nên $\angle KMO = \angle AMD$

Xét tam giác KMO và tam giác AMD có:

$\begin{array}{l}\angle KMO = \angle AMD\,\,\left( {cmt} \right);\\\dfrac{{MK}}{{MO}} = \dfrac{{MA}}{{MD}}\,\,\left( {cmt} \right)\end{array}$

$\Rightarrow \Delta KMO \sim \Delta AMD\,\,\left( {c.g.c} \right)$

c) Tìm giá trị nhỏ nhất của tổng diện tích hai tam giác ACM và BDM.

Ta dễ dàng chứng minh được $\Delta ACM \sim \Delta BOM\,\,\left( {g.g} \right)$

$\Rightarrow \dfrac{{{S_{ACM}}}}{{{S_{OBM}}}} = \dfrac{{A{C^2}}}{{{R^2}}} = \dfrac{{A{M^2}}}{{B{M^2}}}$

Lại có ${S_{OBM}} = \dfrac{1}{2}{S_{MAB}}$

$\Rightarrow {S_{ACM}} = \dfrac{1}{2}{S_{MAB}}.\dfrac{{M{A^2}}}{{M{B^2}}}$ 

Tương tự $\Delta BDM \sim \Delta AOM\,\,\left( {g.g} \right)$

$\Rightarrow \dfrac{{{S_{BDM}}}}{{{S_{AOM}}}} = \dfrac{{B{D^2}}}{{{R^2}}} = \dfrac{{B{M^2}}}{{A{M^2}}}$

Lại có ${S_{AOM}} = \dfrac{1}{2}{S_{MAB}}$

$\Rightarrow {S_{BDM}} = \dfrac{1}{2}{S_{MAB}}.\dfrac{{B{M^2}}}{{A{M^2}}}$

$\Rightarrow {S_{ACM}} + {S_{BDM}} = \dfrac{1}{2}{S_{MAB}}\dfrac{{A{C^2} + B{D^2}}}{{{R^2}}}$

$\Delta MAB \sim \Delta MCD\,\,\left( {g.g} \right)$

$\Rightarrow \dfrac{{{S_{MAB}}}}{{{S_{MCD}}}} = \dfrac{{A{B^2}}}{{C{D^2}}}$

$\Rightarrow {S_{MAB}} = {S_{MCD}}.\dfrac{{4{R^2}}}{{C{D^2}}} = \dfrac{1}{2}R.CD.\dfrac{{4{R^2}}}{{C{D^2}}} = \dfrac{{2{R^3}}}{{CD}}$

$\Rightarrow {S_{ACM}} + {S_{BDM}} = \dfrac{1}{2}.\dfrac{{2{R^3}}}{{CD}}.\dfrac{{A{C^2} + B{D^2}}}{{{R^2}}} = R.\dfrac{{A{C^2} + B{D^2}}}{{CD}}$

Ta có $AC = CM;\,\,BD = BM;\,\,CD = CM + DM$

$\Rightarrow {S_{ACM}} + {S_{BDM}} = R.\dfrac{{C{M^2} + D{M^2}}}{{CM + DM}}$

Áp dụng BĐT Bunhiacopxki ta có ${\left( {CM + DM} \right)^2} \le 2\left( {C{M^2} + D{M^2}} \right) \Rightarrow \dfrac{{C{M^2} + D{M^2}}}{{{{\left( {CM + DM} \right)}^2}}} \ge \dfrac{1}{2}$

$\begin{array}{l} \Rightarrow \dfrac{{C{M^2} + D{M^2}}}{{CM + DM}} \ge \dfrac{1}{2}\left( {CM + DM} \right) = \dfrac{1}{2}CD \ge \dfrac{1}{2}AB = R\\ \Rightarrow {S_{ACM}} + {S_{BDM}} = R.\dfrac{{C{M^2} + D{M^2}}}{{CM + DM}} \ge {R^2}\end{array}$

Dấu bằng xảy ra $\Leftrightarrow \left\{ \begin{array}{l}CM = DM\\CD = AB\end{array} \right.$ , khi đó M là điểm chính giữa của cung AB.

Vậy ${\left( {{S_{ACM}} + {S_{BDM}}} \right)_{\min }} = {R^2} \Leftrightarrow M$ là điểm chính giữa của cung AB.

Câu 6.

a) Cho hàm số $y = f\left( x \right)$  với $f\left( x \right)$ là một biểu thức đại số xác định với mọi số thực $x \ne 0$ . Biết rằng: $f\left( x \right) + 3f\left( {\dfrac{1}{x}} \right) = {x^2}\left( {\forall x \ne 0} \right).$ Tính $f\left( 2 \right)$

Ta có:

$\begin{array}{l}f\left( x \right) + 3f\left( {\dfrac{1}{x}} \right) = {x^2}\left( {\forall x \ne 0} \right).\\ \Rightarrow \left\{ \begin{array}{l}f\left( 2 \right) + 3f\left( {\dfrac{1}{2}} \right) = {2^2} = 4\\f\left( {\dfrac{1}{2}} \right) + 3f\left( 2 \right) = {\left( {\dfrac{1}{2}} \right)^2} = \dfrac{1}{4}\end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l}f\left( 2 \right) + 3f\left( {\dfrac{1}{2}} \right) = 4\\3f\left( {\dfrac{1}{2}} \right) + 9f\left( 2 \right) = \dfrac{3}{4}\end{array} \right.\\ \Rightarrow 8f\left( 2 \right) =  - \dfrac{{13}}{4} \Rightarrow f\left( 2 \right) =  - \dfrac{{13}}{{32}}\end{array}$

b) Cho ba số nguyên dương $a,b,c$ đôi một khác nhau và thỏa mãn: $a$ là ước của $b + c + bc$, $b$  là ước của $c + a + ca$  và $c$ là ước của $a + b + ab$ . Chứng minh $a,b,c$ không đồng thời là các số nguyên tố.

Loigiaihay.com