Đề số 19 - Đề thi vào lớp 10 môn Toán
Đề thi vào lớp 10 môn Toán - Đề số 19 có đáp án và lời giải chi tiết
Đề bài
Bài I (2,0 điểm) Cho hai biểu thức \(A = \dfrac{{\sqrt x + 4}}{{\sqrt x - 1}}\) và \(B = \dfrac{{3\sqrt x + 1}}{{x + 2\sqrt x - 3}} - \dfrac{2}{{\sqrt x + 3}}\) với \(x \ge 0,x \ne 1\)
1) Tính giá trị của biểu thức A khi \(x = 9\)
2) Chứng minh \(B = \dfrac{1}{{\sqrt x - 1}}\)
3) Tìm tất cả các giá trị của x để \(\dfrac{A}{B} \ge \dfrac{x}{4} + 5\)
Bài II. (2,0 điểm) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:
Một mảnh đất hình chữ nhật có chu vi bằng 28 mét và độ dài đường chéo bằng 10 mét. Tính chiều dài và chiều rộng của mảnh đất đó theo đơn vị mét.
Bài III (2,0 điểm)
1) Giải hệ phương trình \(\left\{ \begin{array}{l}4x - \left| {y + 2} \right| = 3\\x + 2\left| {y + 2} \right| = 3\end{array} \right.\)
2) Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d): \(y = \left( {m + 2} \right)x + 3\) và Parabol \(\left( P \right)\,:\,y = {x^2}\)
a) Chứng minh (d) luôn cắt (P) tại hai điểm phân biệt.
b) Tìm tất cả các giá trị của m để (d) cắt (P) tại hai điểm phân biệt có các hoành độ là các số nguyên.
Bài IV. (3,5 điểm)
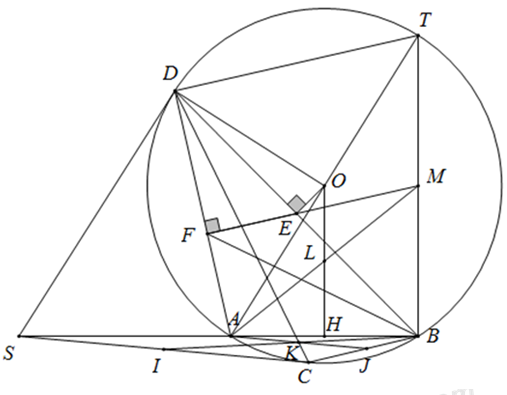
Cho đường tròn (O;R) với dây cung AB không đi qua tâm. Lấy S là một điểm bất kì trên tia đối của tia AB (S khác A). Từ điểm S vẽ hai tiếp tuyến SC, SD với đường tròn (O;R) sao cho điểm C nằm trên cung nhỏ AB (C, D là các tiếp điểm). Gọi H là trung điểm của đoạn thẳng AB.
1) Chứng minh năm điểm C, D, H, O, S thuộc đường tròn đường kính SO.
2) Khi SO = 2R, hãy tính độ dài đoạn thẳng SD theo R và tính số đo \(\widehat {CSD}\) .
3) Đường thẳng đi qua điểm A và song song với đường thẳng SC, cắt đoạn thẳng CD tại điểm K. Chứng minh tứ giác ADHK là tứ giác nội tiếp và đường thẳng BK đi qua trung điểm của đoạn thẳng SC.
4) Gọi E là trung điểm của đoạn thẳng BD và F là hình chiếu vuông góc của điểm E trên đường thẳng AD. Chứng minh rằng, khi điểm S thay đổi trên tia đối của tia AB thì điểm F luôn thuộc một đường tròn cố định.
Bài V (0,5 điểm) Tìm giá trị nhỏ nhất của biểu thức \(P = \sqrt {1 - x} + \sqrt {1 + x} + 2\sqrt x \)
Lời giải chi tiết
Bài I.
Cho hai biểu thức \(A = \dfrac{{\sqrt x + 4}}{{\sqrt x - 1}}\) và \(B = \dfrac{{3\sqrt x + 1}}{{x + 2\sqrt x - 3}} - \dfrac{2}{{\sqrt x + 3}}\) với \(x \ge 0;\,\,x \ne 1\)
1) Tính giá trị của biểu thức A khi \(x = 9\).
Do \(x = 9\) thỏa mãn điều kiện nên thay \(x = 9\) vào biểu thức A ta có:
\(A = \dfrac{{\sqrt 9 + 4}}{{\sqrt 9 - 1}} = \dfrac{{3 + 4}}{{3 - 1}} = \dfrac{7}{2}\)
Vậy khi \(x = 9\) thì \(A = \dfrac{7}{2}\).
2) Chứng minh \(B = \dfrac{1}{{\sqrt x - 1}}\).
Với \(x \ge 0;\,\,x \ne 1\) ta có:
\(\begin{array}{l}B = \dfrac{{3\sqrt x + 1}}{{x + 2\sqrt x - 3}} - \dfrac{2}{{\sqrt x + 3}}\\B = \dfrac{{3\sqrt x + 1}}{{x - \sqrt x + 3\sqrt x - 3}} - \dfrac{2}{{\sqrt x + 3}}\\B = \dfrac{{3\sqrt x + 1}}{{\sqrt x \left( {\sqrt x - 1} \right) + 3\left( {\sqrt x - 1} \right)}} - \dfrac{2}{{\sqrt x + 3}}\\B = \dfrac{{3\sqrt x + 1}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 3} \right)}} - \dfrac{2}{{\sqrt x + 3}}\\B = \dfrac{{3\sqrt x + 1 - 2\left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 3} \right)}}\\B = \dfrac{{3\sqrt x + 1 - 2\sqrt x + 2}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 3} \right)}}\\B = \dfrac{{\sqrt x + 3}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 3} \right)}}\\B = \dfrac{1}{{\sqrt x - 1}}\end{array}\)
Vậy \(B = \dfrac{1}{{\sqrt x - 1}}\,\,,\left( {x \ge 0;x \ne 1} \right)\)
3) Tìm tất cả các giá trị của x để \(\dfrac{A}{B} \ge \dfrac{x}{4} + 5\)
Với \(x \ge 0;\,\,x \ne 1\)
\(\begin{array}{l}\dfrac{A}{B} = \dfrac{{\sqrt x + 4}}{{\sqrt x - 1}}:\dfrac{1}{{\sqrt x - 1}} \\\;\;\;\;\;= \dfrac{{\sqrt x + 4}}{{\sqrt x - 1}}.\left( {\sqrt x - 1} \right) = \sqrt x + 4\\\dfrac{A}{B} \ge \dfrac{x}{4} + 5 \Leftrightarrow \sqrt x + 4 \ge \dfrac{x}{4} + 5\\ \Leftrightarrow 4\sqrt x + 16 \ge x + 20\\ \Leftrightarrow x - 4\sqrt x + 4 \le 0\\ \Leftrightarrow {\left( {\sqrt x - 2} \right)^2} \le 0\\ \Leftrightarrow \sqrt x - 2 = 0\\ \Leftrightarrow x = 4\left( {tm} \right)\end{array}\)
Vậy \(x = 4\) thỏa mãn yêu cầu bài toán.
Bài II:
Nửa chu vi của mảnh đất hình chữ nhật là \(28:2 = 14\;\left( m \right).\)
Gọi chiều dài của mảnh đất là \(x\;\left( m \right),\;\;\left( {\dfrac{{14}}{2} = 7 < x < 14} \right).\)
Khi đó chiều rộng của mảnh đất là: \(14 - x\;\;\left( m \right).\)
Độ dài đường chéo của mảnh đất hình chữ nhật là \(10m\) nên ta có phương trình:
\(\begin{array}{l}\;\;\;\;{x^2} + {\left( {14 - x} \right)^2} = {10^2}\\ \Leftrightarrow 2{x^2} - 28x + 196 - 100 = 0\\ \Leftrightarrow {x^2} - 14x + 48 = 0\\ \Leftrightarrow \left( {x - 6} \right)\left( {x - 8} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 6 = 0\\x - 8 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 6\;\;\;\left( {ktm} \right)\\x = 8\;\;\;\left( {tm} \right)\end{array} \right..\end{array}\)
Với \(x = 8\) thì chiều rộng của mảnh đất là: \(14 - 8 = 6\;m.\)
Vậy chiều dài của mảnh đất là \(8m,\) chiều rộng của mảnh đất là \(6m.\)
Bài III
1) Giải hệ phương trình:
\(\begin{array}{l}\left\{ \begin{array}{l}4x - \left| {y + 2} \right| = 3\\x + 2\left| {y + 2} \right| = 3\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}8x - 2\left| {y + 2} \right| = 6\\x + 2\left| {y + 2} \right| = 3\end{array} \right. \\ \Leftrightarrow \left\{ \begin{array}{l}9x = 9\\x + 2\left| {y + 2} \right| = 3\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 1\\\left| {y + 2} \right| = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\\left[ \begin{array}{l}y + 2 = 1\\y + 2 = - 1\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x = 1\\y = - 1\end{array} \right.\\\left\{ \begin{array}{l}x = 1\\y = - 3\end{array} \right.\end{array} \right.\end{array}\)
Vậy hệ có nghiệm \(\left( {x;y} \right) \in \left\{ {\left( {1; - 1} \right),\left( {1; - 3} \right)} \right\}\).
2)
a) Xét phương trình hoành độ giao điểm: \({x^2} = \left( {m + 2} \right)x + 3\)
\(\Leftrightarrow {x^2} - \left( {m + 2} \right)x - 3 = 0\,\,\,\,\,\left( 1 \right)\)
Số giao điểm của (d) và (P) cũng chính là số nghiệm của phương trình (1)
Ta có:
\(\Delta = {\left( {m + 2} \right)^2} - 4.1.\left( { - 3} \right) \)\(\,= {m^2} + 4m + 16 \)\(\,= {\left( {m + 2} \right)^2} + 12 > 0,\forall m\)
Do đó phương trình \(\left( 1 \right)\) luôn có hai nghiệm phân biệt.
Vậy \(\left( d \right)\) và \(\left( P \right)\) luôn cắt nhau tại hai điểm phân biệt.
b) Với mọi m, (d) luôn cắt (P) tại hai điểm phân biệt có hoành độ \({x_1},{x_2}\)
Theo hệ thức Vi-et, ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = m + 2\\{x_1}{x_2} = - 3\end{array} \right.\)
+) Cách 1:
Do \({x_1}.{x_2} = - 3\) mà \({x_1},{x_2} \in Z\) nên ta có bảng sau:
|
\({x_1}\) |
1 |
-1 |
3 |
-3 |
|
\({x_2}\) |
-3 |
3 |
-1 |
1 |
TH1: \({x_1} = 1;{x_2} = - 3 \Leftrightarrow {x_1} + {x_2} = m + 2 \)
\(\Leftrightarrow 1 - 3 = m + 2 \Leftrightarrow m = - 4\)
TH2: \({x_1} = - 1;{x_2} = 3 \Leftrightarrow {x_1} + {x_2} = m + 2 \)
\(\Leftrightarrow - 1 + 3 = m + 2 \Leftrightarrow m = 0\)
TH3: \({x_1} = 3;{x_2} = - 1 \Leftrightarrow {x_1} + {x_2} = m + 2\)
\(\Leftrightarrow 3 - 1 = m + 2 \Leftrightarrow m = 0\)
TH4: \({x_1} = - 3;{x_2} = 1 \Leftrightarrow {x_1} + {x_2} = m + 2\)
\(\Leftrightarrow - 3 + 1 = m + 2 \Leftrightarrow m = - 4\)
Vậy m = -4 ; m = 0 thỏa mãn yêu cầu bài toán.
+) Cách 2: nên do \({x_1},{x_2} \in Z\) thì \(m \in Z\).
Do \(x{ _1} + {x_2} = m + 2\)
\({x^2} - \left( {m + 2} \right)x - 3 = 0\,\,\)
Xét TH \(x = 0\,\,pt(1) \Leftrightarrow - 3 = 0\left( {ktm} \right) \Rightarrow x \ne 0\)
Ta có: \({x^2} - \left( {m + 2} \right)x - 3 = 0 \)
\(\Leftrightarrow m + 2 = \dfrac{{{x^2} - 3}}{x} \Leftrightarrow m = x - 2 - \dfrac{3}{x}\)
Do \(x \in Z\) nên \(m \in Z \Leftrightarrow x \in U\left( 3 \right) = \left\{ { \pm 1; \pm 3} \right\}\)
Ta có bảng:
|
x |
-1 |
1 |
-3 |
3 |
|
m |
0 |
-4 |
-4 |
0 |
\({x^2} = \left( {m + 2} \right)x + 3\)
\(\Leftrightarrow {x^2} - \left( {m + 2} \right)x - 3 = 0\,\,\,\,\,\left( 1 \right)\)
+) Với \(m = 0\) ta có (1) trở thành: \({x^2} - 2x - 3 = 0\)
Có: \(a - b + c = 1 + 2 - 3 = 0\) nên phương trình có 2 nghiệm phân biệt: \({x_1} = - 1;{x_2} = 3\)
Vậy m = 0 thỏa mãn
+) Với \(m = - 4\) ta có (1) trở thành: \({x^2} + 2x - 3 = 0\)
Có: \(a + b + c = 1 + 2 - 3 = 0\) nên phương trình có 2 nghiệm phân biệt: \({x_1} = 1;{x_2} = - 3\)
Vậy m = - 4 thỏa mãn
Vậy \(m \in \left\{ { - 4;0} \right\}\) thỏa mãn yêu cầu bài toán.
Bài IV.
1) Xét \(\left( O \right)\) có \(SC,\,\;\;SD\) là hai tiếp tuyến nên \(\angle SCO = \angle SDO = {90^0}.\)
Ta có: H là trung điểm của AB nên \(OH \bot AB\) (quan hệ vuông góc giữa đường kính và dây cung)
Ta có: \(\angle SDO = \angle SCO = \angle SHO = {90^0}\left( {gt} \right)\)
Suy ra: ba điểm \(\,D,\;H,C\) cùng nhìn SO dưới một góc \({90^0}\)
Do đó \(\,D,\;H,C\)thuộc đường tròn đường kính \(SO.\)
Vậy năm điểm\(\,D,\;H,C,S,O\) cùng thuộc đường tròn đường kính SO(đpcm)
2) Với \(SO = 2R\).
Xét tam giác \(SDO\) vuông tại \(D\), theo định lý Pitago ta có
\(S{D^2} = S{O^2} - O{D^2} = {\left( {2R} \right)^2} - {R^2} = 3{R^2}\) \( \Rightarrow SD = \sqrt 3 R\) .
Xét tam giác \(SDO\) vuông tại \(D\) ta có \(\cos \angle DSO = \dfrac{{SD}}{{SO}} = \dfrac{{\sqrt 3 R}}{{2R}} = \dfrac{{\sqrt 3 }}{2}\) (tỉ số lượng giác của góc nhọn)
\( \Rightarrow \angle DSO = {30^0}.\)
Xét \(\left( O \right)\) có \(SD,\,SC\) là hai tiếp tuyến cắt nhau tại \(S\) nên \(SO\) là phân giác \(\angle DSC\) (tính chất hai tiếp tuyến cắt nhau)
Suy ra \(\angle DSC = 2\angle DSO = {2.30^0} = {60^0}.\)
Vậy khi \(SO = 2R\) thì \(SD = R\sqrt 3 \) và \(\angle CSD = {60^0}.\)
3) * Vì 5 điểm \(S,D,O,H,C\) cùng thuộc một đường tròn (câu 1) nên \(\angle HSC = \angle HDC\) (3) (hai góc nội tiếp cùng chắn cung HC)
Lại có \(AK//SC \Rightarrow \angle HAK = \angle HSC\) (hai góc ở vị trí đồng vị) (4)
Từ (3) và (4) suy ra \(\angle KAH = \angle KDH\left( { = \angle HSC} \right)\)
Xét tứ giác \(AKHD\) có \(\angle KAH = \angle KDH\) nên tứ giác \(AKHD\) là tứ giác nội tiếp (hai đỉnh kề nhau cùng nhìn cạnh đối diện dưới các góc bằng nhau).
* Kéo dài \(AK\) cắt \(BC\) tại \(J\), kéo dài \(BK\) cắt \(SC\) tại \(I\).
Vì \(AK//SI \Rightarrow \dfrac{{AK}}{{SI}} = \dfrac{{BK}}{{BI}}.\,\,\left( {Ta - let} \right)\)
\(\begin{array}{l}KJ//CI \Rightarrow \dfrac{{KJ}}{{CI}} = \dfrac{{BK}}{{BI}}\left( {Ta\, - let} \right).\\ \Rightarrow \dfrac{{AK}}{{SI}} = \dfrac{{KJ}}{{CI}}\left( { = \dfrac{{BK}}{{BI}}} \right)\;\;\left( * \right)\end{array}\)
Xét đường tròn tâm \(\left( O \right)\) có \(\angle ABC = \angle ADC\) (hai góc nội tiếp cùng chắn cung \(AC\) ) (5)
Mà tứ giác \(ADHK\) nội tiếp (cmt) nên ta có \(\angle ADK = \angle AHK\) (6)
Từ (5) và (6) suy ra \(\angle AHK = \angle ABC\;\;\left( {\angle ADK} \right)\) mà hai góc ở vị trí đồng vị nên \(KH//JB\)
Mà \(H\) là trung điểm \(AB\) nên \(K\) là trung điểm \(AJ\) (tính chất của đường trung bình)
suy ra \(AK = KJ\) . (**)
Từ (*) và (**) suy ra \(SI = CI\) hay \(I\) là trung điểm \(SC\).
Suy ra \(BK\) đi qua trung điểm của \(SC\). (đpcm)
4) Gọi AT là đường kính của (O), M là trung điểm BT
Ta có góc \(\angle ADT = 90^\circ \)(góc nội tiếp chắn nửa đường tròn)
⇒ AD ⊥ DT
Mà EF ⊥ AD (gt) nên EF // DT
Ta có EM // DT (đường trung bình)
⇒ E, F, M thẳng hàng (theo tiên đề Ơclit về đường thẳng song song)
Ta có \(\angle ABM = 90^\circ \)(góc nội tiếp chắn nửa đường tròn)
⇒ \(\angle ABM + \angle AFM = 90^\circ + 90^\circ = 180^\circ \)
⇒ Tứ giác AFMB nội tiếp đường tròn đường kính AM.
Gọi L là trung điểm AM ⇒ L là tâm đường tròn ngoại tiếp ∆ ABM
⇒ Đường tròn tâm L, bán kính LA ngoại tiếp tứ giác AFMB
Ta chứng minh L là điểm cố định:
Ta có OL // TM (đường trung bình), OH // TB (đường trung bình)
⇒ O, L, H thẳng hàng (Tiên đề Ơclit về đường thẳng song song)
Mặt khác ta có \(OL = \dfrac{1}{2}TM;\) \(OH = \dfrac{1}{2}TB;\) \(TM = \dfrac{1}{2}TB\)
\(\Rightarrow OH = TM \Rightarrow OL = \dfrac{1}{2}OH\)
⇒ L là trung điểm OH. Mà AB cố định \( \Rightarrow H\) cố định \( \Rightarrow OH\) cố định ⇒ L cố định
Vậy khi S thay đổi trên tia đối của AB thì F luôn nằm trên đường tròn tâm L, bán kính LA, với L là trung điểm OH.
Bài V:
Điều kiện: \(\left\{ \begin{array}{l}1 - x \ge 0\\1 + x \ge 0\\x \ge 0\end{array} \right. \Leftrightarrow 0 \le x \le 1.\)
Với \(0 \le x \le 1,\) ta có: \(x\left( {1 - x} \right) \ge 0 \)
\(\Leftrightarrow \sqrt {x\left( {1 - x} \right)} \ge 0\)
\(\Leftrightarrow 2\sqrt {x\left( {1 - x} \right)} \ge 0\)
\(\begin{array}{l} \Leftrightarrow x + 2\sqrt {x\left( {1 - x} \right)} + 1 - x \ge 1\\ \Leftrightarrow {\left( {\sqrt x + \sqrt {1 - x} } \right)^2} \ge 1\\ \Leftrightarrow \sqrt x + \sqrt {1 - x} \ge 1.\\ \Rightarrow P = \sqrt {1 - x} + \sqrt {1 + x} + 2\sqrt x \\\;\;\;\;= \sqrt x + \sqrt {1 - x} + \sqrt {1 + x} + \sqrt x \\\;\;\;\ge 1 + \sqrt {1 + x} + \sqrt x .\end{array}\)
Với \(x \ge 0 \Rightarrow \sqrt x + \sqrt {x + 1} \ge 1 \)
\(\Rightarrow P \ge 1 + \sqrt x + \sqrt {x + 1} \ge 2.\)
Dấu “=” xảy ra \( \Leftrightarrow x = 0.\)
Vậy \(Min\;P = 2\;\;khi\;\;x = 0.\)
Loigiaihay.com













Danh sách bình luận