Đề số 10 - Đề thi vào lớp 10 môn Toán

Đề bài

Câu 1 (4 điểm) Tính giá trị của các biểu thức sau:

$\begin{array}{l}a)\;A = \sqrt {16 + 9}  - 2\\b)\;B = \sqrt {{{\left( {\sqrt 3  - 1} \right)}^2}}  + 1\end{array}$  

Câu 2 (1,5 điểm)

Cho biểu thức $P = \left( {\frac{{x - 6}}{{x + 3\sqrt x }} - \frac{1}{{\sqrt x }} + \frac{1}{{\sqrt x  + 3}}} \right):\frac{{2\sqrt x  - 6}}{{x + 1}}$ với $x > 0,\;\;x \ne 9.$

a) Rút gọn biểu thức P.

b) Tìm giá trị của x để $P = 1.$

Câu 3 (2,5 điểm)

1) Cho đường thẳng $\left( d \right):\;\;y =  - \dfrac{1}{2}x + 2.$

a) Tìm $m$ để đường thẳng $\left( \Delta  \right):\;y = \left( {m - 1} \right)x + 1$ song song với đường thẳng $\left( d \right).$

b) Gọi $A,\;B$ là giao điểm của $\left( d \right)$ với parabol $\left( P \right):\;\;y = \dfrac{1}{4}{x^2}.$ Tìm tọa độ điểm $N$ nằm trên trục hoành sao cho $NA + NB$ nhỏ nhất.

2) Cho hệ phương trình: $\left\{ \begin{array}{l}x + ay = 3a\\ - ax + y = 2 - {a^2}\end{array} \right.\;\;\;\left( I \right)$ với $a$ là tham số.

a) Giải hệ phương trình (I) khi $a = 1.$

b) Tìm $a$ để hệ phương trình (I) có nghiệm duy nhất $\left( {x;\;y} \right)$ thỏa mãn $\dfrac{{2y}}{{{x^2} + 3}}$ là số nguyên.

Câu 4 (2 điểm)

Cho phương trình: ${x^2} - 2x + m - 3 = 0\;\;\;\left( 1 \right)$  với $m$ là tham số,

a) Giải phương trình $\left( 1 \right)$ khi $m = 0.$

b) Tìm tất cả các giá trị của $m$ để phương trình $\left( 1 \right)$ có hai nghiệm phân biệt ${x_1},\;\;{x_2}$ thỏa mãn:

$x_1^2 + 12 = 2{x_2} - {x_1}{x_2}.$

Câu 5 (3,0 điểm)

Cho đường tròn (O) đường kính AB = 2R, C là trung điểm OA và dây cung MN vuông góc với OA tại C. Gọi K là điểm tùy ý trên cung nhỏ BM (K khác B, M), H là giao điểm của AK và MN.

a) Chứng minh tứ giác BCHK là tứ giác nội tiếp.

b) Chứng minh $AH.AK = A{M^2}$

c) Xác định vị trí của điểm K để $KM + KN + KB$ đạt giá trị lớn nhất và giá trị nhỏ nhất.

Lời giải chi tiết

Câu 1:

$\begin{array}{l}a)\;A = \;\sqrt {16 + 9}  - 2 = \sqrt {25}  - 2 \\\;\;\;\;\;\;\;\;= \sqrt {{5^2}}  - 2 = 5 - 2 = 3.\\b)\;B = \sqrt {{{\left( {\sqrt 3  - 1} \right)}^2}}  + 1 \\\;\;\;\;\;\;\;\;= \left| {\sqrt 3  - 1} \right| + 1 = \sqrt 3  - 1 + 1 \\\;\;\;\;\;\;\;\;= \sqrt 3 \;\;\left( {do\;\;\sqrt 3  - 1 > 0} \right).\end{array}$

Câu 2:

Cho biểu thức $P = \left( {\dfrac{{x - 6}}{{x + 3\sqrt x }} - \dfrac{1}{{\sqrt x }} + \dfrac{1}{{\sqrt x  + 3}}} \right):\dfrac{{2\sqrt x  - 6}}{{x + 1}}$ với $x > 0,\;\;x \ne 9.$

a) Rút gọn biểu thức P.

Điều kiện: $x > 0,\;x \ne 9.$

$\begin{array}{l}P = \left( {\dfrac{{x - 6}}{{x + 3\sqrt x }} - \dfrac{1}{{\sqrt x }} + \dfrac{1}{{\sqrt x  + 3}}} \right):\dfrac{{2\sqrt x  - 6}}{{x + 1}}\\\;\;\; = \left( {\dfrac{{x - 6}}{{\sqrt x \left( {\sqrt x  + 3} \right)}} - \dfrac{1}{{\sqrt x }} + \dfrac{1}{{\sqrt x  + 3}}} \right):\dfrac{{2\left( {\sqrt x  - 3} \right)}}{{x + 1}}\\\;\;\; = \dfrac{{x - 6 - \left( {\sqrt x  + 3} \right) + \sqrt x }}{{\sqrt x \left( {\sqrt x  + 3} \right)}}.\dfrac{{x + 1}}{{2\left( {\sqrt x  - 3} \right)}}\\\;\;\; = \dfrac{{x - 6 - \sqrt x  - 3 + \sqrt x }}{{\sqrt x \left( {\sqrt x  + 3} \right)}}.\dfrac{{x + 1}}{{2\left( {\sqrt x  - 3} \right)}}\\\;\;\; = \dfrac{{\left( {x - 9} \right)\left( {x + 1} \right)}}{{2\sqrt x \left( {x - 9} \right)}} = \dfrac{{x + 1}}{{2\sqrt x }}.\end{array}$

b) Tìm giá trị của x để $P = 1.$

Điều kiện: $x > 0,\;x \ne 9.$

$\begin{array}{l}P = 1 \Leftrightarrow \dfrac{{x + 1}}{{2\sqrt x }} = 1\\ \Leftrightarrow x + 1 = 2\sqrt x  \Leftrightarrow x - 2\sqrt x  + 1 = 0\\ \Leftrightarrow {\left( {\sqrt x  - 1} \right)^2} = 0 \Leftrightarrow \sqrt x  - 1 = 0 \\\Leftrightarrow \sqrt x  = 1 \Leftrightarrow x = 1\;\;\left( {tm} \right).\end{array}$

Vậy $x = 1$ thì $P = 1.$

Câu 3:

1) Cho đường thẳng $\left( d \right):\;\;y =  - \dfrac{1}{2}x + 2.$

a) Tìm $m$ để đường thẳng $\left( \Delta  \right):\;y = \left( {m - 1} \right)x + 1$ song song với đường thẳng $\left( d \right).$

b) Gọi $A,\;B$ là giao điểm của $\left( d \right)$ với parabol $\left( P \right):\;\;y = \dfrac{1}{4}{x^2}.$ Tìm tọa độ điểm $N$ nằm trên trục hoành sao cho $NA + NB$ nhỏ nhất.

1) Cho đường thẳng $\left( d \right):\;\;y =  - \dfrac{1}{2}x + 2.$

a) Tìm $m$ để đường thẳng $\left( \Delta  \right):\;y = \left( {m - 1} \right)x + 1$ song song với đường thẳng $\left( d \right).$

Đường thẳng $\left( d \right)//\left( \Delta  \right) \Leftrightarrow \left\{ \begin{array}{l}m - 1 =  - \dfrac{1}{2}\\1 \ne 2\end{array} \right. \Leftrightarrow m = \dfrac{1}{2}.$

Vậy $m = \dfrac{1}{2}.$

b) Gọi $A,\;B$ là giao điểm của $\left( d \right)$ với parabol $\left( P \right):\;\;y = \dfrac{1}{4}{x^2}.$ Tìm tọa độ điểm $N$ nằm trên trục hoành sao cho $NA + NB$ nhỏ nhất.

Hoành độ giao điểm của đường thẳng $\left( d \right)$ và $\left( P \right)$ là nghiệm của phương trình:

$\begin{array}{l}\dfrac{1}{4}{x^2} =  - \dfrac{1}{2}x + 2 \Leftrightarrow {x^2} + 2x - 8 = 0\;\;\\ \Leftrightarrow \left( {x - 2} \right)\left( {x + 4} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x - 2 = 0\\x + 4 = 0\end{array} \right. \\\Leftrightarrow \left[ \begin{array}{l}x = 2 \Rightarrow y = 1 \Rightarrow A\left( {2;\;1} \right)\\x =  - 4 \Rightarrow y = 4 \Rightarrow B\left( { - 4;\;4} \right)\end{array} \right..\end{array}$

Khi đó $A\left( {2;\;1} \right),\;\;B\left( { - 4;\;4} \right)$   là hai giao điểm của 2 đồ thị hàm số.

Gọi A’ là điểm đối xứng với A qua Ox thì $A'\left( {2; - 1} \right)$

Khi đó ta có: $NA = NA'$ nên $NA + NB\,\,\min  \Leftrightarrow NA' + NB\,\,\min$

Mà A’, B nằm khác phía với trục Ox

Nên để NA’ + NB min thì A’, B, N thẳng hàng.

Từ đó suy ra điểm N cần tìm là giao điểm của đường thẳng A’B với trục hoành: $N\left( {n;0} \right)$

Gọi phương trình đường thẳng (d’) đi qua hai điểm A’, B là: $y = ax + b$

Do A’, B thuộc đường thẳng (d’) nên ta có hệ phương trình:

$\left\{ \begin{array}{l}2a + b =  - 1\\ - 4a + b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a =  - \dfrac{5}{6}\\b = \dfrac{2}{3}\end{array} \right.$

Ta có phương trình đường thẳng (d’) là: $y =  - \dfrac{5}{6}x + \dfrac{2}{3}$

Khi đó điểm N thuộc đường thẳng d’ và $N\left( {\dfrac{4}{5};0} \right)$

Vậy khi $N\left( {\dfrac{4}{5};0} \right)$ thì ${\left( {NA + NB} \right)_{\min }} = A'B$$\, = \sqrt {{{\left( { - 4 - 2} \right)}^2} + {{\left( {4 + 1} \right)}^2}}  = \sqrt {61}$.

2) Cho hệ phương trình: $\left\{ \begin{array}{l}x + ay = 3a\\ - ax + y = 2 - {a^2}\end{array} \right.\;\;\;\left( I \right)$ với $a$ là tham số.

a) Giải hệ phương trình (I) khi $a = 1.$

Thay $a = 1$ vào hệ phương trình ta được:

$\left( I \right) \Leftrightarrow \left\{ \begin{array}{l}x + y = 3\\ - x + y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2y = 4\\x = 3 - y\end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l}y = 2\\x = 3 - 2 = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 2\end{array} \right..$

Vậy với $a = 1$ thì hệ phương trình có nghiệm duy nhất $\left( {x;y} \right) = \left( {1;\;2} \right).$

b) Tìm $a$ để hệ phương trình (I) có nghiệm duy nhất $\left( {x;\;y} \right)$ thỏa mãn $\dfrac{{2y}}{{{x^2} + 3}}$ là số nguyên.

+) Với $a = 0$ ta có: $\left( I \right) \Leftrightarrow \left\{ \begin{array}{l}x = 0\\y = 2\end{array} \right. \Rightarrow$ hệ phương trình có nghiệm duy nhất.

+) Với $a \ne 0:$ Hệ phương trình có nghiệm duy nhất $\Leftrightarrow \dfrac{1}{{ - a}} \ne \dfrac{a}{1}\;\;\left( {a \ne 0} \right)$

$\Leftrightarrow  - {a^2} \ne 1$ (luôn đúng).

Vậy hệ phương trình luôn có nghiệm duy nhất với mọi $a.$

Ta có: $\left( I \right) \Leftrightarrow \left\{ \begin{array}{l}x = 3a - ay\\ - a\left( {3a - ay} \right) + y = 2 - {a^2}\end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l}x = 3a - ay\\ - 3{a^2} + {a^2}y + y = 2 - {a^2}\end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l}x = 3a - ay\\y\left( {{a^2} + 1} \right) = 2 + 2{a^2}\end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l}x = 3a - ay\\y = \dfrac{{2{a^2} + 2}}{{{a^2} + 1}} = 2\end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l}x = 3a - 2a = a\\y = 2\end{array} \right..$

$\Rightarrow$ Hệ phương trình có nghiệm duy nhất $\left( {x;\;y} \right) = \left( {a;\;2} \right).$

Ta có: $\dfrac{{2y}}{{{x^2} + 3}} = \dfrac{{2.2}}{{{a^2} + 3}} = \dfrac{4}{{{a^2} + 3}}.$

$\dfrac{{2y}}{{{x^2} + 3}} \in Z \Leftrightarrow \dfrac{4}{{{a^2} + 3}} \in Z$

$\Leftrightarrow \left( {{a^2} + 3} \right) \in U\left( 4 \right)$

Mà $U\left( 4 \right) = \left\{ { \pm 1;\; \pm 2;\; \pm 4} \right\}.$

Lại có: ${a^2} + 3 \ge 3\;\;\forall \;a$

$\Rightarrow {a^2} + 3 = 4 \Leftrightarrow {a^2} = 1$

$\Leftrightarrow \left[ \begin{array}{l}a = 1\\a =  - 1\end{array} \right..$

Vậy $a =  \pm 1$ thỏa mãn điều kiện bài toán.

Câu 4:

Cho phương trình: ${x^2} - 2x + m - 3 = 0\;\;\;\left( 1 \right)$  với $m$ là tham số,

a) Giải phương trình $\left( 1 \right)$ khi $m = 0.$

Thay $m = 0$ vào phương trình $\left( 1 \right)$ ta có:

$\left( 1 \right) \Leftrightarrow {x^2} - 2x - 3 = 0$

$\Leftrightarrow \left( {x - 3} \right)\left( {x + 1} \right) = 0$

$\Leftrightarrow \left[ \begin{array}{l}x - 3 = 0\\x + 1 = 0\end{array} \right.$

$\Leftrightarrow \left[ \begin{array}{l}x = 3\\x =  - 1\end{array} \right..$

Vậy với $m = 0$ thì phương trình $\left( 1 \right)$ có hai nghiệm phân biệt $x =  - 1$ và $x = 3.$

b) Tìm tất cả các giá trị của $m$ để phương trình $\left( 1 \right)$ có hai nghiệm phân biệt ${x_1},\;\;{x_2}$ thỏa mãn:

$x_1^2 + 12 = 2{x_2} - {x_1}{x_2}.$

Phương trình $\left( 1 \right)$ có hai nghiệm phân biệt $\Leftrightarrow \Delta ' > 0 \Leftrightarrow 1 - m + 3 > 0 \Leftrightarrow m < 4.$

Áp dụng hệ thức Vi-ét ta có: $\left\{ \begin{array}{l}{x_1} + {x_2} = 2\\{x_1}{x_2} = m - 3\end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l}{x_2} = 2 - {x_1}\;\;\;\;\;\;\left( 1 \right)\\{x_1}{x_2} = m - 3\;\;\;\;\;\left( 2 \right)\end{array} \right.$

Theo đề bài ta có: $x_1^2 + 12 = 2{x_2} - {x_1}{x_2}\;\;\;\left( 3 \right)$

Thế $\left( 1 \right)$ vào $\left( 2 \right)$ ta có:

$\begin{array}{l}\;\;\;\;\;x_1^2 + 12 = 2\left( {2 - {x_1}} \right) - {x_1}\left( {2 - {x_1}} \right)\\ \Leftrightarrow x_1^2 + 12 = 4 - 2{x_1} - 2{x_1} + x_1^2\\ \Leftrightarrow  - 4{x_1} = 8 \Leftrightarrow {x_1} =  - 2\\ \Rightarrow {x_2} = 2 - {x_1} = 4.\\ \Rightarrow {x_1}{x_2} = m - 3\\ \Leftrightarrow m - 3 =  - 8 \Leftrightarrow m =  - 5\;\;\left( {tm} \right).\end{array}$

Vậy $m =  - 5.$

Câu 5.

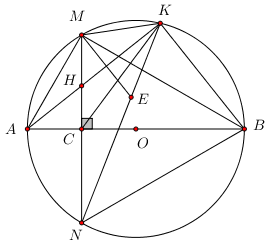
a) Ta có $\widehat {AKB} = {90^0}$ (góc nội tiếp chắn nửa đường tròn).

Xét tứ giác BCHK có $\widehat {BCH} + \widehat {BKH} = {90^0} + {90^0} \Rightarrow$ Tứ giác BCHK là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 180⁰)

b) Ta có $OA \bot MN$ tại C $\Rightarrow C$ là trung điểm của MN (quan hệ vuông góc giữa đường kính và dây cung).

$\Rightarrow \Delta AMN$ có AC là đường cao đồng thời là trung tuyến

$\Rightarrow \Delta AMN$ cân tại $A \Rightarrow AM = AN \Rightarrow$ sđ cung AM = sđ cung AN.

$\Rightarrow \widehat {AMN} = \widehat {AKM}$ (hai góc nội tiếp chắn hai cung bằng nhau)

Xét tam giác AMN và AKM có:

$\widehat {MAK}$ chung;

 $\widehat {AMN} = \widehat {AKM}\,\,\left( {cmt} \right)$;

$\Rightarrow \Delta AMH \sim \Delta AKM\,\,\,\left( {g.g} \right)$

$\Rightarrow \dfrac{{AM}}{{AK}} = \dfrac{{AH}}{{AM}} \Rightarrow A{M^2} = AH.AK$

c) Lấy điểm E thuộc KN sao cho $KM = KE$.

Xét tam giác vuông AMB có: $A{M^2} = AC.AB = \dfrac{R}{2}.2R = {R^2}$

$\Rightarrow AM = R$ (hệ thức lượng trong tam giác vuông)

$\Rightarrow \sin \widehat {ABM} = \dfrac{{AM}}{{AB}} = \dfrac{R}{{2R}} = \dfrac{1}{2}$$\,\Rightarrow \widehat {ABM} = {30^0}$$\Rightarrow \widehat {MBN} = {60^0}$ (tính đối xứng).

$\Rightarrow \widehat {MKE} = \widehat {MKN} = \widehat {MBN} = {60^0}$ (hai góc nội tiếp cùng chắn cung MN).

$\Rightarrow \Delta AKE$ đều $\Rightarrow KM = KE = ME$.

Ta có AB là trung trực của MN $\Rightarrow BM = BN$

Lại có $\widehat {MBN} = {60^0}\,\,\left( {cmt} \right) \Rightarrow \Delta BMN$ đều $\Rightarrow MB = MN = BN$ và $\widehat {BMN} = {60^0}$

$\begin{array}{l} \Rightarrow \widehat {BMN} = \widehat {KME} = {60^0}\\ \Rightarrow \widehat {BMN} - \widehat {BME} = \widehat {KME} - \widehat {BME}\\ \Leftrightarrow \widehat {EMN} = \widehat {KMB}\end{array}$ 

Xét tam giác KMB và tam giác EMN có:

KM = EM;

MB = MN;

$\widehat {EMN} = \widehat {KMB}\,\,\left( {cmt} \right);$

$\Rightarrow \Delta KMB = \Delta EMN\,\,\left( {c.g.c} \right)$

$\Rightarrow KB = EN$ (hai cạnh tương ứng)

$\Rightarrow S = KM + KN + KB$

         $= KE + \left( {KE + EN} \right) + EN$

         $= 2\left( {KE + EN} \right) = 2KN$

KN lớn nhất khi và chỉ khi KN là đường kính của đường tròn O, khi đó KN = 2R và ${S_{\max }} = 4R$

KN nhỏ nhất khi và chỉ khi $K \equiv M \Rightarrow KN = MN \Rightarrow {S_{\min }} = 2MN$

Xét tam giác vuông AMB cos $M{C^2} = AC.BC = \dfrac{R}{2}.\dfrac{{3R}}{2} = \dfrac{{3{R^2}}}{4}$

$\Rightarrow MC = \dfrac{{R\sqrt 3 }}{2} \Rightarrow MN = R\sqrt 3$

$\Rightarrow {S_{\min }} = 2R\sqrt 3$

Vậy ${\left( {KM + KN + KB} \right)_{\max }} = 4R$ và  ${\left( {KM + KN + KB} \right)_{\min }} = 2R\sqrt 3$.

Loigiaihay.com