Bài 3 trang 129 Tài liệu dạy – học Toán 9 tập 1

Giải bài tập Cho đường tròn (O). Bốn điểm A, B, C, D

Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn

Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa - GDCD

Đề bài

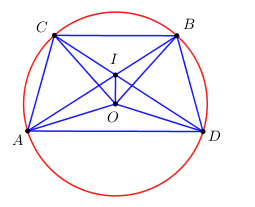
Cho đường tròn (O). Bốn điểm A, B, C, D nằm trên đường tròn theo thứ tự chiều quay kim đồng hồ, sao cho AB = CD, AB và CD cắt nhau tại I.

a) Chứng minh OI là phân giác của góc AID

b) Chứng minh IB = IC ; IA = ID.

Phương pháp giải - Xem chi tiết

+) Chứng minh \(\Delta OAB = \Delta ODC\).

+) Chứng minh \(\Delta IAD\) có \(IA = ID\), từ đó chứng minh \(\Delta IOA = \Delta IOD\).

b) Từ \(AB = CD,\,\,IA = ID \Rightarrow IB = IC\).

Lời giải chi tiết

Xét \(\Delta OAB\) và \(\Delta ODC\) có :

\(\begin{array}{l}OA = OD = R\\OB = OC = R\\AB = CD\,\left( {gt} \right)\\ \Rightarrow \Delta OAB = \Delta ODC\,\,\left( {c.c.c} \right) \\\Rightarrow \widehat {OAB} = \widehat {ODC}\end{array}\)

Xét tam giác OAD cân tại O

\( \Rightarrow \widehat {OAD} = \widehat {ODA}\\ \Rightarrow \widehat {OAD} + \widehat {OAB} = \widehat {ODA} + \widehat {ODC} \\\Rightarrow \widehat {IAD} = \widehat {IDA}\)

\( \Rightarrow \Delta IAD\) cân tại I \( \Rightarrow IA = ID\).

Xét \(\Delta IOA\) và \(\Delta IOD\) có

\(\begin{array}{l}IA = ID\,\,\left( {cmt} \right)\\IO\,\,chung\\OA = OD = R\\ \Rightarrow \Delta IOA = \Delta IOD\,\,\left( {c.c.c} \right) \\\Rightarrow \widehat {OIA} = \widehat {OID}\end{array}\)

Vậy OI là phân giác của \(\widehat {AID}\).

b) Ta có \(AB = CD\,\left( {gt} \right),\,\,IA = ID\,\,\left( {cmt} \right)\\ \Rightarrow AB - IA = CD - ID \Rightarrow IB = IC\).

Loigiaihay.com