-
Chương 1: Số hữu tỉ
-
Chương 2: Số thực
-
Chương 3: Hình học trực quan
-
Chương 4: Góc. Đường thẳng song song
-
Chương 5: Một số yếu tố thống kê và xác suất
-
Chương 6: Biểu thức đại số
-
Chương 7: Tam giác
- Bài 1: Tổng ba góc của một tam giác
- Bài 2: Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác
- Bài 3: Hai tam giác bằng nhau
- Bài 4: Trường hợp bằng nhau thứ nhất của tam giác cạnh - cạnh - cạnh
- Bài 5: Trường hợp bằng nhau thứ hai của tam giác cạnh - góc - cạnh
- Bài 6: Trường hợp bằng nhau thứ ba của tam giác góc - cạnh - góc
- Bài 7: Tam giác cân
- Bài 8: Đường vuông góc và đường xiên
- Bài 9: Đường trung trực của một đoạn thẳng
- Bài 10: Tính chất ba đường trung tuyến của tam giác
- Bài 11: Tính chất ba đường phân giác của tam giác
- Bài 12: Tính chất ba đường trung trực của tam giác
- Bài 13: Tính chất ba đường cao của tam giác
Trắc nghiệm Bài 1: Góc ở vị trí đặc biệt Toán 7 Cánh diều
Đề bài
Hai đường thẳng zz’ và tt’ cắt nhau tại $A$. Góc đối đỉnh với \(\widehat {zAt'}\) là:
-
A.
\(\widehat {z'At'}\)
-
B.
\(\widehat {z'At}\)
-
C.
\(\widehat {zAt'}\) \(\)
-
D.
\(\widehat {zAt}\)
Cho góc \(xBy\) đối đỉnh với góc \(x'By'\) và \(\widehat {xBy} = 60^\circ \) . Tính số đo góc \(x'By'.\)
-
A.
$30^\circ$
-
B.
$120^\circ$
-
C.
$90^\circ$
-
D.
$60^\circ$
Cho hai đường thẳng \(xx'\) và \(yy'\) giao nhau tại \(O\) sao cho \(\widehat {xOy} = 45^\circ \) . Chọn câu sai.
-
A.
$\widehat {x'Oy} = 135^\circ $
-
B.
$\widehat {x'Oy'} = 45^\circ $
-
C.
$\widehat {xOy'} = 135^\circ $
-
D.
$\widehat {x'Oy'} = 135^\circ $
Cho cặp góc đối đỉnh \(\widehat {tOz}\) và \(\widehat {t'Oz'}\) (\(Oz\) và $Oz'$ là hai tia đối nhau). Biết \(\widehat {tOz'} = 4.\widehat {tOz}\). Tính các góc \(\widehat {tOz}\) và \(\widehat {t'Oz'}.\)
-
A.
\(\widehat {zOt} = \widehat {z'Ot'} = 72^\circ \)
-
B.
\(\widehat {zOt} = \widehat {z'Ot'} = 30^\circ \)
-
C.
\(\widehat {zOt} = \widehat {z'Ot'} = 36^\circ \)
-
D.
\(\widehat {zOt} = 72^\circ ;\,\widehat {z'Ot'} = 36^\circ \)
Vẽ góc $xOy$ có số đo bằng $35^\circ$. Vẽ góc $x'Oy'$ đối đỉnh với góc $xOy.$ Viết tên các góc có số đo bằng $145^o.$
-
A.
\(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy'}\)
-
B.
\(\widehat {xOy}\,\,;\,\,\widehat {x'Oy'}\)
-
C.
\(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy}\)
-
D.
\(\widehat {xOy'}\,\,;\,\,\widehat {xOy}\)
Hai đường thẳng \(AB\) và \(CD\) cắt nhau tại $O$ tạo thành \(\widehat {AOC} = 60^\circ \) . Gọi \(OM\) là phân giác \(\widehat {AOC}\) và \(ON\) là tia đối của tia \(OM\). Tính \(\widehat {BON}\) và \(\widehat {DON}.\)
-
A.
\(\widehat {BON} = \widehat {DON} = 25^\circ \)
-
B.
\(\widehat {BON} = \widehat {DON} = 30^\circ \)
-
C.
\(\widehat {BON} = \widehat {DON} = 60^\circ \)
-
D.
\(\widehat {BON} = \widehat {DON} = 45^\circ \)
Hai đường thẳng $AB$ và $CD$ cắt nhau tại $O.$ Biết \(\widehat {AOC} - \widehat {AOD} = {50^0}.\) Chọn câu đúng.
-
A.
\(\widehat {AOC} = 110^\circ \)
-
B.
\(\widehat {BOC} = 65^\circ \)
-
C.
\(\widehat {BOD} = 120^\circ \)
-
D.
\(\widehat {AOD} = 50^\circ \)
Hai đường thẳng zz’ và tt’ cắt nhau tại \(A\). Góc đối đỉnh với \(\widehat {zAt'}\) là:
-
A.
\(\widehat {z'At'}\)
-
B.
\(\widehat {z'At}\)
-
C.
\(\widehat {zAt'}\)
-
D.
\(\widehat {zAt}\)
Cho hai đường thẳng \(xx'\) và \(yy'\) cắt nhau tại \(O\) sao cho \(\widehat {xOy} = 135^\circ \) . Chọn câu đúng:
-
A.
\(\widehat {x'Oy} = 135^\circ \)
-
B.
\(\widehat {x'Oy'} = 45^\circ \)
-
C.
\(\widehat {xOy'} = 135^\circ \)
-
D.
\(\widehat {x'Oy'} = 135^\circ \)
Cho 2 đường thẳng ab và cd cắt nhau tại M ( tia Ma đối tia Mb). Biết \(\widehat {aMc} = 5.\widehat {bMc}\). Tính số đo \(\widehat {aMc}\) ?
-
A.
30\(^\circ \)
-
B.
36\(^\circ \)
-
C.
144\(^\circ \)
-
D.
150\(^\circ \)
Cho \(\widehat {ABC} = {56^o}\). Vẽ \(\widehat {ABC'}\) kề bù với \(\widehat {ABC}\); \(\widehat {C'BA'}\) kề bù với \(\widehat {ABC'}\). Tính số đo \(\widehat {C'BA'}\).
-
A.
124o
-
B.
142o
-
C.
65o
-
D.
56o
Vẽ góc \(xOy\) có số đo bằng 125o. Vẽ góc \(x'Oy'\) đối đỉnh với góc \(xOy.\) Viết tên các góc có số đo bằng 55o.
-
A.
\(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy'}\)
-
B.
\(\widehat {xOy}\,\,;\,\,\widehat {x'Oy'}\)
-
C.
\(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy}\)
-
D.
\(\widehat {xOy'}\,\,;\,\,\widehat {xOy}\)
Cho tia Ok là tia phân giác của \(\widehat {mOn}\)= 70o . Tính \(\widehat {nOk}\)
-
A.
70o
-
B.
140o
-
C.
35o
-
D.
110o
Cho hình vẽ sau. Biết góc $xOy'$ đối đỉnh với góc $x'Oy,$ biết \(\widehat {xOy'} = {\widehat O_1} = {165^o}\). Tính các góc đỉnh O (khác góc bẹt).
-
A.
\({\widehat O_2} = {165^o};\,{\widehat O_3} = {15^o};\,\,{\widehat O_4} = {165^o}\,\,\)
-
B.
\({\widehat O_2} = {165^o};\,{\widehat O_3} = {15^o};\,\,{\widehat O_4} = {15^o}\,\,\)
-
C.
\({\widehat O_2} = {15^o};\,{\widehat O_3} = {15^o};\,\,{\widehat O_4} = {165^o}\,\,\)
-
D.
\({\widehat O_2} = {15^o};\,{\widehat O_3} = {165^o};\,\,{\widehat O_4} = {15^o}\,\,\)
Lời giải và đáp án
Hai đường thẳng zz’ và tt’ cắt nhau tại $A$. Góc đối đỉnh với \(\widehat {zAt'}\) là:
-
A.
\(\widehat {z'At'}\)
-
B.
\(\widehat {z'At}\)
-
C.
\(\widehat {zAt'}\) \(\)
-
D.
\(\widehat {zAt}\)
Đáp án : B
Áp dụng định nghĩa hai góc đối đỉnh, xác định tia đối của tia \(Az\) và \(At'\), từ đó xác định góc đối đỉnh với \(\widehat {zAt'}\).
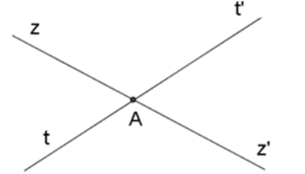
Vì hai đường thẳng $zz'$ và $tt'$ cắt nhau tại $A$ nên $Az'$ là tia đối của tia $Az,At'$ là tia đối của tia $At.$ Vậy góc đối đỉnh với \(\widehat {zAt'}\) là \(\widehat {z'At}\).
Cho góc \(xBy\) đối đỉnh với góc \(x'By'\) và \(\widehat {xBy} = 60^\circ \) . Tính số đo góc \(x'By'.\)
-
A.
$30^\circ$
-
B.
$120^\circ$
-
C.
$90^\circ$
-
D.
$60^\circ$
Đáp án : D
Áp dụng tính chất: Hai góc đối đỉnh thì bằng nhau.
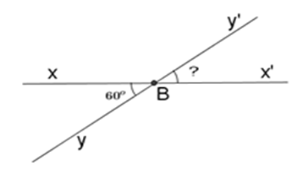
Vẽ \(\widehat {x'By'}\) là góc đối đỉnh với \(\widehat {xBy}\). Khi đó:
\(\widehat {x'By'} = \widehat {xBy} = {60^o}\) (tính chất hai góc đối đỉnh)
Cho hai đường thẳng \(xx'\) và \(yy'\) giao nhau tại \(O\) sao cho \(\widehat {xOy} = 45^\circ \) . Chọn câu sai.
-
A.
$\widehat {x'Oy} = 135^\circ $
-
B.
$\widehat {x'Oy'} = 45^\circ $
-
C.
$\widehat {xOy'} = 135^\circ $
-
D.
$\widehat {x'Oy'} = 135^\circ $
Đáp án : D
+ Sử dụng tính chất: Hai góc đối đỉnh thì bằng nhau
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)
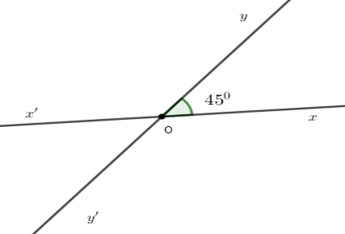
Vì hai đường thẳng $xx'$ và $yy'$ cắt nhau tại $O$ nên $Ox'$ là tia đối của tia $Ox;Oy'$ là tia đối của tia $Oy.$
Suy ra \(\widehat {xOy}\) và \(\widehat {x'Oy'}\) ; \(\widehat {x'Oy}\) và \(\widehat {xOy'}\) là hai cặp góc đối đỉnh.
Do đó \(\widehat {x'Oy'} = \widehat {xOy} = 45^\circ \) và \(\widehat {x'Oy} = \widehat {xOy'}\)
Lại có \(\widehat {xOy}\) và \(\widehat {x'Oy}\) là hai góc ở vị trí kề bù nên \(\widehat {xOy} + \widehat {x'Oy} = 180^\circ \)\( \Rightarrow 45^\circ + \widehat {x'Oy} = 180^\circ \Rightarrow \widehat {x'Oy} = 180^\circ - 45^\circ \)
\( \Rightarrow \widehat {x'Oy} = 135^\circ \)
Vậy \(\widehat {x'Oy'} = \widehat {xOy} = 45^\circ \) và \(\widehat {x'Oy} = \widehat {xOy'} = 135^\circ .\)
Suy ra A, B, C đúng, D sai.
Cho cặp góc đối đỉnh \(\widehat {tOz}\) và \(\widehat {t'Oz'}\) (\(Oz\) và $Oz'$ là hai tia đối nhau). Biết \(\widehat {tOz'} = 4.\widehat {tOz}\). Tính các góc \(\widehat {tOz}\) và \(\widehat {t'Oz'}.\)
-
A.
\(\widehat {zOt} = \widehat {z'Ot'} = 72^\circ \)
-
B.
\(\widehat {zOt} = \widehat {z'Ot'} = 30^\circ \)
-
C.
\(\widehat {zOt} = \widehat {z'Ot'} = 36^\circ \)
-
D.
\(\widehat {zOt} = 72^\circ ;\,\widehat {z'Ot'} = 36^\circ \)
Đáp án : C
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)
+ Sử dụng tính chất: Hai góc đối đỉnh thì bằng nhau
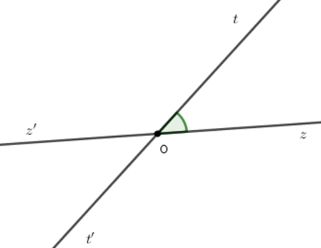
Ta có \(\widehat {zOt} + \widehat {tOz'} = 180^\circ \) (hai góc kề bù) mà \(\widehat {tOz'} = 4.\widehat {tOz}\) \( \Rightarrow \widehat {zOt} + 4.\widehat {zOt} = 180^\circ \) \( \Rightarrow 5.\widehat {zOt} = 180^\circ \Rightarrow \widehat {zOt} = 36^\circ \)
Vì \(\widehat {tOz}\) và \(\widehat {t'Oz'}\) là hai góc đối đỉnh nên \(\widehat {zOt} = \widehat {z'Ot'} = 36^\circ .\)
Vẽ góc $xOy$ có số đo bằng $35^\circ$. Vẽ góc $x'Oy'$ đối đỉnh với góc $xOy.$ Viết tên các góc có số đo bằng $145^o.$
-
A.
\(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy'}\)
-
B.
\(\widehat {xOy}\,\,;\,\,\widehat {x'Oy'}\)
-
C.
\(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy}\)
-
D.
\(\widehat {xOy'}\,\,;\,\,\widehat {xOy}\)
Đáp án : C
Áp dụng tính chất hai góc đối đỉnh, tính chất hai góc kề bù để tính các góc còn lại.
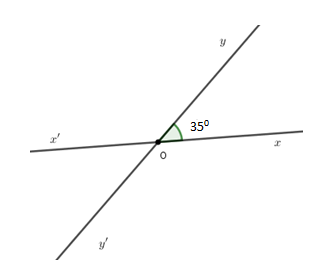
Vì hai đường thẳng $xx'$ và $yy'$ cắt nhau tại $O$ nên $Ox'$ là tia đối của tia $Ox;Oy'$ là tia đối của tia $Oy.$
Suy ra \(\widehat {xOy}\) và \(\widehat {x'Oy'}\) ; \(\widehat {x'Oy}\) và \(\widehat {xOy'}\) là hai cặp góc đối đỉnh.
Do đó \(\widehat {x'Oy'} = \widehat {xOy} = 35^\circ \) và \(\widehat {x'Oy} = \widehat {xOy'}\)
Lại có \(\widehat {xOy}\) và \(\widehat {x'Oy}\) là hai góc ở vị trí kề bù nên \(\widehat {xOy} + \widehat {x'Oy} = 180^\circ \)\( \Rightarrow 35^\circ + \widehat {x'Oy} = 180^\circ \Rightarrow \widehat {x'Oy} = 180^\circ - 35^\circ \)
\( \Rightarrow \widehat {x'Oy} = 145^\circ \)
Vậy \(\widehat {x'Oy'} = \widehat {xOy} = 45^\circ \) và \(\widehat {x'Oy} = \widehat {xOy'} = 145^\circ .\)
Hai góc có số đo bằng ${145^o}$ là : \(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy}\)
Hai đường thẳng \(AB\) và \(CD\) cắt nhau tại $O$ tạo thành \(\widehat {AOC} = 60^\circ \) . Gọi \(OM\) là phân giác \(\widehat {AOC}\) và \(ON\) là tia đối của tia \(OM\). Tính \(\widehat {BON}\) và \(\widehat {DON}.\)
-
A.
\(\widehat {BON} = \widehat {DON} = 25^\circ \)
-
B.
\(\widehat {BON} = \widehat {DON} = 30^\circ \)
-
C.
\(\widehat {BON} = \widehat {DON} = 60^\circ \)
-
D.
\(\widehat {BON} = \widehat {DON} = 45^\circ \)
Đáp án : B
+ Sử dụng tính chất tia phân giác tính các góc \(\widehat {AOM};\widehat {COM}\)
+ Sử dụng tính chất hai góc đối đỉnh để suy ra hai góc \(\widehat {BON}\) và \(\widehat {DON}.\)
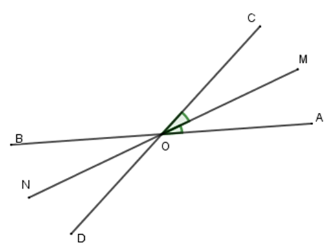
Vì \(AB\) và \(CD\) cắt nhau tại \(O\) nên \(OA\) và \(OB\) là hai tia đối nhau, \(OC\) và \(OD\) là hai tia đối nhau.
Vì \(OM\) là tia phân giác \(\widehat {COA}\) nên \(\widehat {AOM} = \widehat {COM} = \dfrac{{\widehat {COA}}}{2} = \dfrac{{60}}{2} = 30^\circ \)
Mà \(ON\) và \(OM\) là hai tia đối nhau nên \(\widehat {AOM}\) và \(\widehat {BON}\) là hai góc đối đỉnh; \(\widehat {COM}\) và \(\widehat {DON}\) là hai góc đối đỉnh
Suy ra \(\widehat {AOM} = \widehat {BON} = 30^\circ ;\widehat {COM} = \widehat {DON} = 30^\circ \) hay \(\widehat {BON} = \widehat {DON} = 30^\circ .\)
Hai đường thẳng $AB$ và $CD$ cắt nhau tại $O.$ Biết \(\widehat {AOC} - \widehat {AOD} = {50^0}.\) Chọn câu đúng.
-
A.
\(\widehat {AOC} = 110^\circ \)
-
B.
\(\widehat {BOC} = 65^\circ \)
-
C.
\(\widehat {BOD} = 120^\circ \)
-
D.
\(\widehat {AOD} = 50^\circ \)
Đáp án : B
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)
+ Sử dụng tính chất: Hai góc đối đỉnh thì bằng nhau
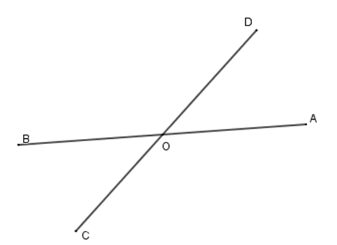
Vì \(\widehat {AOD}\) và \(\widehat {AOC}\) là hai góc kề bù nên \(\widehat {AOD} + \widehat {AOC} = 180^\circ \) mà \(\widehat {AOC} - \widehat {AOD} = 50^\circ \)
Nên \(\widehat {AOC} = \dfrac{{180^\circ + 50^\circ }}{2} = 115^\circ \) và \(\widehat {AOD} = 180^\circ - \widehat {AOC} = 65^\circ \)
Mà \(\widehat {AOD}\) và \(\widehat {BOC}\) là hai góc đối đỉnh nên \(\widehat {BOC} = \widehat {AOD} = 65^\circ .\)
Lại có \(\widehat {BOD}\) và \(\widehat {AOC}\) là hai góc đối đỉnh nên \(\widehat {BOD} = \widehat {AOC} = 115^\circ .\)
Vậy \(\widehat {BOD} = \widehat {AOC} = 115^\circ ;\,\widehat {BOC} = \widehat {AOD} = 65^\circ .\)
Hai đường thẳng zz’ và tt’ cắt nhau tại \(A\). Góc đối đỉnh với \(\widehat {zAt'}\) là:
-
A.
\(\widehat {z'At'}\)
-
B.
\(\widehat {z'At}\)
-
C.
\(\widehat {zAt'}\)
-
D.
\(\widehat {zAt}\)
Đáp án : B
Áp dụng định nghĩa hai góc đối đỉnh, xác định tia đối của tia Az và At, từ đó xác định góc đối đỉnh với \(\widehat {zAt}\).
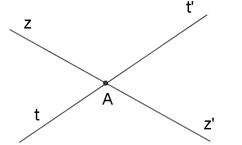
Vì hai đường thẳng \(zz'\) và \(tt'\) cắt nhau tại \(A\) nên \(Az'\) là tia đối của tia \(Az,At'\) là tia đối của tia \(At.\) Vậy góc đối đỉnh với \(\widehat {zAt'}\) là \(\widehat {z'At}\).
Cho hai đường thẳng \(xx'\) và \(yy'\) cắt nhau tại \(O\) sao cho \(\widehat {xOy} = 135^\circ \) . Chọn câu đúng:
-
A.
\(\widehat {x'Oy} = 135^\circ \)
-
B.
\(\widehat {x'Oy'} = 45^\circ \)
-
C.
\(\widehat {xOy'} = 135^\circ \)
-
D.
\(\widehat {x'Oy'} = 135^\circ \)
Đáp án : D
+ Sử dụng tính chất: Hai góc đối đỉnh thì bằng nhau
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)
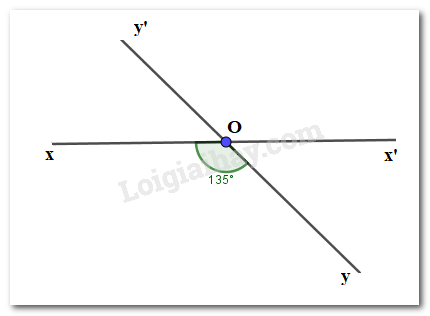
Vì hai đường thẳng \(xx'\) và \(yy'\) cắt nhau tại \(O\) nên \(Ox'\) là tia đối của tia \(Ox;Oy'\) là tia đối của tia \(Oy.\)
Suy ra \(\widehat {xOy}\) và \(\widehat {x'Oy'}\) ; \(\widehat {x'Oy}\) và \(\widehat {xOy'}\) là hai cặp góc đối đỉnh.
Do đó \(\widehat {x'Oy'} = \widehat {xOy} = 135^\circ \) và \(\widehat {x'Oy} = \widehat {xOy'}\)
Lại có \(\widehat {xOy}\) và \(\widehat {x'Oy}\) là hai góc kề bù nên
\(\widehat {xOy} + \widehat {x'Oy} = 180^\circ \)
\(45^\circ + \widehat {x'Oy} = 180^\circ \)
Suy ra \(\widehat {x'Oy} = 180^\circ - 135^\circ = 45^\circ \)
Do đó \(\widehat {x'Oy} = \widehat {xOy'} = 45^\circ .\)
Vậy \(\widehat {x'Oy'} = \widehat {xOy} = 135^\circ \) và \(\widehat {x'Oy} = \widehat {xOy'} = 45^\circ .\)
Cho 2 đường thẳng ab và cd cắt nhau tại M ( tia Ma đối tia Mb). Biết \(\widehat {aMc} = 5.\widehat {bMc}\). Tính số đo \(\widehat {aMc}\) ?
-
A.
30\(^\circ \)
-
B.
36\(^\circ \)
-
C.
144\(^\circ \)
-
D.
150\(^\circ \)
Đáp án : D
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)
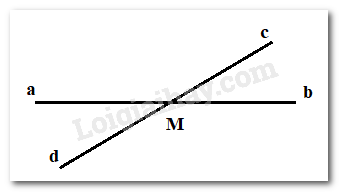
Ta có : \(\widehat {aMc} + \widehat {bMc} = 180^\circ \) ( 2 góc kề bù)
Mà \(\widehat {aMc} = 5.\widehat {bMc}\)
\(\begin{array}{l} \Rightarrow 5.\widehat {bMc} + \widehat {bMc} = 180^\circ \\ \Rightarrow 6.\widehat {bMc} = 180^\circ \\ \Rightarrow \widehat {bMc} = 180^\circ :6 = 30^\circ \\ \Rightarrow \widehat {aMc} = 5.30^\circ = 150^\circ \end{array}\)
\(\begin{array}{l} \Rightarrow 5.\widehat {bMc} + \widehat {bMc} = 180^\circ \\ \Rightarrow 6.\widehat {bMc} = 180^\circ \\ \Rightarrow \widehat {bMc} = 180^\circ :6 = 30^\circ \\ \Rightarrow \widehat {aMc} = 5.30^\circ = 150^\circ \end{array}\)
Cho \(\widehat {ABC} = {56^o}\). Vẽ \(\widehat {ABC'}\) kề bù với \(\widehat {ABC}\); \(\widehat {C'BA'}\) kề bù với \(\widehat {ABC'}\). Tính số đo \(\widehat {C'BA'}\).
-
A.
124o
-
B.
142o
-
C.
65o
-
D.
56o
Đáp án : D
Áp dụng tính chất hai góc kề bù, xác định các tia đối từ đó xác định góc đối đỉnh. Áp dụng tính chất hai góc đối đỉnh để tính góc \(C'BA'.\)
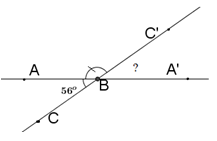
Vì góc \(ABC'\) kề bù với góc \(ABC\) nên \(BC'\) là tia đối của tia \(BC.\)
Vì góc \(C'BA'\) kề bù với góc \(ABC'\) nên \(BA'\) là tia đối của tia \(BA.\)
Do đó, góc \(C'BA'\) và góc \(ABC\) đối đỉnh.
\( \Rightarrow \widehat {C'BA'} = \widehat {ABC} = {56^o}\)
Vẽ góc \(xOy\) có số đo bằng 125o. Vẽ góc \(x'Oy'\) đối đỉnh với góc \(xOy.\) Viết tên các góc có số đo bằng 55o.
-
A.
\(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy'}\)
-
B.
\(\widehat {xOy}\,\,;\,\,\widehat {x'Oy'}\)
-
C.
\(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy}\)
-
D.
\(\widehat {xOy'}\,\,;\,\,\widehat {xOy}\)
Đáp án : C
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)
+ Sử dụng tính chất: Hai góc đối đỉnh thì bằng nhau
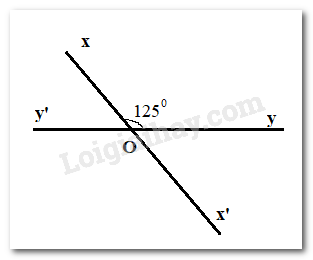
Vì hai đường thẳng \(xx'\) và \(yy'\) cắt nhau tại \(O\) nên \(Ox'\) là tia đối của tia \(Ox;Oy'\) là tia đối của tia \(Oy.\)
Suy ra \(\widehat {xOy}\) và \(\widehat {x'Oy'}\) ; \(\widehat {x'Oy}\) và \(\widehat {xOy'}\) là hai cặp góc đối đỉnh.
Do đó \(\widehat {x'Oy'} = \widehat {xOy} = 125^\circ \) và \(\widehat {x'Oy} = \widehat {xOy'}\)
Lại có \(\widehat {xOy}\) và \(\widehat {x'Oy}\) là hai góc ở vị trí kề bù nên
\(\widehat {xOy} + \widehat {x'Oy} = 180^\circ \)
Suy ra \(125^\circ + \widehat {x'Oy} = 180^\circ \)
Suy ra \(\widehat {x'Oy} = 180^\circ - 125^\circ = 55^\circ \)
Hai góc có số đo bằng 55o là : \(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy}\)
Cho tia Ok là tia phân giác của \(\widehat {mOn}\)= 70o . Tính \(\widehat {nOk}\)
-
A.
70o
-
B.
140o
-
C.
35o
-
D.
110o
Đáp án : C
Sử dụng tính chất tia phân giác của một góc
Vì Ok là tia phân giác của \(\widehat {mOn}\) nên \(\widehat {mOk} = \widehat {nOk} = \frac{1}{2}.\widehat {mOn} = \frac{1}{2}.70^\circ = 35^\circ \)
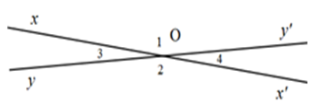
Cho hình vẽ sau. Biết góc $xOy'$ đối đỉnh với góc $x'Oy,$ biết \(\widehat {xOy'} = {\widehat O_1} = {165^o}\). Tính các góc đỉnh O (khác góc bẹt).
-
A.
\({\widehat O_2} = {165^o};\,{\widehat O_3} = {15^o};\,\,{\widehat O_4} = {165^o}\,\,\)
-
B.
\({\widehat O_2} = {165^o};\,{\widehat O_3} = {15^o};\,\,{\widehat O_4} = {15^o}\,\,\)
-
C.
\({\widehat O_2} = {15^o};\,{\widehat O_3} = {15^o};\,\,{\widehat O_4} = {165^o}\,\,\)
-
D.
\({\widehat O_2} = {15^o};\,{\widehat O_3} = {165^o};\,\,{\widehat O_4} = {15^o}\,\,\)
Đáp án : B
Áp dụng tính chất hai góc đối đỉnh, hai góc kề bù để tính các góc còn lại.
\({\widehat O_2} = {\widehat O_1} = {165^o}\) (tính chất hai góc đối đỉnh)
Góc ${O_1}$ và góc ${O_4}$ là hai góc kề bù
\( \Rightarrow {\widehat O_1} + {\widehat O_4} = {180^o}\)
\( \Rightarrow {\widehat O_4} = {180^o} - {\widehat O_1}\)
\( \Rightarrow {\widehat O_4} = {180^o} - {165^o} = {15^o}\)
\({\widehat O_3} = {\widehat O_4} = {15^o}\,\) (hai góc đối đỉnh)
Luyện tập và củng cố kiến thức Bài 2: Tia phân giác của một góc Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 3: Hai đường thẳng song song Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 4: Định lí Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
- Trắc nghiệm Bài 13: Tính chất ba đường cao của tam giác Toán 7 Cánh diều
- Trắc nghiệm Bài 12: Tính chất ba đường trung trực của tam giác Toán 7 Cánh diều
- Trắc nghiệm Bài 11: Tính chất ba đường phân giác của tam giác Toán 7 Cánh diều
- Trắc nghiệm Bài 10: Tính chất ba đường trung tuyến của tam giác Toán 7 Cánh diều
- Trắc nghiệm Bài 9: Đường trung trực của một đoạn thẳng Toán 7 Cánh diều
