Toán 12 Cùng khám phá | Giải toán lớp 12 Cùng khám phá Bài 3. Đường tiệm cận của đồ thị hàm số - Toán 12 Cùng ..

Lý thuyết Đường tiệm cận của đồ thị hàm số Toán 12 Cùng khám phá


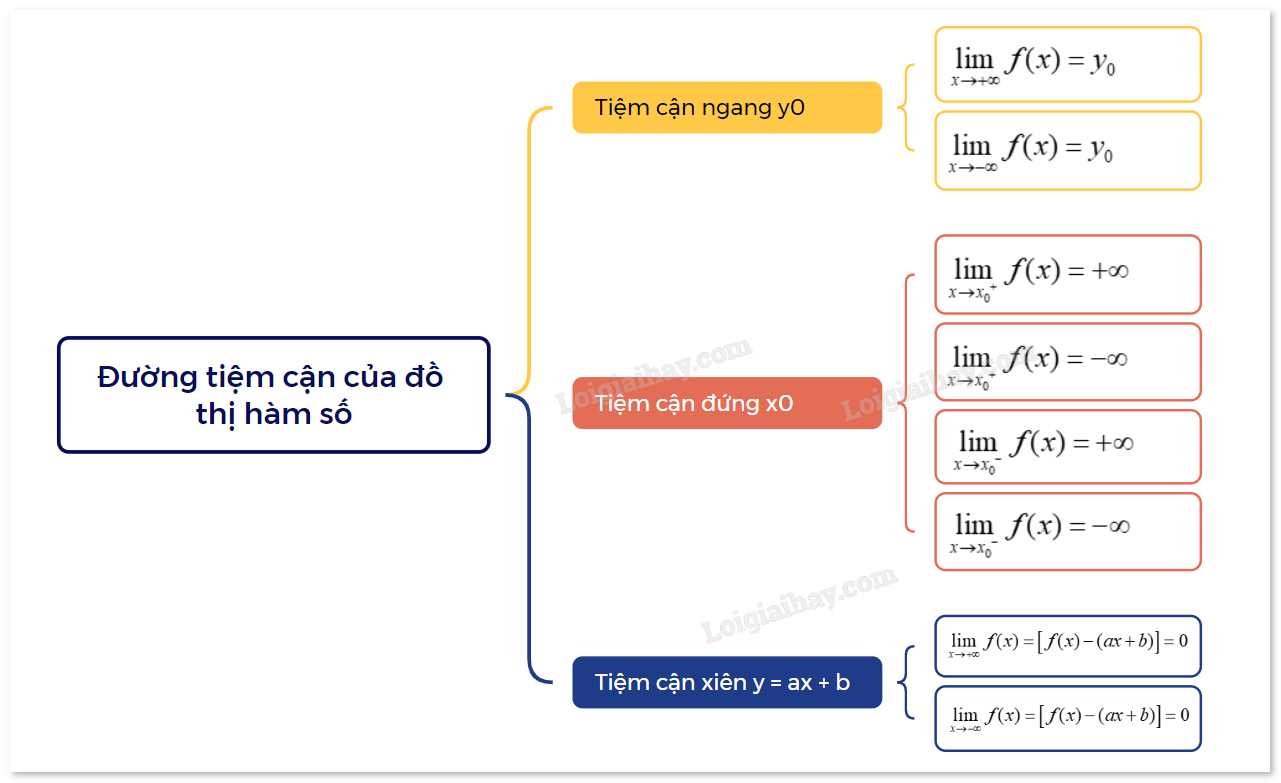
1. Đường tiệm cận ngang của đồ thị hàm số

1. Đường tiệm cận ngang của đồ thị hàm số

Đường thẳng \(y = {y_0}\) gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to  + \infty } f(x) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to  - \infty } f(x) = {y_0}\).

Ví dụ: Tìm TCN của đồ thị hàm số \(y = f(x) = \frac{{3x - 2}}{{x + 1}}\).

Ta có: \(\mathop {\lim }\limits_{x \to  + \infty } \frac{{3x - 2}}{{x + 1}} = \mathop {\lim }\limits_{x \to  - \infty } \frac{{3x - 2}}{{x + 1}} = 3\).

Vậy đồ thị hàm số f(x) có TCN là y = 3.

2. Đường tiệm cận đứng của đồ thị hàm số

Đường thẳng \(x = {x_0}\) gọi là đường tiệm cận đứng (gọi tắt là tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:\(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) =  + \infty ;\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) =  - \infty ;\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) =  + \infty ;\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) =  - \infty \).

Ví dụ: Tìm TCĐ của đồ thị hàm số \(y = f(x) = \frac{{3 - x}}{{x + 2}}\).

Ta có: \(\mathop {\lim }\limits_{x \to  - {2^ + }} \frac{{3x - 2}}{{x + 2}} =  + \infty \).

Vậy đồ thị hàm số có TCĐ là x = -2.

3. Đường tiệm cận xiên của đồ thị hàm số

Đường thẳng \(y = ax + b(a \ne 0)\) gọi là đường tiệm cận xiên (gọi tắt là tiệm cận xiên) của đồ thị hàm số y = f(x) nếu

\(\mathop {\lim }\limits_{x \to  + \infty } f(x) = \left[ {f(x) - (ax + b)} \right] = 0\)

hoặc \(\mathop {\lim }\limits_{x \to  - \infty } f(x) = \left[ {f(x) - (ax + b)} \right] = 0\).

Ví dụ: Tìm TCX của đồ thị hàm số \(y = f(x) = x + \frac{1}{{x + 2}}\).

Ta có: \(\mathop {\lim }\limits_{x \to  + \infty } \left[ {f(x) - x} \right] = \mathop {\lim }\limits_{x \to  + \infty } \frac{1}{{x + 2}} = 0\).

Vậy đồ thị hàm số có TCX là y = x.


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo
  • Giải mục 1 trang 15, 16 SGK Toán 12 tập 1 - Cùng khám phá

    Cho hàm số \(y = f(x) = \frac{{x + 1}}{{x + 2}}\) có đồ thị (C) là đường cong ( Hình 1.12). Nêu nhận xét về khoảng cách từ điểm \(M(x;y) \in (C)\)M(x;y) tới đường thẳng y=1 khi \(x \to + \infty \) và \(x \to - \infty \).

  • Giải mục 2 trang 17, 18 SGK Toán 12 tập 1 - Cùng khám phá

    Cho hàm số \(y = \frac{{x + 1}}{{x - 2}}\)có đồ thị (C ) như Hình 1.17. a) Nêu nhận xét về khoảng cách từ điểm \(M(x;y) \in (C)\)đến đường thảng x=2 khi \(x \to 2\) b) Tính các giới hạn \(\mathop {\lim }\limits_{x \to {2^ + }} f(x)\) và \(\mathop {\lim }\limits_{x \to {2^ - }} f(x)\)

  • Giải mục 3 trang 19, 20, 21 SGK Toán 12 tập 1 - Cùng khám phá

    Trong Hình 1.21, đường cong là đồ thị ( C ) của hàm số (y = f(x) = x + frac{x}{{{x^2} - 1}}) và đường thẳng (Delta :y = x) . Gọi M, N lần lượt là hai điểm thuộc ( C ) và(Delta ) có cùng hoành độ x, với x > 1 hoặc x < -1. Nhận xét về độ dài của đoạn MN khi(x to - infty ) và (x to + infty )

  • Giải bài tập 1.14 trang 21 SGK Toán 12 tập 1 - Cùng khám phá

    Cho hàm số (y = frac{{2x + 1}}{{x + 1}}) có đồ thị là đường cong như hình 1.26. Xác định phương trình đường tiệm cận đứng, đường tiệm cận ngang của hàm số.

  • Giải bài tập 1.15 trang 21 SGK Toán 12 tập 1 - Cùng khám phá

    Xác định các đường tiệm cận đứng của các đồ thị hàm số \(y = \tan x\) ( hình 1.27a) và \(y = \cot x\) (hình 1.27b).

>> Xem thêm

Báo lỗi - Góp ý

Group Ôn Thi ĐGNL & ĐGTD Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store