 Toán 12 Cùng khám phá | Giải toán lớp 12 Cùng khám phá
Toán 12 Cùng khám phá | Giải toán lớp 12 Cùng khám phá
 Bài 3. Đường tiệm cận của đồ thị hàm số - Toán 12 Cùng ..
Bài 3. Đường tiệm cận của đồ thị hàm số - Toán 12 Cùng ..
Giải mục 3 trang 19, 20, 21 SGK Toán 12 tập 1 - Cùng khám phá
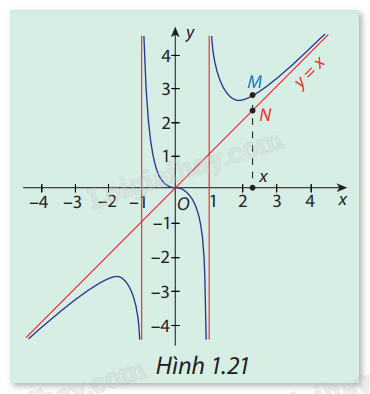
Trong Hình 1.21, đường cong là đồ thị ( C ) của hàm số (y = f(x) = x + frac{x}{{{x^2} - 1}}) và đường thẳng (Delta :y = x) . Gọi M, N lần lượt là hai điểm thuộc ( C ) và(Delta ) có cùng hoành độ x, với x > 1 hoặc x < -1. Nhận xét về độ dài của đoạn MN khi(x to - infty ) và (x to + infty )
HĐ3
Trả lời câu hỏi Hoạt động 3 trang 19 SGK Toán 12 Cùng khám phá
Trong Hình 1.21, đường cong là đồ thị ( C ) của hàm số \(y = f(x) = x + \frac{x}{{{x^2} - 1}}\) và đường thẳng \(\Delta :y = x\) . Gọi M, N lần lượt là hai điểm thuộc ( C ) và\(\Delta \) có cùng hoành độ x, với x > 1 hoặc x < -1. Nhận xét về độ dài của đoạn MN khi\(x \to - \infty \) và \(x \to + \infty .\)
Phương pháp giải:
Nhìn vào đồ thị rồi nhận xét.
Lời giải chi tiết:
Khi \(x \to - \infty \) và \(x \to + \infty \) thì độ dài MN càng ngắn.
LT3
Trả lời câu hỏi Luyện tập 3 trang 20 SGK Toán 12 Cùng khám phá
Sử dụng ghi chú ở trên, tìm tiệm cận xiên của đồ thị hàm số \(y = f(x) = \frac{{ - {x^2} - 3x - 3}}{{x + 1}}\).
Phương pháp giải:
Phân tích hàm số rồi áp dụng ghi chú: hàm số \(y = \frac{{a{x^2} + bx + c}}{{mx + n}}\) (\(a \ne 0,m \ne 0\) đa thức tử không chia hết cho đa thức mẫu) luôn được viết dưới dạng \(y = px + q + \frac{r}{{mx + n}}\)\((p,q,r \in R)\).Khi đó đồ thị hàm số có đường tiệm cận đứng \(x = - \frac{n}{m}\)là và đường tiệm cận xiên là \(y = px + q.\)
Lời giải chi tiết:
Ta có \(y = f(x) = \frac{{ - {x^2} - 3x - 3}}{{x + 1}}\)\( = - x - 2 - \frac{1}{{x + 1}}.\)
Áp dụng ghi chú hàm số \(y = \frac{{a{x^2} + bx + c}}{{mx + n}}\) (\(a \ne 0,m \ne 0\) đa thức tử không chia hết cho đa thức mẫu) luôn được viết dưới dạng \(y = px + q + \frac{r}{{mx + n}}\)\((p,q,r \in R)\).Khi đó đồ thị hàm số có đường tiệm cận xiên là \(y = px + q\), khi đó đường tiệm cận xiên của hàm số là \(y = - x - 2.\)
VD1
Trả lời câu hỏi Vận dụng 1 trang 20 SGK Toán 12 Cùng khám phá
Trong phần Khởi động đầu bài, tìm đường tiệm cận đứng của đồ thị hàm số \(m(v) = \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\), từ đó nhận xét khối lượng của vật khi vận tốc của nó càng gần vận tốc ánh sáng.
Phương pháp giải:
Tìm giới hạn của khối lượng m(v) khi vận tốc v tiến gần đến tốc độ ánh sáng c.
Lời giải chi tiết:
Xét \(m(v) = \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\).
Tập xác định: \(D = \mathbb{N}\backslash \{ c\} \).
Ta có: \(\mathop {\lim }\limits_{v \to {c^ + }} m(v) = \mathop {\lim }\limits_{v \to {c^ + }} \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }} = \mathop {\lim }\limits_{v \to {c^ + }} \frac{{\frac{{{m_0}}}{v}}}{{\sqrt {\frac{1}{{{v^2}}} - \frac{1}{{{c^2}}}} }} = \frac{{\frac{{{m_0}}}{c}}}{{\sqrt {\frac{1}{{{c^2}}} - \frac{1}{{{c^2}}}} }} = + \infty .\)
\(\mathop {\lim }\limits_{v \to c - } m(v) = \mathop {\lim }\limits_{v \to {c^ - }} \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }} = \mathop {\lim }\limits_{v \to c - } \frac{{\frac{{{m_0}}}{v}}}{{\sqrt {\frac{1}{{{v^2}}} - \frac{1}{{{c^2}}}} }} = \frac{{\frac{{{m_0}}}{c}}}{{\sqrt {\frac{1}{{{c^2}}} - \frac{1}{{{c^2}}}} }} = + \infty .\)
Vậy đường thẳng x = c là tiệm cận đứng của đồ thị hàm số. Khi vận tốc của vật tiến dần đến tốc độ ánh sáng, khối lượng của vật càng lớn.
VD2
Trả lời câu hỏi Vận dụng 2 trang 21 SGK Toán 12 Cùng khám phá
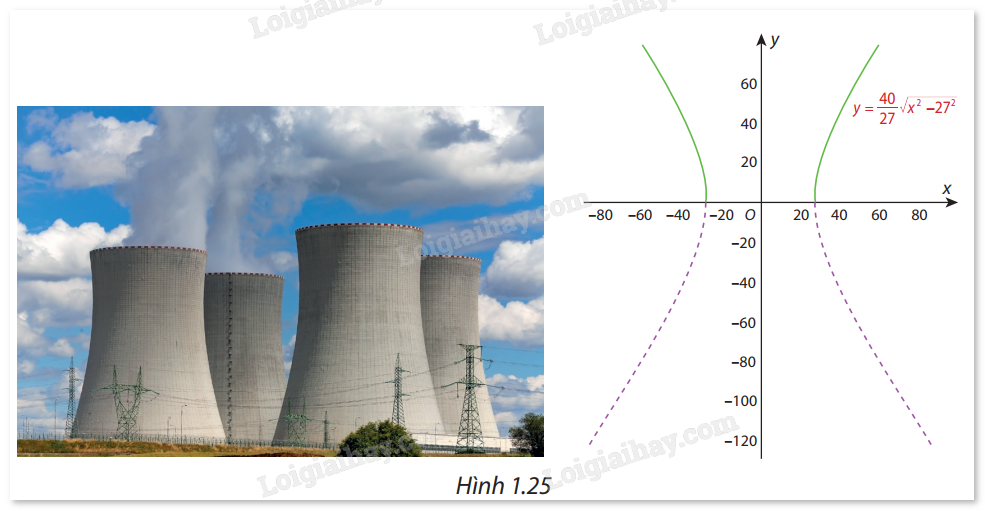
Một ống khói của nhà máy điện hạt nhân có mặt cắt là một hypebol (H) có phương trình chính tắc là \(\frac{{{x^2}}}{{{{27}^2}}} - \frac{{{y^2}}}{{{{40}^2}}} = 1\) (Hình 1.25). Hét hai nhánh bên trên Ox của (H) là đồ thị (C) của hàm số \(y = \frac{{40}}{{27}}\sqrt {{x^2} - {{27}^2}} \) (phần nét liền đậm). Chứng minh rằng đường thẳng \(y = \frac{{40}}{{27}}x\) là một đường tiệm cận của (C). Hãy chỉ ra them một đường tiệm cận xiên khác của (C).
Phương pháp giải:
Chứng minh \(\mathop {\lim }\limits_{x \to + \infty } \left( {\frac{{40}}{{27}}\sqrt {{x^2} - {{27}^2}} - \frac{{40}}{{27}}x} \right) = 0\).
Lời giải chi tiết:
\(\mathop {\lim }\limits_{x \to + \infty } \left( {\frac{{40}}{{27}}\sqrt {{x^2} - {{27}^2}} - \frac{{40}}{{27}}x} \right) = \mathop {\lim }\limits_{x \to + \infty } \left[ {\frac{{40}}{{27}}\left( {\sqrt {{x^2} - {{27}^2}} - x} \right)} \right] = \frac{{40}}{{27}}\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} - {{27}^2}} - x} \right)\)
\( = \frac{{40}}{{27}}\mathop {\lim }\limits_{x \to + \infty } \frac{{40}}{{27}}.\frac{{{x^2} - {{27}^2} - {x^2}}}{{\sqrt {{x^2} - {{27}^2}} + x}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{40}}{{27}}.\left( {\frac{{ - {{27}^2}}}{{\sqrt {{x^2} - {{27}^2}} + x}}} \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 40.27}}{{\sqrt {{x^2} - {{27}^2}} + x}}\)
\( = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 40.27}}{{x\sqrt {1 - \frac{{{{27}^2}}}{{{x^2}}}} + x}} = 0.\)
Vậy \(y = \frac{{40}}{{27}}x\) là tiệm cận xiên của (C).
Tương tự, một tiệm cận xiên khác của (C) là \(y = - \frac{{40}}{{27}}x\).
- Giải bài tập 1.14 trang 21 SGK Toán 12 tập 1 - Cùng khám phá
- Giải bài tập 1.15 trang 21 SGK Toán 12 tập 1 - Cùng khám phá
- Giải bài tập 1.16 trang 22 SGK Toán 12 tập 1 - Cùng khám phá
- Giải bài tập 1.17 trang 22 SGK Toán 12 tập 1 - Cùng khám phá
- Giải bài tập 1.18 trang 22 SGK Toán 12 tập 1 - Cùng khám phá
>> Xem thêm
Các bài khác cùng chuyên mục
- Giải bài tập 6.20 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.19 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.18 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.17 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.16 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.20 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.19 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.18 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.17 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.16 trang 107 SGK Toán 12 tập 2 - Cùng khám phá












Danh sách bình luận