-
Toán 9 tập 1 - Chân trời sáng tạo
-
Toán 9 tập 2 - Chân trời sáng tạo
Toán 9 chân trời sáng tạo | Giải toán lớp 9 chân trời sáng tạo
Bài 4. Hình quạt tròn và hình vành khuyên - Toán 9 Chân..
Giải mục 2 trang 99, 100 SGK Toán 9 tập 1 - Chân trời sáng tạo
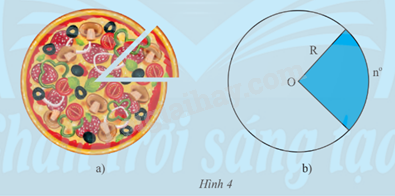
a) Ta có thể tính diện tích của miếng pizza trong Hình 4a theo góc ở tâm và bán kính của ổ bánh hay không? b) Chia một hình tròn bán kính R thành 360 phần bằng nhau. i) Tính diện tích mỗi phần đó. ii) Tính diện tích phần hình tròn ghép bởi n phần bằng nhau nó trên (Hình 4b).
HĐ2
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 99 SGK Toán 9 Chân trời sáng tạo
a) Ta có thể tính diện tích của miếng pizza trong Hình 4a theo góc ở tâm và bán kính của ổ bánh hay không?
b) Chia một hình tròn bán kính R thành 360 phần bằng nhau.
i) Tính diện tích mỗi phần đó.
ii) Tính diện tích phần hình tròn ghép bởi n phần bằng nhau nó trên (Hình 4b).
Phương pháp giải:
Dựa vào công thức diện tích hình tròn: S =\(\pi \)R2 .
Lời giải chi tiết:
a) Ta có thể tính diện tích của miếng pizza trong Hình 4a theo góc ở tâm và bán kính của ổ bánh.
b) i) Chia một hình tròn bán kính R thành 360 phần bằng nhau, diện tích mỗi phần đó là: \(\frac{{\pi {R^2}}}{{360}}\).
ii) diện tích phần hình tròn ghép bởi n phần bằng nhau là: \(n.\frac{{\pi {R^2}}}{{360}}\)
TH2
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 2 trang 100 SGK Toán 9 Chân trời sáng tạo
Tính diện tích hình quạt tròn với bán kính R = 20 cm, ứng với cung 72o.
Phương pháp giải:
Dựa vào công thức hình quạt tròn: \(S = \frac{{\pi {R^2}n}}{{360}}\)
Lời giải chi tiết:
Hình quạt tròn với bán kính R = 20 cm, ứng với cung 72o có diện tích là:
\(S = \frac{{\pi {R^2}n}}{{360}} = \frac{{\pi {{.20}^2}.72}}{{360}} \approx 251,33\)(cm2)
VD2
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 2 trang 100 SGK Toán 9 Chân trời sáng tạo
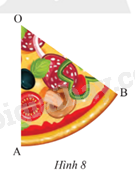
Tính diện tích của miếng bánh pizza có dạng hình quạt tròn trong Hình 8. Biết OA = 15 cm và \(\widehat {AOB} = {55^o}\).
Phương pháp giải:
Dựa vào công thức hình quạt tròn: \(S = \frac{{\pi {R^2}n}}{{360}}\)
Lời giải chi tiết:
Ta có độ dài cung AB = \(\widehat {AOB} = {55^o}\), bán kính R = 15 m có độ dài là:
\(S = \frac{{\pi {R^2}n}}{{360}} = \frac{{\pi {{.15}^2}.55}}{{360}} \approx 108\) cm2.
Bình luận
Chia sẻ
- Giải mục 3 trang 101 SGK Toán 9 tập 1 - Chân trời sáng tạo
- Giải bài tập 1 trang 102 SGK Toán 9 tập 1 - Chân trời sáng tạo
- Giải bài tập 2 trang 102 SGK Toán 9 tập 1 - Chân trời sáng tạo
- Giải bài tập 3 trang 102 SGK Toán 9 tập 1 - Chân trời sáng tạo
- Giải bài tập 4 trang 102 SGK Toán 9 tập 1 - Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Chân trời sáng tạo - Xem ngay
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
