Toán 9 cùng khám phá | Giải toán lớp 9 cùng khám phá Bài 2. Phương trình và hệ hai phương trình bậc nhất hai..

Giải mục 1 trang 8, 9 SGK Toán 9 tập 1 - Cùng khám phá


a) Số tuổi của anh là \(x\), số tuổi của em là \(y\). Lập một hệ thức biểu diễn sự liên hệ giữa \(x\) và \(y\), biết anh lớn hơn em 5 tuổi. b) 500 kg gạo được chia thành \(x\) bao 50 kg và \(y\) bao 20 kg. Lập một hệ thức biểu diễn sự liên hệ giữa \(x\) và \(y\).

Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn

Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa - GDCD

Lựa chọn câu để xem lời giải nhanh hơn

HĐ1

Trả lời câu hỏi Hoạt động 1 trang 8 SGK Toán 9 Cùng khám phá

a) Số tuổi của anh là \(x\), số tuổi của em là \(y\). Lập một hệ thức biểu diễn sự liên hệ giữa \(x\) và \(y\), biết anh lớn hơn em 5 tuổi.

b) 500 kg gạo được chia thành \(x\) bao 50 kg và \(y\) bao 20 kg. Lập một hệ thức biểu diễn sự liên hệ giữa \(x\) và \(y\).

Phương pháp giải:

Dựa vào các mối liên hệ giữa \(x\) và \(y\) để lập hệ thức.

Lời giải chi tiết:

a) Do anh lớn hơn em 5 tuổi nên ta có hệ thức biểu diễn sự liên hệ giữa \(x\) và \(y\) là: \(x - y = 5\).

b) Do 500 kg gạo được chia thành \(x\) bao 50 kg và \(y\) bao 20 kg nên ta có hệ thức biểu diễn sự liên hệ giữa \(x\) và \(y\) là: \(50x + 20y = 500\).

LT1

Trả lời câu hỏi Luyện tập 1 trang 8 SGK Toán 9 Cùng khám phá

Chỉ ra các phương trình bậc nhất hai ẩn \(x\) và \(y\) trong các phương trình sau:

\(\begin{array}{l}5y - x =  - 2;\\3{x^2} - 10y = 1;\\\frac{{{x^2}}}{{x + 1}} - y = 0;\\x + 0y = 4;\\{y^2} - 9x =  - 6.\end{array}\)

Phương pháp giải:

Dựa vào định nghĩa phương trình bậc nhất hai ẩn \(x\) và \(y\)  để xác định.

Lời giải chi tiết:

Các phương trình bậc nhất hai ẩn \(x\) và \(y\) là: \(5y - x =  - 2;\,\,x + 0y = 4\).

HĐ2

Trả lời câu hỏi Hoạt động 2 trang 9 SGK Toán 9 Cùng khám phá

a) Cặp số \(\left( {x_1^{};y_1^{}} \right) = \left( {8;5} \right)\) có thỏa mãn \(50x_1^{} + 20y_1^{} = 500\) không?

b) Tìm một cặp số \(\left( {x_2^{};y_2^{}} \right)\) khác cặp số \(\left( {8;5} \right)\) sao cho \(50x_2^{} + 20y_2^{} = 500\).

c) Tìm một cặp số \(\left( {x_3^{};y_3^{}} \right)\) sao cho \(50x_3^{} + 20y_3^{} \ne 500\).

Phương pháp giải:

a) Thay cặp số vào phương trình để kiểm tra.

b) Thay \(x\) vào phương trình để tìm \(y\) rồi xác định cặp số.

c) Cho một cặp số khác 2 cặp số vừa tìm được.

Lời giải chi tiết:

a) Vì \(50.8 + 20.5 = 500\) nên cặp số \(\left( {8;5} \right)\) thỏa mãn \(50x_1^{} + 20y_1^{} = 500\).

b) Thay \(y_2^{} = 10\) vào phương trình ta được:

\(\begin{array}{l}50x_2^{} + 20.10 = 500\\50x_2^{} = 300\\x_2^{} = 6\end{array}\)

Vậy cặp số \(\left( {6;10} \right)\) là một cặp số thỏa mãn \(50x_2^{} + 20y_2^{} = 500\).

c) Vì \(50.8 + 20.3 \ne 500\) nên cặp số \(\left( {8;3} \right)\) thỏa mãn \(50x_3^{} + 20y_3^{} \ne 500\).

LT2

Trả lời câu hỏi Luyện tập 2 trang 9 SGK Toán 9 Cùng khám phá

Tìm bốn nghiệm của phương trình \(3x - 4y = 5\).

Phương pháp giải:

Tìm cặp số thỏa mãn phương trình để kết luận nghiệm.

Lời giải chi tiết:

+ Vì \(3.1 - 4.\frac{{ - 1}}{2} = 5\) nên cặp số \(\left( {1; - \frac{1}{2}} \right)\) là một nghiệm của phương trình \(3x - 4y = 5\).

+ Vì \(3.2 - 4.\frac{1}{4} = 5\) nên cặp số \(\left( {2;\frac{1}{4}} \right)\) là một nghiệm của phương trình \(3x - 4y = 5\).

+ Vì \(3.3 - 4.1 = 5\) nên cặp số \(\left( {3;1} \right)\) là một nghiệm của phương trình \(3x - 4y = 5\).

+ Vì \(3.4 - 4.\frac{7}{4} = 5\) nên cặp số \(\left( {4;\frac{7}{4}} \right)\) là một nghiệm của phương trình \(3x - 4y = 5\).

LT3

Trả lời câu hỏi Luyện tập 3 trang 9 SGK Toán 9 Cùng khám phá

Trong mặt phẳng tọa độ \(Oxy\), hãy biểu diễn các nghiệm của mỗi phương trình sau:

a) \(4x - y = 3\)

b) \(0x - 2y = 5\)

c) \(7x + 0y = 21\)

Phương pháp giải:

+ Biểu diễn \(x\) theo \(y\) hoặc \(y\) theo \(x\).

+ Tìm hai cặp số là nghiệm của phương trình.

+ Vẽ đồ thị.

Lời giải chi tiết:

a) Xét phương trình \(4x - y = 3\).      (1)

Chuyển vế, ta có \(y = 4x - 3\).

Nếu cho \(x\) một giá trị bất kì thì cặp số \(\left( {x;y} \right)\), trong đó \(y = 4x - 3\), là một nghiệm của phương trình (1) có các nghiệm là \(\left\{ \begin{array}{l}x \in \mathbb{R}\\y = 4x - 3.\end{array} \right.\)

Trong mặt phẳng tọa độ \(Oxy\), tập hợp các điểm biểu diễn các nghiệm của phương trình (1) là đường thẳng \(y = 4x - 3\).

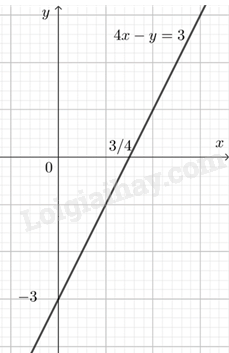
b) Xét phương trình \(0x - 2y = 5\).      (2)

Từ (2), ta có \(2y = 5\) hay \(y = \frac{5}{2}\).

Nếu cho \(x\) một giá trị bất kì thì cặp số \(\left( {x;y} \right)\), trong đó \(y = \frac{5}{2}\), là một nghiệm của phương trình (2).

Do đó phương trình (2) có các nghiệm là \(\left\{ \begin{array}{l}x \in \mathbb{R}\\y = \frac{5}{2}.\end{array} \right.\)

Trong mặt phẳng tọa độ \(Oxy\), tập hợp các điểm biểu diễn các nghiệm của phương trình (2) là đường thẳng đi qua điểm \(A\left( {0;\frac{5}{2}} \right)\) và song song với trục hoành (ta gọi đường thẳng này là đường thẳng \(y = \frac{5}{2}\)).

c) Xét phương trình \(7x + 0y = 21\).        (3)

Từ (3), ta có \(7x = 21\) hay \(x = 3\).

Nếu cho \(y\) một giá trị bất kì thì cặp số \(\left( {x;y} \right)\), tron đó \(x = 3\), là một nghiệm của phương trình (3).

Do đó phương trình (3) có các nghiệm là: \(\left\{ \begin{array}{l}x = 3\\y \in \mathbb{R}.\end{array} \right.\)

Trong mặt phẳng tọa độ \(Oxy\), tập hợp các điểm biểu diễn các nghiệm của phương trình (3) là đường thẳng đi qua điểm \(B\left( { - 3;0} \right)\) và song song với trục tung (ta gọi đường thẳng này là đường thẳng \(x = 3\)).

 


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo
  • Giải mục 2 trang 10, 11, 12 SGK Toán 9 tập 1 - Cùng khám phá

    Trong phần Khởi động, gọi \(x\) (phút) và \(y\) (phút) lần lượt là thời gian cô Dung thực hiện bài thể dục nhịp điệu và bài tập thể dục giãn cơ để đạt được mục tiêu. Lập hai phương trình biểu diễn sự liên hệ giữa \(x\) và \(y\).

  • Giải mục 3 trang 12, 13, 14 SGK Toán 9 tập 1 - Cùng khám phá

    Xét hệ phương trình: \(\left\{ \begin{array}{l}x - 2y = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\ - 3x + 5y = - 4.\,\,\,\,\,\left( 2 \right)\end{array} \right.\) a) Từ phương trình (1) của hệ, biểu diễn \(x\) theo \(y\) rồi thế vào phương trình (2) để được một phương trình mới (chỉ còn một ẩn \(y\)). b) Giải phương trình chỉ còn một ẩn \(y\) ở câu a. c) Thay giá trị của \(y\) tìm được trong câu b vào phương trình biểu diễn \(x\) theo \(y\) trong câu a để tìm giá trị của \(x\). Kiểm

  • Giải mục 4 trang 14, 15, 16 SGK Toán 9 tập 1 - Cùng khám phá

    Xét hệ phương trình: \(\left\{ \begin{array}{l}2x - y = 1\,\,\,\,\,\,\left( 1 \right)\\x + 3y = 4.\,\,\,\,\,\left( 2 \right)\end{array} \right.\) a) Viết phương trình \(\left( {1'} \right)\) thu được khi nhân hai vế của phương trình (1) với 3. b) Cộng từng vế hai phương trình \(\left( {1'} \right)\) và (2) ta được phương trình nào? c) Giải phương trình thu được trong câu b để tìm giá trị của ẩn \(x\). d) Thay giá trị của \(x\) tìm được trong câu c vào phương trình (1) hoặc (2) để tìm giá

  • Giải mục 5 trang 17 SGK Toán 9 tập 1 - Cùng khám phá

    Sử dụng máy tính cầm tay thích hợp, tìm nghiệm của các hệ phương trình sau: a) \(\left\{ \begin{array}{l}9x - 5y = - 11\\22x + 17y = 3;\end{array} \right.\) b) \(\left\{ \begin{array}{l}\frac{2}{5}x - \frac{3}{8}y = \frac{1}{4}\\ - \frac{4}{5}x + \frac{9}{8}y = \frac{7}{8}\end{array} \right.\) c) \(\left\{ \begin{array}{l}0,6x - 0,7y = 1,5\\ - 0,2x + 0,3y = - 1\end{array} \right.\)

  • Giải bài tập 1.8 trang 18 SGK Toán 9 tập 1 - Cùng khám phá

    Tìm ba nghiệm cho mỗi phương trình bậc nhất hai ẩn sau: a) \(5x + 7y = 10\); b) \(11x - 3y = 18\).

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K9 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua