 KHTN 9 Chân trời sáng tạo | Giải Khoa học tự nhiên 9 hay nhất
KHTN 9 Chân trời sáng tạo | Giải Khoa học tự nhiên 9 hay nhất
 Chủ đề 1. Năng lượng cơ học - KHTN 9 Chân trời sáng tạo
Chủ đề 1. Năng lượng cơ học - KHTN 9 Chân trời sáng tạo Bài 3. Công và công suất trang 14, 15, 16 Khoa học tự nhiên 9 Chân trời sáng tạo
Cần cẩu được dùng để nâng các kiện hàng từ dưới thấp lên cao hoặc bốc dỡ các kiện hàng từ trên cao xuống vị trí thấp hơn. Làm thế nào để biết cần cẩu nào hoàn thành công việc nhanh hơn?
Tổng hợp đề thi học kì 1 lớp 9 tất cả các môn - Chân trời sáng tạo
Toán - Văn - Anh - KHTN - Lịch sử và Địa lí
Câu hỏi tr 14 CHMĐ
Trả lời câu hỏi mở đầu trang 14 SGK KHTN 9 Chân trời sáng tạo
Cần cẩu được dùng để nâng các kiện hàng từ dưới thấp lên cao hoặc bốc dỡ các kiện hàng từ trên cao xuống vị trí thấp hơn. Làm thế nào để biết cần cẩu nào hoàn thành công việc nhanh hơn?
Phương pháp giải:
Vận dụng kiến thức về đời sống: Trong cùng một khoảng thời gian, vật nào làm được việc nhiều hơn thì vật đó sẽ hoàn thành công việc nhanh hơn.
Lời giải chi tiết:
Trong cùng một khoảng thời gian, cần cẩu nào nâng các kiện hàng và bốc dỡ nhiều hơn thì cần cẩu đó hoàn thành công việc nhanh hơn.
Câu hỏi tr 14 CH
Trả lời câu hỏi trang 14 SGK KHTN 9 Chân trời sáng tạo
Trong đời sống hằng ngày, người ta thường nói người nông dân gặt lúa, nhân viên thu ngân làm việc tại quầy, học sinh ngồi làm bài tập… đều đang “tốn công sức”. Đó có phải là công cơ học không? Vì sao?
Phương pháp giải:
Vận dụng kiến thức đã học về công cơ học: lực đã thực hiện một công cơ học khi lực đó tác dụng lên vật làm vật đó dịch chuyển một quãng đường theo hướng của lực.
Lời giải chi tiết:
Công cơ học sinh ra từ một lực tương tác với một vật và làm vật đó di chuyển được một quãng đường theo hướng của lực. Các ví dụ trên đều không phải công cơ học vì:
- Người nông dân gặt lúa: gặt là tác động làm cắt rời lúa.
- Nhân viên thu ngân làm việc tại quầy: không có lực tác dụng làm vật nào chuyển động theo hướng của lực.
- Học sinh ngồi làm bài tập: không có lực tác dụng làm vật nào chuyển động theo hướng của lực.
Câu hỏi tr 15 CH 1
Trả lời câu hỏi 1 trang 15 SGK KHTN 9 Chân trời sáng tạo
Nếu lực tác dụng lên vật có phương vuông góc với hướng dịch chuyển của vật thì công thực hiện bởi lực đó bằng bao nhiêu ?
Phương pháp giải:
Vận dụng kiến thức đã học về lực và kiến thức kinh nghiệm đời sống.
- Đưa ra một vài ví dụ về các lực có phương vuông góc với hướng dịch chuyển của vật: trọng lực,…
Lời giải chi tiết:
Nếu lực tác dụng lên vật có phương vuông góc với hướng dịch chuyển của vật thì công thực hiện bởi lực đó bằng không.
Câu hỏi tr 15 LT
Trả lời câu hỏi luyện tập trang 15 SGK KHTN 9 Chân trời sáng tạo
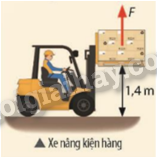
Một xe nâng tác dụng một lực hướng lên, có độ lớn 2 000 N để nâng kiện hàng từ mặt đất lên độ cao 1,4 m. Tính công của lực nâng.
Phương pháp giải:
Vận dụng kiến thức đã học về công cơ học: \(A = F.s\)
Lời giải chi tiết:
Công của lực nâng này là :
A = F.s = 2 000.1,4 = 2 800 (J)
Câu hỏi tr 15 CH 2
Trả lời câu hỏi 2 trang 15 SGK KHTN 9 Chân trời sáng tạo
Trong tình huống đã nêu, nếu xét trong một phút thì máy cày nào thực hiện công lớn hơn?
Phương pháp giải:
Vận dụng kiến thức đã học về công cơ học: \(A = F.s\)
Lời giải chi tiết:
Trong 1 phút, máy A cày được:
\(\frac{2}{{30}} = \frac{1}{{15}}{\rm{ }}\) (mẫu)
Trong 1 phút, máy B cày được \(\frac{1}{{10}}{\rm{ }}\) (mẫu)
Như vậy, trong 1 phút, máy B thực hiện công lớn hơn.
Câu hỏi tr 16 LT
Trả lời câu hỏi luyện tập trang 16 SGK KHTN 9 Chân trời sáng tạo
Cần cẩu A nâng được kiện hàng 2 tấn lên cao 5 m trong 1 phút. Cần cẩu B nâng được kiện hàng 1,5 tấn lên cao 8 m trong 40 s. Xem lực nâng bằng với trọng lượng của kiện hàng. So sánh công suất của hai cần cẩu.
Phương pháp giải:
Vận dụng kiến thức đã học về các đại lượng:
- Công: \(A = F.s\)
- Công suất: \(P = \frac{A}{t}{\rm{ }}\)
Lời giải chi tiết:
Cần cẩu A thực hiện 1 công:
Aa = Fa.sa = 2000.10.5 = 105(J)
Công suất của cần cẩu A là:
Pa = Aa/ta = 105/60 = 1,67.103 (W)
Cần cẩu B thực hiện 1 công:
Ab = Fb.sb = 1500.10.8 = 12.104(J)
Công suất của cần cẩu B là:
Pb = Ab/tb = 12.104/40 = 3 000 (W)
Vậy, cần cẩu A có công suất nhỏ hơn cần cẩu B.
Câu hỏi tr 16 VD
Trả lời câu hỏi vận dụng trang 16 SGK KHTN 9 Chân trời sáng tạo
Trong mỗi nhịp đập, tìm người thực hiện một công xấp xỉ 1 J.
a) Tính công suất của tim, biết trung bình cứ một phút tim đập 72 lần.
b) Áp hai ngón tay vào vị trí động mạch trên cổ tay của em và đếm số lần tim đập trong một phút, từ đó tính công suất của tim.
Phương pháp giải:
Vận dụng kiến thức đã học về đại lượng công suất: \(P = \frac{A}{t}{\rm{ }}\)
Lời giải chi tiết:
a) Trong một phút, tim thực hiện được một công là: 1.72 = 72 (J)
Công suất của tim là: 72/60 = 1,2 (W)
b) Học sinh tự thực hiện và đếm
Luyện Bài Tập Trắc nghiệm KHTN 9 - Chân trời sáng tạo - Xem ngay
Các bài khác cùng chuyên mục
- Bài 23. Nguồn nhiên liệu trang 100, 101, 102 Khoa học tự nhiên 9 Chân trời sáng tạo
- Lý thuyết Năng lượng tái tạo - Khoa học tự nhiên 9 Chân trời sáng tạo
- Lý thuyết Năng lượng của Trái Đất. Năng lượng hóa thạch - Khoa học tự nhiên 9 Chân trời sáng tạo
- Lý thuyết Dòng điện xoay chiều - Khoa học tự nhiên 9 Chân trời sáng tạo
- Lý thuyết Cảm ứng điện từ - Khoa học tự nhiên 9 Chân trời sáng tạo
- Lý thuyết Năng lượng tái tạo - Khoa học tự nhiên 9 Chân trời sáng tạo
- Lý thuyết Năng lượng của Trái Đất. Năng lượng hóa thạch - Khoa học tự nhiên 9 Chân trời sáng tạo
- Lý thuyết Dòng điện xoay chiều - Khoa học tự nhiên 9 Chân trời sáng tạo
- Lý thuyết Cảm ứng điện từ - Khoa học tự nhiên 9 Chân trời sáng tạo
- Lý thuyết Năng lượng điện. Công suất điện - Khoa học tự nhiên 9 Chân trời sáng tạo











