 Toán 12 Cánh diều | Giải toán lớp 12 Cánh diều
Toán 12 Cánh diều | Giải toán lớp 12 Cánh diều
 Bài 2. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số ..
Bài 2. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số ..
Giải câu hỏi mở đầu trang 15 SGK Toán 12 tập 1 - Cánh diều
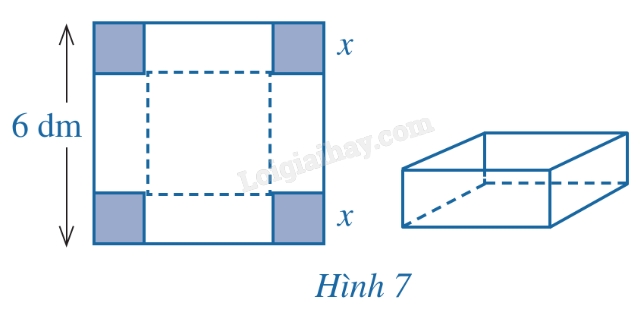
Cho một tấm nhôm có dạng hình vuông cạnh 6 dm. Bác Ánh cắt ở bốn góc bốn hình vuông có cùng độ dài cạnh bằng x (dm), rồi gập tấm nhôm lại như Hình 7 để được một cái hộp có dạng hình hộp chữ nhật không có nắp. Gọi V là thể tích của khối hộp đó.
GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT
Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn
Đề bài
Cho một tấm nhôm có dạng hình vuông cạnh 6 dm. Bác Ánh cắt ở bốn góc bốn hình vuông có cùng độ dài cạnh bằng x (dm), rồi gập tấm nhôm lại như Hình 7 để được một cái hộp có dạng hình hộp chữ nhật không có nắp. Gọi V là thể tích của khối hộp đó.
Phương pháp giải - Xem chi tiết
Lập hàm số biểu diễn thể tích hộp theo ẩn x. Tìm x để hàm số đạt giá trị lớn nhất.
Lời giải chi tiết
Thể tích của khối hộp là \(V(x) = x{\left( {6 - 2x} \right)^2}\) với 0 < x < 3.
Ta phải tìm \({x_0} \in (0;3)\) sao cho \(V\left( {{x_0}} \right)\) có giá trị lớn nhất.
Ta có: \(V'(x) = {(6 - 2x)^2} - 4x(6 - 2x)\)
\( = (6 - 2x)(6 - 6x) = 12(3 - x)(1 - x)\).
Trên khoảng (0;3), V’(x) = 0 khi x = 1.
Bảng biến thiên:
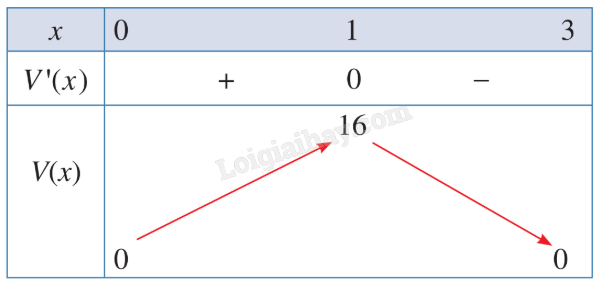
Dựa vào bảng biến thiên, ta thấy trên khoảng (0;3), hàm số V(x) đạt giá trị lớn nhất bằng 16 tại x = 1.
Vậy để khối hộp tạo thành có thể tích lớn nhất thì x = 1 (dm).
- Giải mục 1 trang 15, 16, 17 SGK Toán 12 tập 1 - Cánh diều
- Giải mục 2 trang 16, 17, 18 SGK Toán 12 tập 1 - Cánh diều
- Giải bài tập 1 trang 19 SGK Toán 12 tập 1 - Cánh diều
- Giải bài tập 2 trang 20 SGK Toán 12 tập 1 - Cánh diều
- Giải bài tập 3 trang 20 SGK Toán 12 tập 1 - Cánh diều
>> Xem thêm
Các bài khác cùng chuyên mục











