Giải bài tập 5 trang 103 SGK Toán 12 tập 2 - Cánh diều
Giả sử trong một nhóm người có 2 người nhiễm bệnh, 58 người còn lại là không nhiễm bệnh. Để phát hiện ra người nhiễm bệnh, người ta tiến hành xét nghiệm tất cả mọi người của nhóm đó. Biết rằng đối với người nhiễm bệnh thì xác suất xét nghiệm có kết quả dương tính là 85%, nhưng đối với người không nhiễm bệnh thì xác suất xét nghiệm có phản ứng dương tính là 7%. a) Vẽ sơ đồ hình cây biểu thị tình huống trên. b) Giả sử X là một người trong nhóm bị xét nghiệm có kết quả dương tính. Tính xác suất đ
Đề bài
Giả sử trong một nhóm người có 2 người nhiễm bệnh, 58 người còn lại là không nhiễm bệnh. Để phát hiện ra người nhiễm bệnh, người ta tiến hành xét nghiệm tất cả mọi người của nhóm đó. Biết rằng đối với người nhiễm bệnh thì xác suất xét nghiệm có kết quả dương tính là 85%, nhưng đối với người không nhiễm bệnh thì xác suất xét nghiệm có phản ứng dương tính là 7%.
a) Vẽ sơ đồ hình cây biểu thị tình huống trên.
b) Giả sử X là một người trong nhóm bị xét nghiệm có kết quả dương tính. Tính xác suất để X là người nhiễm bệnh.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về định nghĩa xác suất có điều kiện để tính: Cho hai biến cố A và B. Xác suất của biến cố A với điều kiện biến cố B đã xảy ra được gọi là xác suất của A với điều kiện B, kí hiệu là P(A|B). Nếu \(P\left( B \right) > 0\) thì \(P\left( {A|B} \right) = \frac{{P\left( {A \cap B} \right)}}{{P\left( B \right)}}\).
Sử dụng kiến thức về công thức xác suất toàn phần để tính: Cho hai biến cố A và B với \(0 < P\left( B \right) < 1\), ta có \(P\left( A \right) = P\left( {A \cap B} \right) + P\left( {A \cap \overline B } \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right)\).
Sử dụng kiến thức về sơ đồ hình cây để tính.
Lời giải chi tiết
a) Xét hai biến cố: A: “Người được chọn bị nhiễm bệnh”; B: “Người được chọn có phản ứng dương tính”.
Vì trong nhóm có 2 người nhiễm bệnh và 58 người còn lại không nhiễm bệnh nên \(P\left( A \right) = \frac{1}{{30}},P\left( {\overline A } \right) = \frac{{29}}{{30}}\).
Vì đối với người nhiễm bệnh thì xác suất xét nghiệm có kết quả dương tính là 85%, nhưng đối với người không nhiễm bệnh thì xác suất xét nghiệm có phản ứng dương tính là 7% nên \(P\left( {B|A} \right) = 0,85;P\left( {B|\overline A } \right) = 0,07\).
Sơ đồ cây biểu thị tình huống đã cho như sau:
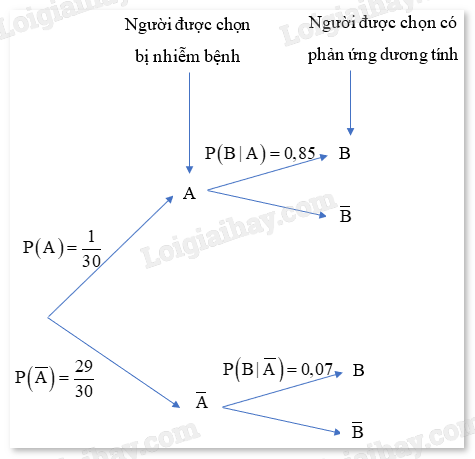
b) Ta có: \(P\left( {A|B} \right) = \frac{{P\left( A \right).P\left( {B|A} \right)}}{{P\left( B \right)}} = \frac{{P\left( A \right).P\left( {B|A} \right)}}{{P\left( A \right).P\left( {B|A} \right) + P\left( {\overline A } \right).P\left( {B|\overline A } \right)}}\)
\( = \frac{{\frac{1}{{30}}.0,85}}{{\frac{1}{{30}}.0,85 + \frac{{29}}{{30}}.0,07}} = \frac{{85}}{{288}} \approx 0,295\).
Vậy xác suất để X là người nhiễm bệnh là 0,295.
Các bài khác cùng chuyên mục











