Giải bài 9 trang 58 sách bài tập toán 9 - Cánh diều tập 2
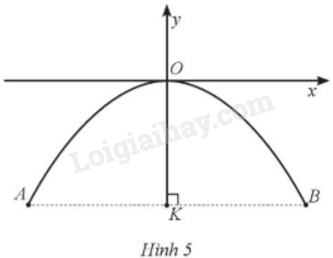
Một chiếc cổng hình parabol khi đưa vào hệ trục toạ độ Oxy có dạng một phần của parabol (y = - frac{1}{8}{x^2}), với gốc toạ độ O là vị trí cao nhất của cổng so với mặt đất, x và y được tính theo đơn vị mét, chiều cao OK của cổng là 4,5 m như mô tả ở Hình 5 (K là trung điểm của đoạn AB). Tìm khoảng cách giữa hai chân cổng A và B ở trên mặt đất.
Đề bài
Một chiếc cổng hình parabol khi đưa vào hệ trục toạ độ Oxy có dạng một phần của parabol \(y = - \frac{1}{8}{x^2}\), với gốc toạ độ O là vị trí cao nhất của cổng so với mặt đất, x và y được tính theo đơn vị mét, chiều cao OK của cổng là 4,5 m như mô tả ở Hình 5 (K là trung điểm của đoạn AB). Tìm khoảng cách giữa hai chân cổng A và B ở trên mặt đất.
Phương pháp giải - Xem chi tiết
Bước 1: Tìm tọa độ của K, từ đó tìm được tung độ của B.
Bước 2: Thay tọa độ B vào hàm số \(y = - \frac{1}{8}{x^2}\) (hoành độ của B là ẩn), từ đó tìm được hoành độ của B.
Bước 3: Tìm KB, AB.
Lời giải chi tiết
Vì \(OK = 4,5\)m và K nằm phía dưới trục Ox nên \(K\left( {0; - 4,5} \right)\).
Gọi hoành độ của B là b, tung độ của B bằng tung độ của K nên \(B\left( {b; - 4,5} \right)\).
Mặt khác, B thuộc đồ thị hàm số \(y = - \frac{1}{8}{x^2}\) nên ta có: \( - 4,5 = - \frac{1}{8}.{b^2}\)do đó \(b = 6\)
hay \(KB = 6m\).
Ta có \(AB = 2KB = 2.6 = 12\)m.
Vậy khoảng cách giữa hai chân cổng A và B ở trên mặt đất là 12m.
- Giải bài 10 trang 58 sách bài tập toán 9 - Cánh diều tập 2
- Giải bài 8 trang 58 sách bài tập toán 9 - Cánh diều tập 2
- Giải bài 7 trang 58 sách bài tập toán 9 - Cánh diều tập 2
- Giải bài 6 trang 58 sách bài tập toán 9 - Cánh diều tập 2
- Giải bài 5 trang 57 sách bài tập toán 9 - Cánh diều tập 2
>> Xem thêm
Các bài khác cùng chuyên mục













Danh sách bình luận