Giải bài 8 trang 58 sách bài tập toán 9 - Cánh diều tập 2

Nước từ một vòi nước (đặt trên mặt nước) được phun lên cao sẽ đạt đến một độ cao nào đó rồi rơi xuống (Hình 4). Giả sử nước được phun ra bắt đầu từ vị trí A trên mặt nước và rơi trở lại mặt nước ở vị trí B, đường đi của nước có dạng một phần của parabol (y = - frac{1}{4}{x^2}) trong hệ trục toạ độ Oxy, với gốc toạ độ O là vị trí cao nhất mà nước được phun ra đạt được so với mặt nước, trục Ox song song với AB, x và y được tính theo đơn vị mét. Tính chiều cao h từ điểm O đến mặt nước, biết kh

Đề bài

Nước từ một vòi nước (đặt trên mặt nước) được phun lên cao sẽ đạt đến một độ cao nào đó rồi rơi xuống (Hình 4). Giả sử nước được phun ra bắt đầu từ vị trí A trên mặt nước và rơi trở lại mặt nước ở vị trí B, đường đi của nước có dạng một phần của parabol \(y = - \frac{1}{4}{x^2}\) trong hệ trục toạ độ Oxy, với gốc toạ độ O là vị trí cao nhất mà nước được phun ra đạt được so với mặt nước, trục Ox song song với AB, x và y được tính theo đơn vị mét. Tính chiều cao h từ điểm O đến mặt nước, biết khoảng cách giữa điểm A và điểm B là 6 m.

Phương pháp giải - Xem chi tiết

Gọi I là trung điểm của AB.

Bước 1: Tính IA.

Bước 2: Thay tọa độ A hoặc B vào hàm số \(y = - \frac{1}{4}{x^2}\) để tìm h.

Lời giải chi tiết

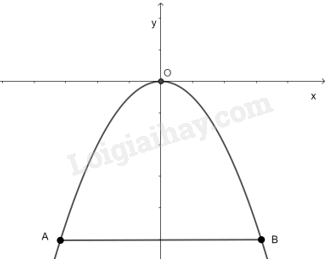
Gọi I là trung điểm của AB, ta có OI là khoảng cách từ O đến AB hay từ O đến mặt nước. Vậy \(h = OI\).

Vì I là trung điểm của AB nên \(AI = BI = \frac{{AB}}{2} = \frac{6}{2} = 3\)cm.

Trong hệ trục tọa độ Oxy có; hoành độ của B là 3, tung độ là \( - h\), và B thuộc đồ thị hàm số \(y = - \frac{1}{4}{x^2}\) nên \( - h = - \frac{1}{4}{.3^2}\), do đó \(h = \frac{9}{4} = 2,25\)m.

Vậy chiều cao h từ điểm O đến mặt nước là 2,25m.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 9 trang 58 sách bài tập toán 9 - Cánh diều tập 2
Một chiếc cổng hình parabol khi đưa vào hệ trục toạ độ Oxy có dạng một phần của parabol (y = - frac{1}{8}{x^2}), với gốc toạ độ O là vị trí cao nhất của cổng so với mặt đất, x và y được tính theo đơn vị mét, chiều cao OK của cổng là 4,5 m như mô tả ở Hình 5 (K là trung điểm của đoạn AB). Tìm khoảng cách giữa hai chân cổng A và B ở trên mặt đất.
Giải bài 10 trang 58 sách bài tập toán 9 - Cánh diều tập 2
a) Vẽ đồ thị các hàm số (y = - frac{3}{2}{x^2})và (y = frac{3}{2}{x^2})trên cùng một mặt phẳng toạ độ Oxy. b) Qua đồ thị của các hàm số đó, hãy cho biết khi x tăng từ 0,5 đến 2 thì giá trị lớn nhất của hàm số (y = - frac{3}{2}{x^2}) và giá trị nhỏ nhất của hàm số (y = frac{3}{2}{x^2}) là bao nhiêu?
Giải bài 7 trang 58 sách bài tập toán 9 - Cánh diều tập 2
Cho hàm số (y = k{x^2}left( {k ne 0} right)) có đồ thị là một parabol với đỉnh O như Hình 3. a) Tìm giá trị của k. b) Tìm tung độ của điểm thuộc parabol có hoành độ bằng 2. c) Tìm các điểm thuộc parabol có tung độ bằng 2. d*) Tìm các điểm (không phải điểm O) thuộc parabol sao cho khoảng cách từ điểm đó đến trục hoành gấp ba lần khoảng cách từ điểm đó đến trục tung.
Giải bài 6 trang 58 sách bài tập toán 9 - Cánh diều tập 2
Cho A là giao điểm của hai đường thẳng (y = x - 1) và (y = - 2x + 8). Chứng minh rằng điểm A thuộc đồ thị hàm số (y = frac{2}{9}{x^2}).
Giải bài 5 trang 57 sách bài tập toán 9 - Cánh diều tập 2
a) Điểm (Aleft( {0,2;1} right)) thuộc đồ thị hàm số nào trong các hàm số sau: (y = 10{x^2};y = - 10{x^2};y = 25{x^2};y = - 25{x^2};y = frac{1}{{25}}{x^2};y = - frac{1}{{25}}{x^2}) b) Trong các điểm (Bleft( { - 2;4sqrt 3 } right);Cleft( { - 2; - 4sqrt 3 } right);Dleft( { - 0,2; - 0,4sqrt 3 } right);Eleft( {0,4sqrt 3 ;0,2} right)), điểm nào thuộc đồ thị hàm số (y = - sqrt 3 {x^2}).
Giải bài 4 trang 57 sách bài tập toán 9 - Cánh diều tập 2
Một viên bi lăn trên mặt phẳng nghiêng. Đoạn đường đi được liên hệ với thời gian bởi hàm số (y = a{t^2}) (t tính bằng giây, y tính bằng mét). Người ta đo được quãng đường viên bi lăn được ở thời điểm 3 giây là 2,25 m. Hỏi khi viên bi lăn được quãng đường 6,25 m thì nó đã lăn trong bao lâu?
Giải bài 3 trang 57 sách bài tập toán 9 - Cánh diều tập 2
Galileo Galilei là người phát hiện ra quãng đường chuyển động của vật rơi tự do tỉ lệ thuận với bình phương của thời gian. Liên hệ giữa quãng đường chuyển động s (mét) và thời gian chuyển động x (giây) được cho bởi hàm số (s = 4,9{x^2}). Người ta thả một vật nặng từ độ cao 56 m trên tháp nghiêng Pi-sa xuống đất (sức cản của không khí không đáng kể). a) Hỏi sau thời gian 2,5 giây vật nặng còn cách mặt đất bao nhiêu mét? b) Khi vật nặng còn cách mặt đất 17,584 m thì nó đã rơi thời gian bao nhi
Giải bài 2 trang 57 sách bài tập toán 9 - Cánh diều tập 2
Cho hàm số (y = - a{x^2}(a ne 0)) (a ≠ 0). Tìm a, biết khi (x = 1,2) thì (y = - 2,88).
Giải bài 1 trang 57 sách bài tập toán 9 - Cánh diều tập 2
Diện tích toàn phần của hình lập phương cạnh a được cho bởi công thức (S = 6{a^2}). a) Tính các giá trị của S rồi hoàn thiện bảng sau: b) Tính cạnh a của hình lập phương (theo đơn vị centimét và làm tròn kết quả đến hàng phần trăm), biết diện tích toàn phần của hình lập phương đó bằng 42 cm2.