Giải bài 8 trang 98 sách bài tập toán 9 - Chân trời sáng tạo tập 1

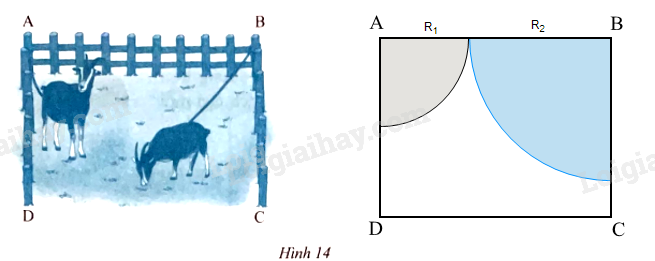
Một vườn cỏ có dạng hình chữ nhật ABCD với AB = 40 m, AD = 30 m. Người ta muốn buộc hai con dê ở hai góc vườn A, B. Có hai cách buộc: Cách 1: Mỗi dây thừng dài 20 m. Cách 2: Một dây thừng dài 30 m và một dây thừng dài 10 m. Hỏi với cách buộc nào thì diện tích cỏ mà hai con dê có thể ăn được sẽ lớn hơn?

Tổng hợp đề thi học kì 1 lớp 9 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - KHTN - Lịch sử và Địa lí

Đề bài

Một vườn cỏ có dạng hình chữ nhật ABCD với AB = 40 m, AD = 30 m. Người ta muốn buộc hai con dê ở hai góc vườn A, B. Có hai cách buộc:

Cách 1: Mỗi dây thừng dài 20 m.

Cách 2: Một dây thừng dài 30 m và một dây thừng dài 10 m.

Hỏi với cách buộc nào thì diện tích cỏ mà hai con dê có thể ăn được sẽ lớn hơn?

Phương pháp giải - Xem chi tiết

Dựa vào: Diện tích hình quạt tròn: \(S = \frac{{\pi {R^2}n}}{{360}}\).

Lời giải chi tiết

Diện tích cỏ hai con dê có thể ăn là dạng hai hình quạt có số đo cung cùng bằng 90^o.

TH1: Mỗi dây thừng dài 20 m suy ra R₁ = R₂ = 20 m.

Diện tích cỏ mà hai con dê có thể ăn:

\(S = {S_1} + {S_2} = \frac{{\pi R_1^2.90}}{{360}} + \frac{{\pi R_2^2.90}}{{360}} \\= \frac{{\pi {{.20}^2}.90}}{{360}} + \frac{{\pi {{.20}^2}.90}}{{360}} = 200\pi ({m^2})\)

TH2: Giả sử dây thừng cột con dê ở A dài 30 m, dây thừng cột con dê ở B dài 10 m.

Suy ra R₁ = 30 m, R₂ = 10 m.

Diện tích cỏ mà hai con dê có thể ăn:

\(S = {S_1} + {S_2} = \frac{{\pi R_1^2.90}}{{360}} + \frac{{\pi R_2^2.90}}{{360}} \\= \frac{{\pi {{.30}^2}.90}}{{360}} + \frac{{\pi {{.10}^2}.90}}{{360}} = 250\pi ({m^2}).\)

Vậy dùng hai sợi dây 30 m và 10 m thì diện tích cỏ hai con dê sẽ ăn nhiều hơn.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 3 trang 97 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Một biểu đồ hình quạt tròn được vẽ trong đường tròn bán kính R = 15 cm (Hình 10). Tính diện tích của mỗi hình quạt tròn trong biểu đồ đó.
Giải bài 7 trang 97 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Một chiếc bàn hình tròn được ghép bởi hai nửa hình tròn đường kính AB = 1,2 m. Người ta muốn nới rộng mặt bàn bằng cách ghép thêm vào giữa một mặt hình chữ nhật có một kích thước là 1,2 m. a) Kích thước còn lại của hình chữ nhật phải là bao nhiêu nếu diện tích mặt bàn tăng gấp đôi sau khi nới? b) Kích thước còn lại của hình chữ nhật phải là bao nhiêu nếu chu vi mặt bàn tăng gấp đôi sau khi nới?
Giải bài 6 trang 97 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Một ống thép có đường kính ngoài là 100 mm và đường kính trong là 80 mm. Tính diện tích mặt cắt ngang của ống thép đó.
Giải bài 5 trang 97 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Hai trạm phát sóng A và B đặt cách nhau 100 km. Trạm phát sóng A và trạm phát sóng B có bán kính hoạt động lần lượt là 50 km và (50sqrt 3 ) km. Tính diện tích của khu vực có thể đặt thiết bị thu sóng sao cho thu được cả hai sóng phát từ trạm A và trạm B. Biết rằng nếu khoảng cách từ thiết bị thu sóng đến trạm phát sóng lớn hơn bán kính hoạt động của trạm phát sóng thì thiết bị không thu được sóng của trạm phát sóng đó.
Giải bài 4 trang 97 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Tính diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; 8 cm) và (O; 24 cm).
Giải bài 2 trang 97 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Cho đường tròn (O) đường kính AB = 3 cm, (widehat {CAB}) = 30o (Hình 9). a) Tính độ dài cung BmD. b) Tính diện tích hình quạt tròn OBmD.
Giải bài 1 trang 96 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Quan sát Hình 8 và tính a) Số đo cung AmB. b) Độ dài cung AmB. c) Diện tích hình quạt tròn OAmB. d) Diện tích hình viên phân giới hạn bởi cung AmB và dây AB.