-
Toán 8 tập 1 - Cánh diều
-
Toán 8 tập 2 - Cánh diều
-
Chương 6 Một số yếu tố thống kê và xác suất
- Bài 1. Thu thập và phân loại dữ liệu
- Bài 2. Mô tả và biểu diễn dữ liệu trên các bảng, biểu đồ
- Bài 3. Phân tích và xử lí dữ liệu thu được ở dạng bảng, biểu đồ
- Bài 4. Xác suất của biến cố ngẫu nhiên trong một số trò chơi đơn giản
- Bài 5. Xác suất thực nghiệm của một biến cố trong một số trò chơi đơn giản
- Bài tập cuối chương 6
-
Chương 7 Phương trình bậc nhất một ẩn
-
Chương 8 Tam giác đồng dạng. Hình đồng dạng
- Bài 1. Định lí Thalès trong tam giác
- Bài 2. Ứng dụng của định lí Thalès trong tam giác
- Bài 3. Đường trung bình của tam giác
- Bài 4. Tính chất đường phân giác của tam giác
- Bài 5. Tam giác đồng dạng
- Bài 6. Trường hợp đồng dạng thứ nhất của tam giác
- Bài 7. Trường hợp đồng dạng thứ hai của tam giác
- Bài 8. Trường hợp đồng dạng thứ ba của tam giác
- Bài 9. Hình đồng dạng
- Bài 10. Hình đồng dạng trong thực tiễn
- Bài tập cuối chương 8
-
Giải bài 8 trang 95 SGK Toán 8 – Cánh diều
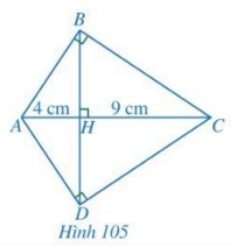
Cho Hình 105. Chứng minh:
Tổng hợp đề thi học kì 2 lớp 8 tất cả các môn - Cánh diều
Toán - Văn - Anh - Khoa học tự nhiên
Đề bài
Cho Hình 105. Chứng minh:
a) \(\Delta HAB \backsim \Delta HBC\)
b) \(HB = HD = 6cm\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Chứng minh \(\widehat {HBC} = \widehat {BAH}\) rồi chứng minh hai tam giác đồng dạng.
b) Tính độ dài HB và HD rồi so sánh với nhau.
Lời giải chi tiết
a) Xét tam giác ABC vuông tại B có: \(\widehat {BAC} + \widehat {BCA} = 90^\circ \)
Xét tam giác BHC vuông tại H có:
\(\begin{array}{l}\widehat {HBC} + \widehat {HCB} = 90^\circ \\ \Rightarrow \widehat {HBC} + \widehat {BCA} = 90^\circ \end{array}\)
\( \Rightarrow \widehat {HBC} = \widehat {BAC}\) hay \(\widehat {HBC} = \widehat {BAH}\)
Xét tam giác HAB và tam giác HBC có:
\(\widehat {BAH} = \widehat {CBH}\) và \(\widehat {BHA} = \widehat {CHB} = 90^\circ \)
\( \Rightarrow \Delta HAB \backsim \Delta HBC\)
b) Vì \(\Delta HAB \backsim \Delta HBC\) nên
\(\begin{array}{l}\frac{{HA}}{{HB}} = \frac{{HB}}{{HC}}\\ \Rightarrow H{B^2} = HA.HC\\ \Rightarrow H{B^2} = 4.9 = 36\\ \Rightarrow HB = 6cm\end{array}\)
Ta chứng minh được \(\Delta HAD \backsim \Delta HDC\)
\(\begin{array}{l} \Rightarrow \frac{{HA}}{{HD}} = \frac{{HD}}{{HC}}\\ \Rightarrow H{D^2} = HA.HC\\ \Rightarrow H{D^2} = 4.9 = 36\\ \Rightarrow HD = 6cm\end{array}\)
Vậy \(HB = HD = 6cm\).
Bình luận
Chia sẻ
- Giải bài 9 trang 95 SGK Toán 8 – Cánh diều
- Giải bài 10 trang 96 SGK Toán 8 – Cánh diều
- Giải bài 11 trang 96 SGK Toán 8 – Cánh diều
- Giải bài 12 trang 96 SGK Toán 8 – Cánh diều
- Giải bài 13 trang 96 SGK Toán 8 – Cánh diều
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Cánh diều - Xem ngay
Tham Gia Group Dành Cho 2K10 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến lớp 9 & lộ trình Up 10! trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3 bước: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục
