Toán 8, giải toán lớp 8 cánh diều Bài tập cuối chương 8 Toán 8 cánh diều

Giải bài 4 trang 94 SGK Toán 8 – Cánh diều


Cho tứ giác ABCD. Tia phân giác của các góc BAD và BCD cắt nhau tại điểm I

Tổng hợp đề thi học kì 2 lớp 8 tất cả các môn - Cánh diều

Toán - Văn - Anh - Khoa học tự nhiên

Đề bài

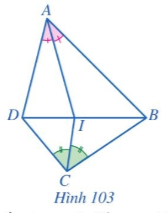
Cho tứ giác ABCD. Tia phân giác của các góc BAD và BCD cắt nhau tại điểm I. Biết I thuộc đoạn thẳng BD (Hình 103). Chứng minh \(AB.CD = AD.BC\).

 

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Dựa vào tính chất đường phân giác để suy ra các tỉ lệ tương ứng.

Lời giải chi tiết

Vì AI là đường phân giác của góc DAB nên \(\frac{{ID}}{{IB}} = \frac{{AD}}{{AB}}\) (Tính chất đường phân giác)

Vì CI là đường phân giác của góc BCD nên \(\frac{{ID}}{{IB}} = \frac{{CD}}{{CB}}\) (Tính chất đường phân giác)

\( \Rightarrow \frac{{AD}}{{AB}} = \frac{{CD}}{{CB}} \Rightarrow AB.CD = AD.BC\)


Bình chọn:
3.7 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 8 - Cánh diều - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K10 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

>> Học trực tuyến lớp 9 & lộ trình Up 10! trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3 bước: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua