 Giải vth Toán 7, soạn vở thực hành Toán 7 KNTT
Giải vth Toán 7, soạn vở thực hành Toán 7 KNTT
 Bài 28. Phép chia đa thức một biến trang 45, 46, 47, 48..
Bài 28. Phép chia đa thức một biến trang 45, 46, 47, 48..
Giải bài 8 trang 49 vở thực hành Toán 7 tập 2
Cho đa thức (P = 6{x^3} + 5{x^2} + 4x + m) và (Q = 2{x^2} + x + 1). Tìm số m để phép chia P: Q là một phép chia hết.
Đề bài
Cho đa thức \(P = 6{x^3} + 5{x^2} + 4x + m\) và \(Q = 2{x^2} + x + 1\). Tìm số m để phép chia P: Q là một phép chia hết.
Phương pháp giải - Xem chi tiết
Khi chia đa thức A cho đa thức B ta được đa thức thương là Q, đa thức dư là R thì nếu \(R = 0\) thì ta có phép chia hết.
Lời giải chi tiết
Trước hết ta tìm dư trong phép chia P cho Q bằng cách đặt tính chia:
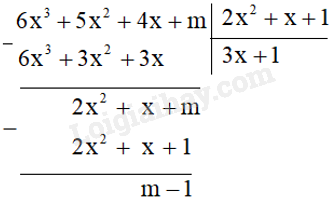
Vậy \(\left( {6{x^3} + 5{x^2} + 4x + m} \right):\left( {2{x^2} + x + 1} \right) = 3x + 1\) (dư \(m - 1\)).
Muốn có phép chia hết, ta phải có dư là 0, tức là \(m - 1 = 0\), suy ra \(m = 1\).
- Giải bài 7 trang 48, 49 vở thực hành Toán 7 tập 2
- Giải bài 6 (7.35) trang 48 vở thực hành Toán 7 tập 2
- Giải bài 5 (7.34) trang 47, 48 vở thực hành Toán 7 tập 2
- Giải bài 4 (7.33) trang 47 vở thực hành Toán 7 tập 2
- Giải bài 3 (7.32) trang 47 vở thực hành Toán 7 tập 2
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 7 - Kết nối tri thức - Xem ngay
Các bài khác cùng chuyên mục












Danh sách bình luận