SBT Toán 12 - giải SBT Toán 12 - Cánh diều Bài 3. Đường tiệm cận của đồ thị hàm số - SBT Toán 12 C..

Giải bài 67 trang 26 sách bài tập toán 12 - Cánh diều


Tổng chi phí để sản xuất (x) sản phẩm của một xí nghiệp được tính theo công thức (T = 20x + 100{rm{ }}000) (nghìn đồng). a) Viết công thức tính chi phí trung bình (Cleft( x right)) của 1 sản phẩm khi sản xuất được (x) sản phẩm. b) Xem (y = Cleft( x right)) là một hàm số xác định trên khoảng (left( {0; + infty } right)), hãy tìm tiệm cận ngang của đồ thị hàm số đó. c) Xét tính đơn điệu của hàm số (y = Cleft( x right)) trên khoảng (left( {0; + infty } right)).

Đề bài

Tổng chi phí để sản xuất \(x\) sản phẩm của một xí nghiệp được tính theo công thức

\(T = 20x + 100{\rm{ }}000\) (nghìn đồng).

a) Viết công thức tính chi phí trung bình \(C\left( x \right)\) của 1 sản phẩm khi sản xuất được \(x\) sản phẩm.

b) Xem \(y = C\left( x \right)\) là một hàm số xác định trên khoảng \(\left( {0; + \infty } \right)\), hãy tìm tiệm cận ngang của đồ thị hàm số đó.

c) Xét tính đơn điệu của hàm số \(y = C\left( x \right)\) trên khoảng \(\left( {0; + \infty } \right)\).

d) Nêu nhận xét về chi phí để tạo ra 1 sản phẩm khi \(x\) càng lớn.

Phương pháp giải - Xem chi tiết

Tìm tiệm cận ngang: Nếu \(\mathop {\lim }\limits_{x \to  + \infty } f\left( x \right) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to  - \infty } f\left( x \right) = {y_0}\) thì đường thẳng \(y = {y_0}\) là đường tiệm cận ngang.

Lời giải chi tiết

a) Công thức tính chi phí trung bình \(C\left( x \right)\) của 1 sản phẩm khi sản xuất được \(x\) sản phẩm là: \(C\left( x \right) = \frac{{20x + 100000}}{x}\).

b) Ta có:

\(\mathop {\lim }\limits_{x \to  + \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to  + \infty } \frac{{20x + 100000}}{x} = 20\)

Vậy \(y = 20\) là tiệm cận ngang của đồ thị hàm số đã cho.

c) Ta có:

\({y^\prime } = \frac{{ - 100000}}{{{x^2}}} < 0,\forall x \in \left( {0; + \infty } \right)\)

Bảng biến thiên của hàm số:

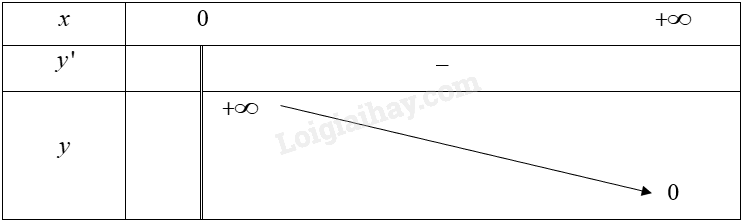
Vậy hàm số nghịch biến trên khoảng \(\left( {0; + \infty } \right)\).

d) Do đường thẳng \(y = 20\) là tiệm cận ngang của đồ thị hàm số \(y = C\left( x \right)\) nên khi \(x\) càng lớn thì chi phí để tạo ra 1 sản phẩm sẽ giảm gần đến mức 20 nghìn đồng và không thể giảm hơn 20 nghìn đồng cho dù số sản phẩm sản xuất được có thể lớn vô cùng.


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo
  • Giải bài 66 trang 26 sách bài tập toán 12 - Cánh diều

    Tốc độ đánh máy trung bình (S) (tính bằng từ trên phút) của một học viên sau (t) tuần học được cho bởi công thức: (Sleft( t right) = frac{{100{t^2}}}{{65 + {t^2}}}) với (t > 0). a) Xem (y = Sleft( t right) = frac{{100{t^2}}}{{65 + {t^2}}}) là một hàm số xác định trên khoảng (left( {0; + infty } right)), hãy tìm tiệm cận ngang của đồ thị hàm số đó. b) Nêu nhận xét về tốc độ đánh máy trung bình của học viên đó khi thời gian (t) càng lớn.

  • Giải bài 65 trang 26 sách bài tập toán 12 - Cánh diều

    Tìm tiệm cận đứng, tiệm cận ngang, tiệm cận xiên (nếu có) của đồ thị mỗi hàm số sau: a) (y = frac{{3{rm{x}} + 5}}{{{x^2} - 4}}); b) (y = frac{{ - {x^2} - 1}}{{4{{rm{x}}^2} + 9}}); c) (y = frac{{3{x^2} + x}}{{1 - x}}).

  • Giải bài 64 trang 26 sách bài tập toán 12 - Cánh diều

    Tìm tiệm cận đứng, tiệm cận xiên của đồ thị mỗi hàm số sau: a) (y = 5{rm{x}} - 2 + frac{1}{{x + 3}}); b) (y = - 7{rm{x}} + frac{{x - 1}}{{{x^2}}}); c) (y = frac{{{x^2} + 2{rm{x}}}}{{ - x + 2}}); d) (y = frac{{2{{rm{x}}^2} + 9{rm{x}}}}{{x + 1}});

  • Giải bài 63 trang 26 sách bài tập toán 12 - Cánh diều

    Tìm tiệm cận đứng, tiệm cận ngang của đồ thị mỗi hàm số sau: a) (y = frac{{x - 1}}{{2{rm{x}} + 3}}); b) (y = - 3 + frac{5}{{x - 4}}); c) (y = frac{{3{rm{x}} - 7}}{{{x^2}}}); d) (y = frac{{ - 2{{rm{x}}^2} + 1}}{{{x^2} - 2{rm{x}} + 1}}).

  • Giải bài 62 trang 26 sách bài tập toán 12 - Cánh diều

    Trong mỗi ý a), b), c), d), chọn phương án đúng (Đ) hoặc sai (S). Cho hàm số (y = frac{{{x^2} - 3}}{{ - x - 1}}). a) Đồ thị hàm số có tiệm cận đứng là đường thẳng (x = - 1). b) Đồ thị hàm số có tiệm cận ngang là đường thẳng (y = - 1). c) Đồ thị hàm số có tiệm cận xiên là đường thẳng (y = - x). d) Giao điểm (I) của hai đường tiệm cận của đồ thị hàm số là (Ileft( { - 1;1} right)).

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 12 - Cánh diều - Xem ngay

Báo lỗi - Góp ý

Group Ôn Thi ĐGNL & ĐGTD Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store