Giải bài 6 trang 66 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Kết quả kiểm tra tình trạng cân nặng của các học sinh lớp 9B được thống kê lại ở bảng sau: Chọn ngẫu nhiên 1 học sinh lớp 9B. Tính xác suất của mỗi biến cố sau: A: “Học sinh được chọn là học sinh nữ và có cân nặng bình thường”; B: “Học sinh được chọn bị thừa cân”; C: “Học sinh được chọn là học sinh nam”.
Tổng hợp đề thi học kì 1 lớp 9 tất cả các môn - Chân trời sáng tạo
Toán - Văn - Anh - KHTN - Lịch sử và Địa lí
Đề bài
Kết quả kiểm tra tình trạng cân nặng của các học sinh lớp 9B được thống kê lại ở bảng sau:
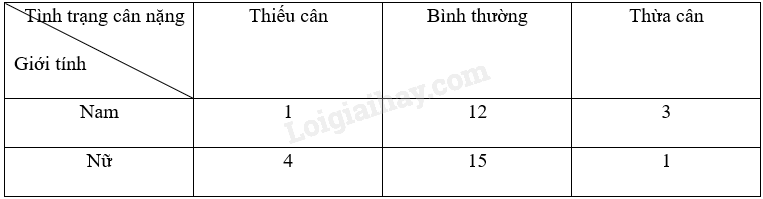
Chọn ngẫu nhiên 1 học sinh lớp 9B. Tính xác suất của mỗi biến cố sau:
A: “Học sinh được chọn là học sinh nữ và có cân nặng bình thường”;
B: “Học sinh được chọn bị thừa cân”;
C: “Học sinh được chọn là học sinh nam”.
Phương pháp giải - Xem chi tiết
Trong phép thử ngẫu nhiên, hai kết quả đồng khả năng nếu chúng có khả năng xảy ra như nhau.
Xác suất của biến cố A được tính bởi công thức:
\(P(A) = \frac{{n(A)}}{{n(\Omega )}}\), trong đó n(A) là số kết quả thuận lợi cho A; \(n(\Omega )\) là số các kết quả có thể xảy ra.
Lời giải chi tiết
Tổng số học sinh là 1 + 12 + 3 + 4 + 15 + 1 = 36 (học sinh).
Số các kết quả có thể xảy ra là \(n(\Omega ) = 36\).
Số học sinh nữ có cân nặng bình thường là 15 nên số kết quả thuận lợi cho biến cố A là n(A) = 15.
Xác suất của biến cố A là P(A) = \(\frac{{15}}{{36}} = \frac{5}{{12}}\).
Số học sinh bị thừa cân là 3 + 1 = 4 (học sinh).
Số kết quả thuận lợi cho biến cố B là n(B) = 4
Xác suất của biến cố B là \(P(B) = \frac{4}{{36}} = \frac{1}{9}\).
Số học sinh nam 1 + 12 + 3 = 16 (học sinh).
Số kết quả thuận lợi cho biến cố C là n(C) = 16.
Xác suất của biến cố C là P(C) = \(\frac{{16}}{{36}} = \frac{4}{9}\).
- Giải bài 7 trang 66 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 8 trang 67 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 3 trang 66 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 5 trang 66 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 4 trang 66 sách bài tập toán 9 - Chân trời sáng tạo tập 2
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Chân trời sáng tạo - Xem ngay
Các bài khác cùng chuyên mục
- Giải bài 4 trang 86 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 1 trang 98 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 16 trang 109 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 15 trang 109 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 14 trang 109 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 16 trang 109 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 15 trang 109 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 14 trang 109 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 13 trang 109 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 12 trang 108 sách bài tập toán 9 - Chân trời sáng tạo tập 2












