Giải bài 6 trang 55 sách bài tập toán 12 - Chân trời sáng tạo

Cho hình chóp (S.ABCD) có đáy (ABCD) là hình vuông cạnh bằng 4. Mặt bên (SAB) là tam giác cân tại (S) có chiều cao bằng 6 và nằm trong mặt phẳng vuông góc với đáy. a) Tính góc (alpha ) giữa hai đường thẳng (SD) và (BC); b) Tính góc (beta ) giữa hai mặt phẳng (left( {SAD} right)) và (left( {SCD} right)).

Đề bài

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh bằng 4. Mặt bên \(SAB\) là tam giác cân tại \(S\) có chiều cao bằng 6 và nằm trong mặt phẳng vuông góc với đáy.

a) Tính góc \(\alpha \) giữa hai đường thẳng \(SD\) và \(BC\);

b) Tính góc \(\beta \) giữa hai mặt phẳng \(\left( {SAD} \right)\) và \(\left( {SCD} \right)\).

Phương pháp giải - Xem chi tiết

Gắn vào hệ trục toạ độ và sử dụng công thức góc giữa hai đường thẳng và góc giữa hai mặt phẳng.

Lời giải chi tiết

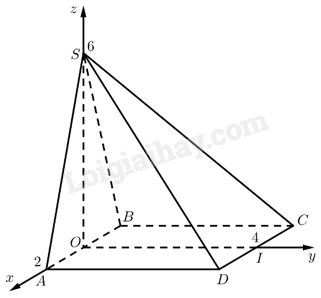
Gọi \(O\) là trung điểm của \(AB\), \(I\) là trung điểm của \(C{\rm{D}}\).

\(SAB\) là tam giác cân tại \(S\) nên \(SO \bot AB\), suy ra \(SO \bot \left( {ABCD} \right)\).

Chọn hệ trục \(Oxyz\) như hình vẽ. Ta có:

\(S\left( {0;0;6} \right),A\left( {2;0;0} \right),B\left( { - 2;0;0} \right),C\left( { - 2;4;0} \right),D\left( {2;4;0} \right)\).

a) Ta có \(\overrightarrow {SD} = \left( {2;4; - 6} \right),\overrightarrow {BC} = \left( {0;4;0} \right)\), suy ra

\(\cos \left( {S{\rm{D}},BC} \right) = \left| {\cos \left( {\overrightarrow {S{\rm{D}}} ,\overrightarrow {BC} } \right)} \right| = \frac{{\left| {2.0 + 4.4 + \left( { - 6} \right).0} \right|}}{{\sqrt {{2^2} + {4^2} + {{\left( { - 6} \right)}^2}} .\sqrt {{0^2} + {4^2} + {0^2}} }} = \frac{{\sqrt {14} }}{7}\)

Vậy \(\left( {S{\rm{D}},BC} \right) \approx {57,7^ \circ }\).

b) Ta có: \(\overrightarrow {SD} = \left( {2;4; - 6} \right),\overrightarrow {SA} = \left( {2;0; - 6} \right) \Rightarrow \left[ {\overrightarrow {SD} ,\overrightarrow {SA} } \right] = \left( { - 24;0; - 8} \right) = - 8\left( {3;0;1} \right)\).

Do đó \(\left( {SAD} \right)\) có vectơ pháp tuyến \(\overrightarrow n = \left( {3;0;1} \right)\).

\(\overrightarrow {SD} = \left( {2;4; - 6} \right),\overrightarrow {CD} = \left( {4;0;0} \right) \Rightarrow \left[ {\overrightarrow {SD} ,\overrightarrow {CD} } \right] = \left( {0; - 24; - 16} \right) = - 8\left( {0;3;2} \right)\).

Do đó \(\left( {SCD} \right)\) có vectơ pháp tuyến \(\overrightarrow {n'} = \left( {0;3;2} \right)\).

\(\cos \left( {\left( {SAD} \right),\left( {SCD} \right)} \right) = \left| {\cos \left( {\overrightarrow n ,\overrightarrow {n'} } \right)} \right| = \frac{{\left| {3.0 + 0.3 + 1.2} \right|}}{{\sqrt {{3^2} + {0^2} + {1^2}} .\sqrt {{0^2} + {3^2} + {2^2}} }} = \frac{{2\sqrt {130} }}{{130}}\)

Vậy \(\left( {\left( {SAD} \right),\left( {SCD} \right)} \right) \approx {79,9^ \circ }\).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 7 trang 55 sách bài tập toán 12 - Chân trời sáng tạo
Người ta muốn dựng một cột ăng-ten trên một sườn đồi. Ăng-ten được dựng thẳng đứng trong không gian \(Oxyz\) với độ dài đơn vị trên mỗi trục bằng 1 m. Gọi \(O\) là gốc cột, \(A\) là điểm buộc dây cáp vào cột ăng-ten và \(M,N\) là hai điểm neo dây cáp xuống mặt sườn đồi (Hình 6). Cho biết toạ độ các điểm nói trên lần lượt là \(O\left( {0;0;0} \right),A\left( {0;0;6} \right),M\left( {3; - 4;3} \right),\)\(N\left( { - 5; - 2;2} \right)\). a) Tính độ dài các đoạn dây cáp \(MA\) và \(NA\). b) Tính
Giải bài 5 trang 55 sách bài tập toán 12 - Chân trời sáng tạo
Tính góc \(\alpha \) trong mỗi trường hợp sau: a) \(\alpha \) là góc giữa hai vectơ \(\overrightarrow a = \left( {1;1; - 1} \right)\) và \(\overrightarrow b = \left( {5;2;7} \right)\); b) \(\alpha \) là góc giữa hai đường thẳng \(d:\left\{ \begin{array}{l}x = 1 + t\\y = 2 - \sqrt 3 t\\z = 5\end{array} \right.\) và \(d':\left\{ \begin{array}{l}x = 1 - \sqrt 3 t'\\y = 7 + t'\\z = 9\end{array} \right.\). c) \(\alpha \) là góc giữa hai mặt phẳng \(\left( P \right):4x + 2y - z + 9 = 0\) và \(\
Giải bài 4 trang 54 sách bài tập toán 12 - Chân trời sáng tạo
Xác định vị trí tương đối của hai đường thẳng (d) và (d') trong mỗi trường hợp sau: a) (d:left{ begin{array}{l}x = t\y = 1 + 3t\z = 1 - tend{array} right.) và (d':left{ begin{array}{l}x = 2 + 2t'\y = 7 + 6t'\z = - 1 - 2t'end{array} right.); b) (d:frac{{x - 2}}{2} = frac{y}{3} = frac{z}{1}) và (d':frac{x}{4} = frac{y}{6} = frac{z}{2}); c) (d:left{ begin{array}{l}x = 1 + t\y = 1 + t\z = 2 - tend{array} right.) và (d':frac{{x - 2}}{2} = frac{{y - 2}}{
Giải bài 3 trang 54 sách bài tập toán 12 - Chân trời sáng tạo
Lập phương trình chính tắc của đường thẳng (d) trong mỗi trường hợp sau: a) (d) đi qua điểm (Mleft( {9;0;0} right)) và có vectơ chỉ phương (overrightarrow a = left( {5; - 11;4} right)); b) (d) đi qua hai điểm (Aleft( {6;0; - 1} right),Bleft( {8;3;2} right)); c) (d) có phương trình tham số (left{ begin{array}{l}x = 2t\y = - 1 + 7t\z = 3 - 6tend{array} right.).
Giải bài 2 trang 54 sách bài tập toán 12 - Chân trời sáng tạo
Lập phương trình tham số của đường thẳng (d) trong mỗi trường hợp sau: a) (d) đi qua điểm (Aleft( {1; - 5;0} right)) và có vectơ chỉ phương (overrightarrow a = left( {2;0;7} right)); b) (d) đi qua hai điểm (Mleft( {3; - 1; - 1} right),Nleft( {5;1;2} right)).
Giải bài 1 trang 54 sách bài tập toán 12 - Chân trời sáng tạo
Cho đường thẳng (d) có phương trình tham số (left{ begin{array}{l}x = 7 + 5t\y = 3 + 11t\z = 9 - 6tend{array} right.). Tìm một điểm trên (d) và một vectơ chỉ phương của (d).