Giải bài 6 trang 46 sách bài tập toán 12 - Chân trời sáng tạo

Cho hình hộp chữ nhật (ABCD.A'B'C'D') có (DA = 2,DC = 3,DD = 2). Tính khoảng cách từ đỉnh (B') đến mặt phẳng (left( {BA'C'} right)).

Đề bài

Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(DA = 2,DC = 3,DD = 2\).

Tính khoảng cách từ đỉnh \(B'\) đến mặt phẳng \(\left( {BA'C'} \right)\).

Phương pháp giải - Xem chi tiết

Gắn vào hệ trục toạ độ và sử dụng công thức tính khoảng cách từ một điểm đến một mặt phẳng.

Lời giải chi tiết

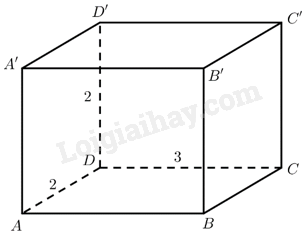
Vì \(ABCD.A'B'C'D'\) là hình hộp chữ nhật nên các đường thẳng \(DA,DC,DD'\) đôi một vuông góc.

Do đó ta có thể gắn hệ trục toạ độ \(Oxyz\) thoả mãn \(D\left( {0;0;0} \right),A\left( {2;0;0} \right),C\left( {0;3;0} \right),D'\left( {0;0;2} \right)\).

Khi đó \(B\left( {2;3;0} \right),B'\left( {2;3;2} \right),A'\left( {2;0;2} \right),C'\left( {0;3;2} \right)\).

Ta có: \(\overrightarrow {BA'} = \left( {0; - 3;2} \right),\overrightarrow {BC'} = \left( { - 2;0;2} \right)\).

Khi đó, \(\left[ {\overrightarrow {BA'} ,\overrightarrow {BC'} } \right] = \left( {\left( { - 3} \right).2 - 2.0;2.\left( { - 2} \right) - 0.2;0.0 - \left( { - 3} \right).\left( { - 2} \right)} \right) = \left( { - 6; - 4; - 6} \right)\) là vectơ pháp tuyến của mặt phẳng \(\left( {BA'C'} \right)\).

Phương trình mặt phẳng \(\left( {BA'C'} \right)\) là:

\( - 6\left( {x - 2} \right) - 4\left( {y - 3} \right) - 6\left( {z - 0} \right) = 0 \Leftrightarrow - 6x - 4y - 6{\rm{z}} + 24 = 0 \Leftrightarrow 3{\rm{x}} + 2y + 3{\rm{z}} - 12 = 0\).

Khi đó khoảng cách từ điểm \(B'\) đến mặt phẳng \(\left( {BA'C'} \right)\) bằng:

\(d\left( {B',\left( {BA'C'} \right)} \right) = \frac{{\left| {3.2 + 2.3 + 3.2 - 12} \right|}}{{\sqrt {{3^2} + {2^2} + {3^2}} }} = \frac{{3\sqrt {22} }}{{11}}\).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 7 trang 46 sách bài tập toán 12 - Chân trời sáng tạo
Một kĩ sư xây dựng thiết kế khung một ngôi nhà trong không gian (Oxyz) như Hình 9 nhờ một phần mềm đồ hoạ máy tính. a) Viết phương trình mặt phẳng mái nhà (left( {DEMM} right)). b) Tính khoảng cách từ điểm (B) đến mái nhà (left( {DEMM} right)).
Giải bài 5 trang 46 sách bài tập toán 12 - Chân trời sáng tạo
Cho hai mặt phẳng \(\left( P \right):2x + y + 2z + 12 = 0,\left( Q \right):4x + 2y + 4z - 6 = 0\). a) Chứng minh \(\left( P \right)\parallel \left( Q \right)\). b) Tính khoảng cách giữa hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\).
Giải bài 4 trang 45 sách bài tập toán 12 - Chân trời sáng tạo
Tính khoảng cách từ điểm (Aleft( {1;2;3} right)) đến các mặt phẳng sau: a) (left( P right):3x + 4z + 10 = 0); b) (left( Q right):2x - 10 = 0); c) (left( R right):2x + 2y + z - 3 = 0).
Giải bài 3 trang 45 sách bài tập toán 12 - Chân trời sáng tạo
Tìm các cặp mặt phẳng song song hoặc vuông góc trong các mặt phẳng sau: \(\left( P \right):x + y - z + 3 = 0,\left( Q \right):2x + 2y - 2z + 99 = 0,\left( R \right):3x + 3y + 6z + 7 = 0\).
Giải bài 2 trang 45 sách bài tập toán 12 - Chân trời sáng tạo
Lập phương trình mặt phẳng \(\left( P \right)\) trong mỗi trường hợp sau: a) \(\left( P \right)\) đi qua điểm \(M\left( {1;2;3} \right)\) và có vectơ pháp tuyến \(\overrightarrow n = \left( {3;1; - 2} \right)\); b) \(\left( P \right)\) đi qua điểm \(N\left( { - 2;3;0} \right)\) và có cặp vectơ chỉ phương \(\overrightarrow u = \left( {1;1;1} \right),\overrightarrow v = \left( {3;0;4} \right)\). c) \(\left( P \right)\) đi qua ba điểm \(A\left( {1;2;2} \right),B\left( {5;3;2} \right),C\lef
Giải bài 1 trang 45 sách bài tập toán 12 - Chân trời sáng tạo
Cho mặt phẳng (left( Q right)) nhận (overrightarrow a = left( {4;0;1} right);overrightarrow b = left( {2;1;1} right)) làm cặp vectơ chỉ phương. Tìm một vectơ pháp tuyến của (left( Q right)).