Toán 8, giải toán lớp 8 cánh diều Bài 5. Tam giác đồng dạng Toán 8 cánh diều

Giải bài 5 trang 73 SGK Toán 8 – Cánh diều


Cho tam giác ABC (Hình 55), các điểm M, N thuộc cạnh AB thỏa mãn

Tổng hợp đề thi học kì 2 lớp 8 tất cả các môn - Cánh diều

Toán - Văn - Anh - Khoa học tự nhiên

Đề bài

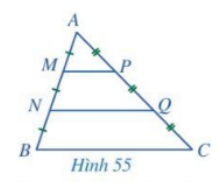
Cho tam giác ABC (Hình 55), các điểm M, N thuộc cạnh AB thỏa mãn \(AM = MN = NB\), các điểm P, Q thuộc cạnh AC thỏa mãn \(AP = PQ = QC\). Tam giác AMP đồng dạng với những tam giác nào?

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Sử dụng định lý về cặp tam giác đồng dạng nhận được từ định lý Thales để tìm ra các cặp tam giác đồng dạng.

Lời giải chi tiết

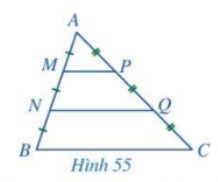
Vì \(AM = MN = NB\) và \(AP = PQ = QC\) nên M và P lần lượt là trung điểm của AN và AQ.

Khi đó MP là đường trung bình của tam giác ANQ.

\(\Rightarrow MP//NQ\)

\(\Rightarrow \Delta AMP \backsim \Delta ANQ\) (theo định lí)

\(\Rightarrow \widehat {AMP} = \widehat {ANQ}\)

Ta có:

\(\frac{{AM}}{{AB}} = \frac{{AP}}{{AC}} = \frac{1}{3} \Rightarrow MP//BC\) (Định lý Thales đảo)

\( \Rightarrow \Delta AMP \backsim \Delta ABC\).


Bình chọn:
3.7 trên 6 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 8 - Cánh diều - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K10 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

>> Học trực tuyến lớp 9 & lộ trình Up 10! trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3 bước: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua