Giải bài 5 trang 11 sách bài tập toán 9 - Chân trời sáng tạo tập 1

Cho hai đường thẳng (y = - frac{1}{2}x - 3) và y = -3x + 2. Vẽ hai đường thẳng đó trên cùng một hệ trục toạ độ. Xác định toạ độ giao điểm A của hai đường thẳng và cho biết toạ độ của điểm A có là nghệm của hệ phương trình (left{ {begin{array}{*{20}{c}}{x + 2y = - 6}{3x + y = 2}end{array}} right.) không. Tại sao?

Tổng hợp đề thi học kì 1 lớp 9 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - KHTN - Lịch sử và Địa lí

Đề bài

Cho hai đường thẳng \(y = - \frac{1}{2}x - 3\) và y = -3x + 2. Vẽ hai đường thẳng đó trên cùng một hệ trục toạ độ. Xác định toạ độ giao điểm A của hai đường thẳng và cho biết toạ độ của điểm A có là nghệm của hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{x + 2y = - 6}\\{3x + y = 2}\end{array}} \right.\) không. Tại sao?

Phương pháp giải - Xem chi tiết

Xét phương trình hoành độ giao điểm để tìm giao điểm A và thay vào hệ phương trình để kiểm tra.

Vẽ hai đường thẳng trên trục toạ độ.

Lời giải chi tiết

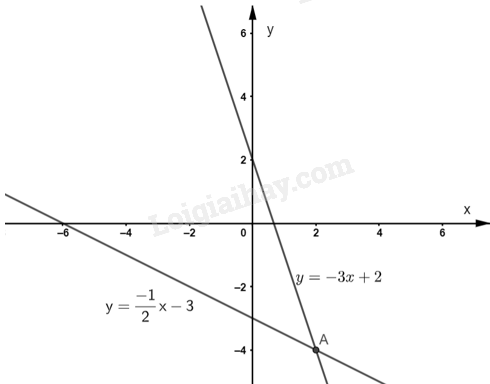
Toạ độ giao điểm A của hai đường thẳng là A(2;-4).

Viết lại \(y = - \frac{1}{2}x - 3\) thành x + 2y = -6 và y = - 3x + 2 thành 3x + y = 2.

Vậy toạ độ giao điểm A(2; - 4) là nghiệm của hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{x + 2y = - 6}\\{3x + y = 2}\end{array}} \right.\).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 4 trang 11 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Cho ba phương trình x + 2y = -1; 2x – y = 7; - x + 3y = -9 Hãy lập một hệ hai phương trình bậc nhất hai ẩn từ ba phương trình đã cho sao cho hệ cặp số (3; - 2) làm nghiệm.
Giải bài 3 trang 10 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Biểu diễn tất cả các nghiệm của mỗi phương trình sau trên mặt phẳng toạ độ Oxy. a) 2x + y = - 2 b) 0x – y = -3 c) – 4x + 0y = 6
Giải bài 2 trang 10 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Cho hệ phương trình (left{ {begin{array}{*{20}{c}}{3x + 2y = 7}\{ - x - 4y = - 9}end{array}} right.) Trong các cặp số (3;2), (1;2), (5;1), cặp số nào là nghiệm của hệ phương trình đã cho?
Giải bài 1 trang 10 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Trong các cặp số (1;1), (-2;-4), (-2;6), (left( {3; - frac{1}{4}} right)), cặp số nào là nghiệm của mỗi phương trình sau? a) 5x + 3y = 8 b) 3x – 4y = 10