Bài 3. Đường trung bình của tam giác Toán 8 cánh diều

Giải bài 2 trang 65 SGK Toán 8 – Cánh diều

Cho tam giác ABC có AM là đường trung tuyến, các điểm N, P phân biệt thuộc cạnh AB

Đề bài

Cho tam giác ABC có AM là đường trung tuyến, các điểm N, P phân biệt thuộc cạnh AB sao cho \(AP = PN = NB\). Gọi Q là giao điểm của AM và CP. Chừng minh:

a) \(MN//CP\)

b) \(AQ = QM\)

c) \(CP = 4PQ\)

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

a) Chứng minh MN là đường trung bình của tam giác BPC.

b) Sử dụng định lý Thales trong tam giác AMN để chứng minh.

c) Sử dụng định lý đường trung bình để chứng minh.

Lời giải chi tiết

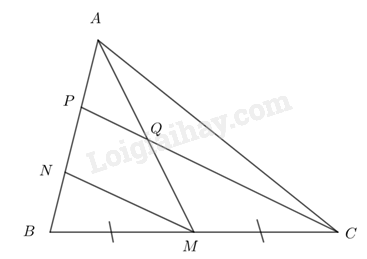
a) Vì \(AP = PN = NB\) nên N là trung điểm BP.

Mà M là trung điểm BC nên MN là đường trung bình của tam giác BPC.

\( \Rightarrow MN//CP\)

b) Tam giác AMN có \(MN//CP\) nên:

\(\frac{{AP}}{{PN}} = \frac{{AQ}}{{QM}}\) (Định lý Thales)

Mà \(AP = PN = NB\) nên P là trung điểm AN hay \(\frac{{AP}}{{PN}} = 1\)

\( \Rightarrow \frac{{AQ}}{{QM}} = 1 \Rightarrow AQ = QM\).

c) P là trung điểm AN, Q là trung điểm AM nên PQ là đường trung bình của tam giác AMN.

\( \Rightarrow PQ = \frac{1}{2}MN\)

Mà MN là đường trung bình của tam giác BPC nên \(MN = \frac{1}{2}CP \Rightarrow CP = 2MN\)

Vậy \(CP = 4PQ\).

Bình luận

Chia sẻ

Bình chọn:

4.2 trên 6 phiếu

Bài tiếp theo

Giải bài 3 trang 65 SGK Toán 8 – Cánh diều
Cho tứ giác ABCD có M, N, P, Q lần lượt là trung điểm của các cạnh
Giải bài 4 trang 65 SGK Toán 8 – Cánh diều
Cho tam giác ABC nhọn có H là trực tâm. Gọi M, N, P, Q lần lượt là trung điểm của các đoạn thẳng
Giải bài 5 trang 65 SGK Toán 8 – Cánh diều
Trong Hình 36, ba cạnh màu vàng AB, BC, CA gợi nên hình ảnh tam giác ABC
Giải bài 1 trang 65 SGK Toán 8 – Cánh diều
Cho tam giác ABC có M là trung điểm của AB, điểm N thuộc cạnh AC thỏa mãn
Giải mục 2 trang 63, 64 SGK Toán 8 – Cánh diều
Cho tam giác ABC có MN là đường trung bình (Hình 31).
Giải mục 1 trang 62 SGK Toán 8 – Cánh diều
Quan sát ta, giác ABC ở Hình 29 và cho biết hai đầu mút D, E của đoạn thẳng
Lý thuyết Đường trung bình của tam giác SGK Toán 8 - Cánh diều
Đường trung bình trong tam giác là gì?