Giải Bài 2 trang 65 sách bài tập toán 7 - Chân trời sáng tạo

Cho tam giác ABC có \(\widehat {{A^{}}} = {42^o}\), ba đường phân giác đồng quy tại I. Tính số đo góc BIC.

Toán - Văn - Anh - KHTN...

Đề bài

Cho tam giác ABC có \(\widehat {{A^{}}} = {42^o}\), ba đường phân giác đồng quy tại I. Tính số đo góc BIC.

Phương pháp giải - Xem chi tiết

Sử dụng tính chất tia phân giác của một góc để tính số đo góc.

Lời giải chi tiết

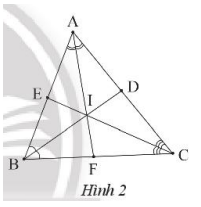
Ta có: \(\widehat B + \widehat C = {180^o} - \widehat {{A^{}}} = {180^o} - {62^o} = {118^o}\)

Do BI và CI là phân giác của góc B và góc C của tam giác ABC nên:

\(\widehat {IBC} + \widehat {ICB} = \frac{{\widehat B + \widehat C}}{2} = \frac{{{{118}^o}}}{2} = {59^o}\)

Suy ra: \(\widehat {BIC} = {180^o} - \left( {\widehat {IBC} + \widehat {ICB}} \right) = {180^o} - {59^o} = {121^o}\)

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Giải Bài 3 trang 65 sách bài tập toán 7 - Chân trời sáng tạo
Cho tam giác ABC cân tại A. Vẽ đường phân giác AD. Gọi H và K là chân các đường vuông góc kẻ từ D đến AB và AC. Chứng minh rằng DH = DK.
Giải Bài 4 trang 65 sách bài tập toán 7 - Chân trời sáng tạo
Cho tam giác ABC có đường trung tuyến AM đồng thời là đường phân giác. Chứng minh tam giác ABC là tam giác cân.
Giải Bài 1 trang 65 sách bài tập toán 7 - Chân trời sáng tạo
Cho tam giác ABC cân tại A. Gọi G là trọng tâm của tam giác và gọi I là giao điểm của các đường phân giác của tam giác. Chứng minh ba điểm A, I, G thẳng hàng.