 Giải chuyên đề học tập Toán lớp 11 Chân trời sáng tạo
Giải chuyên đề học tập Toán lớp 11 Chân trời sáng tạo
 Bài 2. Phép tịnh tiến Chuyên đề học tập Toán 11 Chân tr..
Bài 2. Phép tịnh tiến Chuyên đề học tập Toán 11 Chân tr..
Giải bài 2 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Cho đường tròn (O) và hai điểm A, B. Khi điểm M thay đổi trên đường tròn (O) thì điểm M’ thay đổi trên đường nào để \(\overrightarrow {MM'} + \overrightarrow {MA} = \overrightarrow {MB} \)?
Đề bài
Cho đường tròn (O) và hai điểm A, B. Khi điểm M thay đổi trên đường tròn (O) thì điểm M’ thay đổi trên đường nào để \(\overrightarrow {MM'} + \overrightarrow {MA} = \overrightarrow {MB} \)?
Phương pháp giải - Xem chi tiết
Vẽ hình và sử dụng quy tắc hình bình hành để làm
Lời giải chi tiết
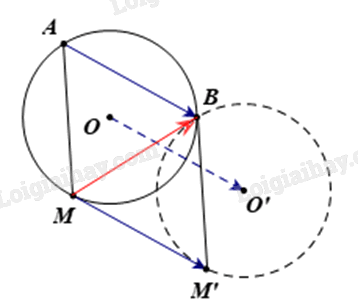
Do A, B cố định nên \(\overrightarrow {AB} \) là vectơ không đổi.
Từ dữ kiện \(\overrightarrow {MM'} + \overrightarrow {MA} = \overrightarrow {MB} \), áp dụng quy tắc hình bình hành, ta có tứ giác ABM’M là hình bình hành.
Do đó \(\overrightarrow {MM'} = \overrightarrow {AB} \)
Vì vậy M’ là ảnh của M qua phép tịnh tiến \({T_{\overrightarrow {AB} }}\).
Vậy khi M thay đổi trên đường tròn (O) thì M’ nằm trên ảnh của đường tròn (O) là đường tròn (O’) qua phép tịnh tiến \({T_{\overrightarrow {AB} }}\).
- Giải bài 3 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải bài 4 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải bài 5 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải bài 1 trang 14 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải mục 2 trang 12, 13 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Chân trời sáng tạo - Xem ngay
Các bài khác cùng chuyên mục
- Giải mục 2 trang 84, 85 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
- Giải bài 3 trang 29 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải bài 11 trang 92 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải bài 12 trang 92 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải bài 10 trang 92 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải mục 2 trang 84, 85 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
- Giải bài 3 trang 29 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải bài 12 trang 92 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải bài 11 trang 92 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải bài 10 trang 92 Chuyên đề học tập Toán 11 Chân trời sáng tạo











