-
GIẢI TÍCH SBT - TOÁN 12
-
HÌNH HỌC SBT - TOÁN 12
Bài 1.70 trang 38 SBT giải tích 12
Giải bài 1.70 trang 38 sách bài tập giải tích 12. Biểu thức tổng quát của hàm số có đồ thị như hình 1.6 là:...
Đề bài
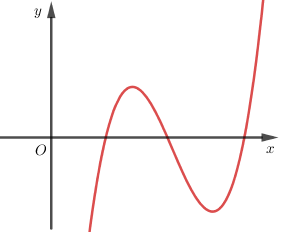
Biểu thức tổng quát của hàm số có đồ thị như hình \(1.6\) là:
A. \(y = a{x^2} + bx + c\) với \(a \ne 0\).
B. \(y = a{x^3} + cx + d\) với \(a < 0\).
C. \(y = a{x^3} + b{x^2} + cx + d\) với \(a > 0\) và \({b^2} - 3ac > 0\).
D. \(y = {x^3}\).
Phương pháp giải - Xem chi tiết
- Nhận xét dáng đồ thị, số điểm cực trị và loại đáp án.
Lời giải chi tiết
Quan sát dáng đồ thị ta thấy:
+ Đây là đồ thị hàm đa thức bậc ba. Loại A.
+ Có \(\mathop {\lim }\limits_{x \to + \infty } y = + \infty ,\mathop {\lim }\limits_{x \to - \infty } y = - \infty \) nên hệ số \(a > 0\). Loại B.
+ Đáp án D có \(y' = 3{x^2} \ge 0,\forall x\) nên hàm số đồng biến trên \(\mathbb{R}\) và không có cực trị nên loại D.
Chọn C.
Chú ý:
Đáp án C có \(y' = 3a{x^2} + 2bx + c\) và \(\Delta ' = {b^2} - 3ac > 0\) nên phương trình \(y' = 0\) có hai nghiệm phân biệt hay đồ thị hàm số có hai điểm cực trị.
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 1.71 trang 39 SBT giải tích 12
- Bài 1.72 trang 39 SBT giải tích 12
- Bài 1.73 trang 39 SBT giải tích 12
- Bài 1.74 trang 39 SBT giải tích 12
- Bài 1.69 trang 38 SBT giải tích 12
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
