Giải bài 1.41 trang 31 sách bài tập toán 12 - Kết nối tri thức

Bác Hưng có một hàng rào thép dài (240) m và muốn rào cánh đồng thành một thửa ruộng hình chữ nhật giáp một con sông thẳng. Bác không cần rào phía cạnh con sông. Hỏi thửa ruộng có thể tích lớn nhất là bao nhiêu?

Đề bài

Bác Hưng có một hàng rào thép dài \(240\) m và muốn rào cánh đồng thành một thửa ruộng hình chữ nhật giáp một con sông thẳng. Bác không cần rào phía cạnh con sông. Hỏi thửa ruộng có diện tích lớn nhất là bao nhiêu?

Phương pháp giải - Xem chi tiết

+ Đặt độ dài các cạnh của thửa ruộng là các biến \(x,{\rm{ y}}\).

+ Biểu diễn y theo x, từ đó thu được công thức diện tích của thửa ruộng là \(S\left( x \right)\).

+ Tìm giá trị lớn nhất của \(S\left( x \right)\).

Lời giải chi tiết

Gọi độ dài hai cạnh của thửa ruộng hình chữ nhật lần lượt là \(x,{\rm{ y}}\) (m), \(\left( {x,{\rm{ y > }}0} \right)\).

Giả sử cạnh \(y\) giáp với con sông.

Do hàng rào thép dài \(240\) m nên ta có \(2x + y = 240\). Suy ra \(x \le 120\).

Diện tích của thửa ruộng là \(S = xy = x\left( {240 - 2x} \right) = 240x - 2{x^2}\)

Ta có \(S' = 240 - 4x\) khi đó \(S' = 0 \Leftrightarrow 240 - 4x = 0 \Leftrightarrow x = 60\) suy ra \(y = 240 - 2 \cdot 60 = 120\).

Lập bảng biến thiên

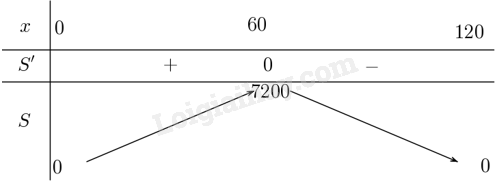
Từ bảng biến thiên suy ra giá trị lớn nhất của hàm số là \(S\left( {60} \right) = 60 \cdot 120 = 7200\).

Vậy thửa ruộng có diện tích lớn nhất là \(7200\) m² (khi cạnh giáp sông và cạnh đối diện nó có độ dài \(120\) m, độ dài hai cạnh còn lại là \(60\)m.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 1.42 trang 31 sách bài tập toán 12 - Kết nối tri thức
Doanh số bán hệ thống âm thanh nổi mới trong khoảng thời gian dự kiến sẽ tuân theo đường cong logistic \(R = R\left( x \right) = \frac{{5000}}{{1 + 5{e^{ - x}}}},x \ge 0\), trong đó thời gian \(x\) được tính bằng năm. Hỏi tốc độ bán hàng đạt tối đa vào năm nào?
Giải bài 1.43 trang 31 sách bài tập toán 12 - Kết nối tri thức
Một chiếc hộp dạng hình hộp chữ nhật có đáy là hình vuông và có thể tích là \(2000\) cm3. Các kích thước của chiếc hộp là bao nhiêu nếu muốn lượng vật liệu dùng để sản xuất chiếc hộp là nhỏ nhất?
Giải bài 1.44 trang 31 sách bài tập toán 12 - Kết nối tri thức
Một hòn đảo nhỏ cách điểm P trên bờ biển khoảng (3) km, một thị trấn ở điểm A cách điểm P (12) km (xem hình vẽ). Nếu một người trên đảo chèo thuyền với vận tốc (2,5) km/h và đi bộ với vận tốc (4) km/h thì thuyền nên neo đậu ở vị trí nào trên đoạn PA để người đó đến thị trấn trong thời gian ngắn nhất?
Giải bài 1.45 trang 32 sách bài tập toán 12 - Kết nối tri thức
Chứng tỏ rẳng một thùng hình trụ có thể tích (V) cố định cần ít vật liệu sản xuất nhất (tức là có diện tích bề mặt nhỏ nhất) khi chiều cao của thùng gấp đôi bán kính đáy.
Giải bài 1.46 trang 32 sách bài tập toán 12 - Kết nối tri thức
Ở ({0^ circ }C), sự mất nhiệt (H) (tính bằng Kcal/m2h, ở đây Kcal là kilocalories và 1 Kcal=1000 calo) từ cơ thể của một người có thể được mô hình hóa bằng công thức (H = 33left( {10sqrt v - v + 10,45} right),) Trong đó (v) là tốc độ gió (tính bằng m/s) (Theo sách Brief Calculus: An Applied Approach, 8th edition, Cengage Learning, 2009). a) Xét tính đơn điệu của hàm số (H) và giải thích ý nghĩa thực tiễn của kết quả nhận được. b) Tìm tốc độ thay đổi của (H) khi (v = 2) m/
Giải bài 1.47 trang 32 sách bài tập toán 12 - Kết nối tri thức
Doanh thu (R) (USD) từ vệc cho thuê (x) căn hộ có thể được mô hình hóa bằng hàm số (R = 2xleft( {900 + 32x - {x^2}} right)). a) Tìm hàm doanh thu biên. b) Tìm doanh thu biên khi (x = 14) và giải thích ý nghĩa thực tiễn của nó. c) Tìm lượng doanh thu tăng thêm khi số căn hộ cho thuê tăng từ (14) lên (15).
Giải bài 1.48 trang 32 sách bài tập toán 12 - Kết nối tri thức
Một công ty ước tính rằng chi phí (C) (USD) để sản xuất (x) đơn vị sản phẩm có thể được mô hình hóa bằng công thức (C = 800 + 0,04x + 0,0002{x^2}). Tìm mức sản xuất sao cho chi phí trung bình (overline C left( x right) = frac{{Cleft( x right)}}{x}) cho mỗi đơn vị hàng hóa là nhỏ nhất.
Giải bài 1.49 trang 32 sách bài tập toán 12 - Kết nối tri thức
a) Nếu \(C\left( x \right)\) (USD) là chi phí sản xuất \(x\) đơn vị hàng hóa, thì chi phí trung bình cho mỗi đơn vị là \(\overline C \left( x \right) = \frac{{C\left( x \right)}}{x}\). Chứng minh rằng nếu chi phí trung bình là nhỏ nhất thì chi phí biên bằng chi phí trung bình. b) Nếu \(C\left( x \right) = 16000 + 200x + 4{x^{\frac{3}{2}}}\), hãy tìm: (i) Chi phí, chi phí trung bình và chi phí biên khi sản xuất \(100\) đơn vị hàng hóa; (ii) Mức sản xuất mà khi đó sẽ giảm thiểu chi phí trung bì
Giải bài 1.50 trang 33 sách bài tập toán 12 - Kết nối tri thức
a) Chứng tỏ rằng nếu lợi nhuận (Pleft( x right)) là cực đại thì doanh thu biên bằng chi phí biên. b) Cho (Cleft( x right) = 16000 + 500x - 1,6{x^2} + 0,004{x^3}) là hàm chi phí và (pleft( x right) = 1700 - 7x) là hàm cầu. Hãy tìm mức sản xuất sẽ tối đa lợi nhuận.