Đề số 28 - Đề thi vào lớp 10 môn Toán

Đề bài

Câu 1 (2 điểm):

Giải phương trình và hệ phương trình:

$1)\;\;\dfrac{{3x + 1}}{2} - x = 1$   

$2)\;\;\left\{ \begin{array}{l}3x = 17 - y\\x - 2y = 1\end{array} \right.$

Câu 2 (2 điểm):

1) Tìm $m$ để phương trình ${d_1}:\;y = \left( {{m^2} + 1} \right)x + 2m - 3$ cắt đường thẳng $d:\;y = x - 3$ tại điểm $A$ có hoành độ bằng $- 1.$

2) Rút gọn biểu thức $A = \left( {\dfrac{1}{{x + \sqrt x }} - \dfrac{1}{{\sqrt x  + 1}}} \right):\dfrac{{\sqrt x  - 1}}{{x + 2\sqrt x  + 1}} + 1$ với $x > 0,\;\;x \ne 1.$

Câu 3 (2 điểm):

1) Quãng đường Hải Dương – Hạ Long dài 100km. Một ô tô đi từ Hải Dương đến Hạ Long rồi nghỉ ở đó 8 giờ 20 phút, sau đó trở về Hải Dương hết tất cả 12 giờ. Tính vận tốc của ô tô lúc đi, biết vận tốc ô tô lúc về nhanh hơn vận  tốc ô tô lúc đi 10 km/h.

2) Tìm $m$ để phương trình ${x^2} - 2mx + {m^2} - 2 = 0$ (x là ẩn, m là tham số) có hai nghiệm phân biệt ${x_1},\;{x_2}$ thỏa mãn $\left| {x_1^3 - x_2^3} \right| = 10\sqrt 2 .$

Câu 4 (3 điểm):

Cho tam giác ABC nội tiếp đường tròn tâm O đường kính BC. Kẻ AH vuông góc với BC (H thuộc BC), gọi M, N lần lượt là hình chiếu vuông góc của H trên AB và AC.

1) Chứng minh $A{C^2} = CH.CB.$

2) Chứng minh tứ giác $BCNM$ nội tiếp và $AC.BM + AB.CN = AH.BC.$

3) Đường thẳng đi qua A cắt tia HM tại E và cắt tia đối của tia NH tại F. Chứng minh BE // CF.

Câu 5 (1 điểm):

Cho phương trình $a{x^2} + bx + c = 0\;\;\left( {a \ne 0} \right)$ có hai nghiệm ${x_1},\;{x_2}$ thỏa mãn $0 \le {x_1} \le {x_2} \le 2.$ Tìm giá trị nhỏ nhất của biểu thức $L = \dfrac{{3{a^2} - ab + ac}}{{5{a^2} - 3ab + {b^2}}}.$

Lời giải chi tiết

Câu 1:

$\begin{array}{l}1)\;\;\dfrac{{3x + 1}}{2} - x = 1\\ \Leftrightarrow 3x + 1 - 2x = 2\\ \Leftrightarrow x = 1.\end{array}$

Vậy phương trình có nghiệm duy nhất: $x = 1.$

$\begin{array}{l}2)\;\;\left\{ \begin{array}{l}3x = 17 - y\\x - 2y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x + y = 17\\x - 2y = 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}3x + y = 17\\3x - 6y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}7y = 14\\x = 2y + 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}y = 2\\x = 2.2. + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 5\\y = 2\end{array} \right..\end{array}$

Vậy hệ phương trình có nghiệm duy nhất $\left( {x;\;y} \right) = \left( {5;\;2} \right).$

Câu 2:

1) Tìm $m$ để phương trình ${d_1}:\;y = \left( {{m^2} + 1} \right)x + 2m - 3$ cắt đường thẳng $d:\;y = x - 3$ tại điểm $A$ có hoành độ bằng $- 1.$

Phương trình hoành độ giao điểm của hai đường thẳng đã cho là:

$\left( {{m^2} + 1} \right)x + 2m - 3 = x - 3 \Leftrightarrow {m^2}x + 2m = 0.\;\;\;\;\left( * \right)$

Hai đường thẳng cắt nhau tại điểm $A$ có hoành độ bằng $- 1$ thì $x =  - 1$ là nghiệm của phương trình (*). Khi đó:

$\begin{array}{l}\left( * \right) \Leftrightarrow  - {m^2} + 2m = 0\\ \Leftrightarrow m\left( {m - 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m = 0\\m - 2 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}m = 0\\m = 2\end{array} \right..\end{array}$

Vậy $m = 0$ hoặc $m = 2.$

2) Rút gọn biểu thức $A = \left( {\dfrac{1}{{x + \sqrt x }} - \dfrac{1}{{\sqrt x  + 1}}} \right):\dfrac{{\sqrt x  - 1}}{{x + 2\sqrt x  + 1}} + 1$ với $x > 0,\;\;x \ne 1.$

Điều kiện: $x > 0,\;\;x \ne 1.$

$\begin{array}{l}A = \left( {\dfrac{1}{{x + \sqrt x }} - \dfrac{1}{{\sqrt x  + 1}}} \right):\dfrac{{\sqrt x  - 1}}{{x + 2\sqrt x  + 1}} + 1\\\;\;\; = \left( {\dfrac{1}{{\sqrt x \left( {\sqrt x  + 1} \right)}} - \dfrac{1}{{\sqrt x  + 1}}} \right):\dfrac{{\sqrt x  - 1}}{{{{\left( {\sqrt x  + 1} \right)}^2}}} + 1\\\;\;\; = \dfrac{{1 - \sqrt x }}{{\sqrt x \left( {\sqrt x  + 1} \right)}}.\dfrac{{{{\left( {\sqrt x  + 1} \right)}^2}}}{{\sqrt x  - 1}} + 1\\\;\;\; =  - \dfrac{{\sqrt x  + 1}}{{\sqrt x }} + 1\\\;\;\; = \dfrac{{ - \sqrt x  - 1 + \sqrt x }}{{\sqrt x }} =  - \dfrac{1}{{\sqrt x }}.\end{array}$

Câu 3:

1) Quãng đường Hải Dương – Hạ Long dài 100km. Một ô tô đi từ Hải Dương đến Hạ Long rồi nghỉ ở đó 8 giờ 20 phút, sau đó trở về Hải Dương hết tất cả 12 giờ. Tính vận tốc của ô tô lúc đi, biết vận tốc ô tô lúc về nhanh hơn vận  tốc ô tô lúc đi 10 km/h.

Gọi vận tốc của ô tô lúc đi là $x\;\left( {km/h} \right),\;\;\left( {x > 0} \right).$

Khi đó vận tốc lúc về của ô tô là: $x + 10\;\;\left( {km/h} \right).$

Thời gian ô tô đi từ Hải Dương đến Hạ Long là: $\dfrac{{100}}{x}\;\;\left( h \right).$

Thời gian ô tô đi từ Hạ Long về Hải Dương là: $\dfrac{{100}}{{x + 10}}\;\;\left( h \right).$

Đổi $8$ giờ $20$ phút $= \dfrac{{25}}{3}$ giờ.

Theo đề bài ta có phương trình:

$\begin{array}{l}\;\;\;\;\dfrac{{100}}{x} + \dfrac{{25}}{3} + \dfrac{{100}}{{x + 10}} = 12\\ \Leftrightarrow \dfrac{{100}}{x} + \dfrac{{100}}{{x + 10}} - \dfrac{{11}}{3} = 0\\ \Leftrightarrow 300\left( {x + 10} \right) + 300x - 11x\left( {x + 10} \right) = 0\\ \Leftrightarrow 600x + 3000 - 11{x^2} - 110x = 0\\ \Leftrightarrow 11{x^2} - 490x - 3000 = 0\\ \Leftrightarrow \left( {x - 50} \right)\left( {11x + 60} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 50 = 0\\11x + 60 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 50\;\;\left( {tm} \right)\\x =  - \dfrac{{60}}{{11}}\;\;\left( {ktm} \right)\end{array} \right..\end{array}$

Vậy vận tốc của ô tô lúc đi là $50\;km/h.$

2) Tìm $m$ để phương trình ${x^2} - 2mx + {m^2} - 2 = 0$ (x là ẩn, m là tham số) có hai nghiệm phân biệt ${x_1},\;{x_2}$ thỏa mãn $\left| {x_1^3 - x_2^3} \right| = 10\sqrt 2 .$

Phương trình có hai nghiệm phân biệt $\Leftrightarrow \Delta ' > 0 \Leftrightarrow {m^2} - {m^2} + 2 > 0\;$$\Leftrightarrow 2 > 0\;\forall m$

$\Rightarrow$ Phương trình luôn có hai nghiệm ${x_1},\;\;{x_2}$ với mọi $m.$

Áp dụng hệ thức Vi-ét ta có: $\left\{ \begin{array}{l}{x_1} + {x_2} = 2m\\{x_1}{x_2} = {m^2} - 2\end{array} \right..$

Theo đề bài ta có: $\left| {x_1^3 - x_2^3} \right| = 10\sqrt 2$

$\begin{array}{l} \Leftrightarrow \left| {\left( {{x_1} - {x_2}} \right)\left( {x_1^2 + {x_1}{x_2} + x_2^2} \right)} \right| = 10\sqrt 2 \\ \Leftrightarrow \left| {\left( {{x_1} - {x_2}} \right)\left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - {x_1}{x_2}} \right]} \right| = 10\sqrt 2 \\ \Leftrightarrow {\left| {\left( {{x_1} - {x_2}} \right)\left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - {x_1}{x_2}} \right]} \right|^2} = 200\\ \Leftrightarrow {\left( {{x_1} - {x_2}} \right)^2}{\left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - {x_1}{x_2}} \right]^2} = 200\\ \Leftrightarrow \left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - 4{x_1}{x_2}} \right]{\left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - {x_1}{x_2}} \right]^2} = 200\\ \Leftrightarrow \left[ {4{m^2} - 4\left( {{m^2} - 2} \right)} \right]{\left[ {4{m^2} - {m^2} + 2} \right]^2} = 200\\ \Leftrightarrow 8{\left( {3{m^2} + 2} \right)^2} = 200\\ \Leftrightarrow {\left( {3{m^2} + 2} \right)^2} = 25\\ \Leftrightarrow 3{m^2} + 2 = 5\;\;\;\left( {do\;\;3{m^2} + 2 > 0\;\;\forall m} \right)\\ \Leftrightarrow {m^2} = 1\\ \Leftrightarrow m =  \pm 1.\end{array}$

Vậy $m =  \pm 1$ thỏa mãn bài toán.

Câu 4:

Cho tam giác ABC nội tiếp đường tròn tâm O đường kính BC. Kẻ AH vuông góc với BC (H thuộc BC), gọi M, N lần lượt là hình chiếu vuông góc của H trên AB và AC.

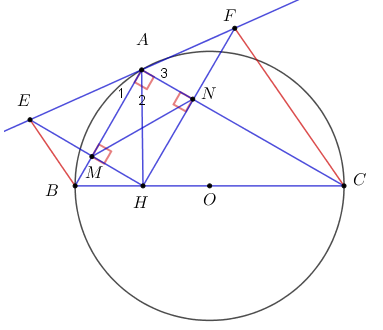
1) Chứng minh $A{C^2} = CH.CB.$

Xét đường tròn ngoại tiếp tam giác ABC có đường kính BC ta có:

$\widehat {BAC}$ là góc nội tiếp chắn nửa đường tròn $\Rightarrow \widehat {BAC} = {90^0} \Rightarrow$ $\Delta ABC$ vuông tại $A.$

Xét tam giác $ABC$ có đường cao ta có:

$A{C^2} = CH.CB$ (hệ thức lượng trong tam giác vuông). (đpcm)

2) Chứng minh tứ giác $BCNM$ nội tiếp và $AC.BM + AB.CN = AH.BC.$

+) Ta có $ANHM$ là hình chữ nhật do có 3 góc vuông.

$\Rightarrow AN//MH,\;\;AM//HN.$

$\Rightarrow \widehat {MAH} = \widehat {AMN}$ (tính chất).

Lại có 

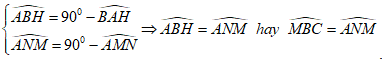
Xét tứ giác $BCNM$ ta có: $\widehat {MBC} = \widehat {ANM}\;\;\left( {cmt} \right)$

$\Rightarrow BMNC$ là tứ giác nội tiếp (góc trong tại một đỉnh bằng góc ngoài tại đỉnh đối diện).

+) Xét $\Delta BMH$ và $\Delta AHC$ ta có:

$\widehat {MBH} = \widehat {HAC}\;\;$(cùng phụ với $\widehat {ACH}$)

$\begin{array}{l}\widehat {BMH} = \widehat {AHC} = {90^0}\\ \Rightarrow \Delta BMH \sim \Delta AHC\;\;\left( {g - g} \right)\\ \Rightarrow \dfrac{{BM}}{{AH}} = \dfrac{{BH}}{{AC}} \\\Leftrightarrow AC.BM = AH.BH.\end{array}$

Xét $\Delta CNH$ và $\Delta BAH$ ta có:

$\widehat {NCH} = \widehat {BAH}$ (cùng phụ với $\widehat {ABH}$)

$\begin{array}{l}\widehat {CNH} = \widehat {AHB} = {90^0}\\ \Rightarrow \Delta CNH \sim \Delta AHB\left( {g - g} \right)\\ \Rightarrow \dfrac{{CN}}{{AH}} = \dfrac{{CH}}{{AB}}\\ \Rightarrow AB.CN = AH.CH.\end{array}$

$\Rightarrow AC.BM + AB.CN = AH.BH + AH.CH$$\,= AH\left( {BH.CH} \right) = AH.BC\;\;\left( {dpcm} \right)$

3) Đường thẳng đi qua A cắt tia HM tại E và cắt tia đối của tia NH tại F. Chứng minh BE // CF.

Ta có :

$\Delta ANF \sim \Delta EMA\left( {g - g} \right)$

$\Rightarrow \dfrac{{AN}}{{ME}} = \dfrac{{NF}}{{AM}}$$\;\Rightarrow AN.AM = NF.ME\,\,\left( 1 \right)$

Lại có : $\begin{array}{l}\Delta BMH \sim \Delta HNC\left( {g - g} \right)\\ \Rightarrow \dfrac{{BM}}{{HN}} = \dfrac{{MH}}{{NC}} \\\Rightarrow BM.NC = MH.HN\,\,\left( 2 \right)\end{array}$

Mặt khác $AM.AN = MH.NH\,\,\left( {AM = NH;AN = MH} \right)\,\,\,\left( 3 \right)$

Từ (1) , (2), (3)  suy ra $NF.ME = BM.NC \Rightarrow \dfrac{{NF}}{{NC}} = \dfrac{{BM}}{{ME}}$ $\Rightarrow \dfrac{{ME}}{{NC}} = \dfrac{{BM}}{{NF}}$

Mà $\widehat {BME} = \widehat {CNF} = {90^0}$

Suy ra $\Delta BME \sim \Delta FNC\left( {c - g - c} \right)$ $\Rightarrow \widehat {CFN} = \widehat {EBM}$

Ta lại có $\widehat {NFA} = \widehat {MEA}\left( {Do\,\,AB\parallel HF} \right)$

Nên ta có : $\begin{array}{l}\widehat {CFE} + \widehat {BEF} = \widehat {CFN} + \widehat {NFA} + \widehat {BEF} = \widehat {EBM} + \widehat {MAE} + \widehat {BEF}\\ \Rightarrow \widehat {CFE} + \widehat {BEF} = \widehat {EBA} + \widehat {BAE} + \widehat {BEF} = {180^0}\end{array}$

(Theo định lý tổng ba góc trong tam giác EBA).

Vậy BE//CF

Câu 5:

Phương trình có hai nghiệm ${x_1},\;{x_2}$ thỏa mãn $0 \le {x_1} \le {x_2} \le 2$

$\Leftrightarrow \left\{ \begin{array}{l}\Delta  \ge 0\\af\left( 0 \right) \ge 0\\af\left( 2 \right) \ge 0\\\dfrac{S}{2} > 0\\\dfrac{S}{2} < 2\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}{b^2} - 4ac > 0\\ac \ge 0\\a\left( {4a + 2b + c} \right) \ge 0\\ - \dfrac{b}{{2a}} > 0\\ - \dfrac{b}{{2a}} < 2\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}{b^2} \ge 4ac\\ac \ge 0\\a\left( {4a + 2b + c} \right) \ge 0\\\dfrac{b}{{2a}} < 0\\\dfrac{{4a + b}}{{2a}} > 0\end{array} \right..$

Theo hệ thức Vi-ét ta có: $\left\{ \begin{array}{l}{x_1} + {x_2} =  - \dfrac{b}{a}\\{x_1}{x_2} = \dfrac{c}{a}\end{array} \right..$

Theo đề bài ta có:

$\begin{array}{l}L = \dfrac{{3{a^2} - ab + ac}}{{5{a^2} - 3ab + {b^2}}} \\\;\;= \dfrac{{3 - \dfrac{b}{a} + \dfrac{c}{a}}}{{5 - 3.\dfrac{b}{a} + {{\left( {\dfrac{b}{a}} \right)}^2}}}\;\;\left( {do\;\;a \ne 0} \right)\\\;\; = \dfrac{{3 + \left( {{x_1} + {x_2}} \right) + {x_1}{x_2}}}{{5 + 3\left( {{x_1} + {x_2}} \right) + {{\left( {{x_1} + {x_2}} \right)}^2}}}\;\;\;\left( {L > 0\;\;\forall \;0 \le {x_1} \le {x_2} \le 2} \right)\\\;\; = \dfrac{{3 + {x_1} + {x_2} + {x_1}{x_2}}}{{5 + 3{x_1} + 3{x_2} + x_1^2 + x_2^2 + 2{x_1}{x_2}}}.\\ \Rightarrow \dfrac{1}{L} = \dfrac{{5 + 3{x_1} + 3{x_2} + x_1^2 + x_2^2 + 2{x_1}{x_2}}}{{3 + {x_1} + {x_2} + {x_1}{x_2}}}.\end{array}$

Vì $0 \le {x_1} \le {x_2} \le 2 \Rightarrow \left\{ \begin{array}{l}x_1^2 \le 2{x_1}\\x_2^2 \le 2{x_2}\\{x_1} - 2 \le 0\\{x_2} - 2 \le 0\end{array} \right.$ $\Rightarrow \left\{ \begin{array}{l}x_1^2 + x_2^2 \le 2{x_1} + 2{x_2}\\\left( {{x_1} - 2} \right)\left( {{x_2} - 2} \right) \ge 0\end{array} \right..$

$\begin{array}{l} \Rightarrow \dfrac{1}{L} \le \dfrac{{5 + 3{x_1} + 3{x_2} + 2{x_1} + 2{x_2} + 2{x_1}{x_2}}}{{3 + {x_1} + {x_2} + {x_1}{x_2}}}\\\;\;\;\;\;\;\; = \dfrac{{5 + 5{x_1} + 5{x_2} + 2{x_1}{x_2}}}{{3 + {x_1} + {x_2} + {x_1}{x_2}}}\\\;\;\;\;\;\;\; = \dfrac{{3{x_1}{x_2} + 3{x_1} + 3{x_2} + 9 - {x_1}{x_2} + 2{x_1} + 2{x_2} - 4}}{{3 + {x_1} + {x_2} + {x_1}{x_2}}}\\\;\;\;\;\;\;\; = \dfrac{{3\left( {3 + {x_1} + {x_2} + {x_1}{x_2}} \right) - \left( {{x_2} - 2} \right){x_1} + 2\left( {{x_2} - 2} \right)}}{{3 + {x_1} + {x_2} + {x_1}{x_2}}}\\\;\;\;\;\;\;\; = 3 - \dfrac{{\left( {{x_2} - 2} \right)\left( {{x_1} - 2} \right)}}{{3 + {x_1} + {x_2} + {x_1}{x_2}}} \le 3\;\;\;\left( {do\;\;\left( {{x_2} - 2} \right)\left( {{x_1} - 2} \right) \ge 0} \right)\\ \Rightarrow 0 \le \dfrac{1}{L} \le 3 \Leftrightarrow 3L \ge 1 \Leftrightarrow L \ge \dfrac{1}{3}\\ \Rightarrow Min\;L = \dfrac{1}{3}.\end{array}$

Dấu “=” xảy ra

$\Leftrightarrow \left\{ \begin{array}{l}x_1^2 = 2{x_1}\\x_2^2 = 2{x_2}\\\left( {{x_1} - 2} \right)\left( {{x_2} - 2} \right) = 0\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}{x_1}\left( {{x_1} - 2} \right) = 0\\{x_2}\left( {{x_2} - 2} \right) = 0\\\left[ \begin{array}{l}{x_1} - 2 = 0\\{x_2} - 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{x_1} = 2\\{x_2} = 2\end{array} \right.\end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}{x_1} = 0\\{x_1} = 2\end{array} \right.\\\left[ \begin{array}{l}{x_2} = 0\\{x_2} = 2\end{array} \right.\\\left[ \begin{array}{l}{x_1} = 2\\{x_2} = 2\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}{x_1} = 0\\{x_2} = 2\end{array} \right.\\\left\{ \begin{array}{l}{x_1} = 2\\{x_2} = 0\end{array} \right.\\\left\{ \begin{array}{l}{x_1} = 2\\{x_2} = 2\end{array} \right.\end{array} \right..$

Vậy $Min\;L = \dfrac{1}{3}$ khi $\left( {{x_1};\;{x_2}} \right) = \left\{ {\left( {0;\;2} \right),\;\left( {2;\;0} \right),\;\left( {2;\;2} \right)} \right\}.$

Loigiaihay.com