Đề thi toán 7, đề kiểm tra toán 7 kết nối tri thức với cuộc sống có đáp án và lời giải chi tiết
Đề thi toán 7, đề kiểm tra toán 7 kết nối tri thức với cuộc sống có đáp án và lời giải chi tiết
 Đề thi giữa kì 2 Toán 7 Kết nối tri thức
Đề thi giữa kì 2 Toán 7 Kết nối tri thức Đề thi giữa kì 2 Toán 7 - Đề số 1 - Kết nối tri thức
Tải vềI. TRẮC NGHIỆM ( 2 điểm) Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Đề bài
I. TRẮC NGHIỆM ( 2 điểm)
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1. Nếu tam giác \(ABC\) cân tại B thì
A. Đường trung tuyến AM đồng thời là đường phân giác
B. Đường trung tuyến CP đồng thời là đường trung trực
C. Đường trung tuyến BN đồng thời là đường phân giác
D. Đường trung tuyến AM đồng thời là đường trung trực
Câu 2. Cho \(\Delta ABC\) có \(\angle A = {50^0}\,,\,\angle B = {90^0}\) thì quan hệ giữa ba cạnh \(AB,AC,BC\) là:
A. \(BC > AC > AB\)
B. \(AB > BC > AC\)
C. \(AB > AC > BC\)
D. \(AC > BC > AB\)
Câu 3. Cho biết \(x\) và \(y\) là hai đại lượng tỉ lệ thuận, biết khi \(x = 5\) thì \(y = 10\). Vậy khi \(x = 2\) thì \(y\) bằng bao nhiêu?
A. \(4\)
B. \(25\)
C. \(10\)
D.\(20\)
Câu 4. Cho x và y là hai đại lượng tỉ lệ nghịch với nhau và khi x = –21 thì y = 12. Khi x = 7 thì y bằng:
A. –36;
B. 36;
C. –4;
D. 4.
Câu 5. Biểu thức đại số biểu thị “Tổng lập phương của hai số x và y” là
A. x3 – y3;
B. x + y;
C. x3 + y3;
D. (x + y)3.
Câu 6. Hệ số cao nhất của đa thức M = 10x2 – 4x + 3 – 5x5 là
A. 10;
B. -4;
C. 3;
D. -5.
Câu 7. Cho tam giác ABC, đường trung tuyến AM = 9 cm. Gọi G là trọng tâm của tam giác. Tính độ dài GM?
A. GM = 6 cm;
B. GM = 9 cm;
C. GM = 3 cm;
D. GM = 18 cm.
Câu 8. Bộ ba độ dài đoạn thẳng nào sau đây không thể tạo thành một tam giác?
A. 8cm; 9cm; 10cm;
B. 3cm; 4cm; 5cm;
C. 1cm; 2cm; 3cm;
D. 11cm; 9cm; 7cm.
II. PHẦN TỰ LUẬN (8,0 điểm)
Bài 1. (1 điểm) Tìm \(x\) biết:
a) \(\dfrac{1}{{12}} + x = \dfrac{{ - 11}}{{12}}\)
b) \(\dfrac{{2x - 1}}{{27}} = \dfrac{3}{{2x - 1}}\)
Bài 2. (1,5 điểm) Ba đội công nhân tham gia làm đường và phải làm ba khối lượng công việc như nhau. Để hoàn thành công việc, đội I cần 4 ngày, đội II cần 6 ngày và đội III cần 8 ngày. Tính số công nhân của mỗi đội, biết rằng đội I có nhiều hơn đội II là 4 người (năng suất mỗi người như nhau).
Bài 3. (1,5 điểm) Cho các đa thức:
\(A\left( x \right) = 2\,{x^4} - 5\,{x^3} + 7\,x - 5 + 4\,{x^3} + 3\,{x^2} + 2\,x + 3\)
\(B\left( x \right) = 5\,{x^4} - 3\,{x^3} + 5\,x - 3\,{x^4} - 2\,{x^3}\, + 9 - 6\,x\)
\(C\left( x \right) = {x^4} + 4\,{x^2} + 5\)
a) Thu gọn và sắp xếp các hạng tử của đa thức \(A\left( x \right),\,B\left( x \right)\) theo lũy thừa giảm dần của biến.
b) Tính \(A\left( x \right) + B\left( x \right);\,A\left( x \right) - B\left( x \right)\).
c) Chứng minh rằng đa thức \(C\left( x \right)\) không có nghiệm.
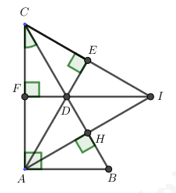
Bài 4. (3,5 điểm) Cho \(\Delta ABC\) vuông tại \(A\) có \(\angle C = {30^0},\) đường cao \(AH.\) Trên đoạn \(HC\) lấy điểm \(D\) sao cho \(HD = HB.\)
a) Chứng minh \(\Delta AHB = \Delta AHD\).
b) Chứng minh \(\Delta ABD\) là tam giác đều.
c) Từ \(C\) kẻ \(CE\) vuông góc với đường thẳng \(AD\)\(\left( {E \in \,AD} \right)\). Chứng minh \(DE = HB\).
d) Từ \(D\) kẻ \(DF\) vuông góc với \(AC\) (\(F\,\)thuộc \(AC\)), \(I\) là giao điểm của \(CE\) và \(AH.\) Chứng minh ba điểm \(I,\,D,\,F\) thẳng hàng.
Bài 5. (0,5 điểm)
Cho \(a,b,c\) là các số thực khác không \(\left( {b \ne c} \right)\) và \(\dfrac{1}{c} = \dfrac{1}{2}\left( {\dfrac{1}{a} + \dfrac{1}{b}} \right)\). Chứng minh rằng: \(\dfrac{a}{b} = \dfrac{{a - c}}{{c - b}}\).
Lời giải
I. Trắc nghiệm:
|
1. C |
2. D |
3. A |
4. A |
|
5. C |
6. D |
7. C |
8. C |
Câu 1:
Phương pháp:
Trong tam giác cân, đường trung tuyến ứng với đỉnh cân đồng thời là đường trung trực, đường cao, đường phân giác.
Cách giải:
Tam giác ABC cân tại B nên đường trung tuyến BN đồng thời là đường phân giác.
Chọn C.
Câu 2:
Phương pháp: Dựa vào mối quan hệ giữa góc và cạnh trong tam giác để so sánh các cạnh với nhau.
Cách giải:
Ta có: \(\angle C = {180^0} - \left( {{{50}^0} + {{90}^0}} \right) = {40^0}\).
\( \Rightarrow \angle C < \angle A < \angle B\)
\( \Rightarrow AB < BC < AC\) hay \(AC > BC > AB\).
Chọn D.
Câu 3:
Phương pháp:
Tính chất hai đại lượng tỉ lệ thuận
Cách giải:
\(x\) và \(y\) là hai đại lượng tỉ lệ thuận \( \Rightarrow y = ax\left( {a \ne 0} \right)\)
Thay \(x = 5;y = 10\) vào ta được: \(10 = a.5 \Rightarrow a = 2\)
Vậy hệ số tỉ lệ của \(y\) đối với \(x\) là \(a = 2\).
Ta có: \(y = 2x\), khi \(x = 2\) thì \(y = 2.2 = 4\).
Chọn A.
Câu 4:
Phương pháp:
Tính chất hai đại lượng tỉ lệ nghịch: tích 2 giá trị tương ứng của 2 đại lượng luôn không đổi (bằng hệ số tỉ lệ)
Cách giải:
Hệ số tỉ lệ là: -21 . 12 = -252.
Khi x = 7 thì y = -252 : 7 = -36.
Chọn A
Câu 5:
Phương pháp:
Mô tả
Cách giải:
Tổng lập phương của hai số x và y là x3 + y3
Câu 6:
Phương pháp:
Hệ số cao nhất của đa thức là hệ số của hạng tử có bậc cao nhất trong đa thức.
Cách giải:
Đa thức M = 10x2 – 4x + 3 – 5x5 có hệ số cao nhất là -5.
Chọn D
Chú ý: Hệ số cao nhất không phải hệ số lớn nhất trong đa thức.
Câu 7:
Phương pháp: Nếu \(\Delta ABC\) có trung tuyến \(AM\) và trọng tâm \(G\) thì \(AG = \dfrac{2}{3}AM\).
Cách giải:
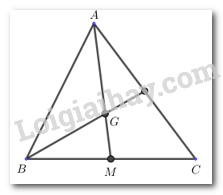
Nếu \(\Delta ABC\) có trung tuyến \(AM\) và trọng tâm \(G\) thì \(GM = \dfrac{1}{3}AM = \dfrac{1}{3}.9 = 3(cm)\).
Chọn C.
Câu 8:
Phương pháp: Bất đẳng thức tam giác: Kiểm tra tổng độ dài 2 cạnh nhỏ hơn có lớn hơn độ dài cạnh lớn nhất không. Nếu không thì bộ 3 độ dài đó không tạo được thành tam giác.
Cách giải:
Vì 1 + 2 = 3 nên không thỏa mãn bất đẳng thức tam giác.
Chọn C.
II. TỰ LUẬN
Bài 1:
Phương pháp:
a) Thực hiện các phép toán với phân số.
b) Vận dụng định nghĩa hai phân số bằng nhau: Nếu \(\dfrac{a}{b} = \dfrac{c}{d}\) thì \(ad = bc\).
Cách giải:
a) \(\dfrac{1}{{12}} + x = \dfrac{{ - 11}}{{12}}\)
\(\begin{array}{l}x = \dfrac{{ - 11}}{{12}} - \dfrac{1}{{12}}\\x = \dfrac{{ - 11 - 1}}{{12}}\\x = \dfrac{{ - 12}}{{12}} = - 1\end{array}\)
Vậy \(x = - 1\)
b) \(\dfrac{{2x - 1}}{{27}} = \dfrac{3}{{2x - 1}}\)
\(\begin{array}{l}{\left( {2x - 1} \right)^2} = 27.3 = 81\\{\left( {2x - 1} \right)^2} = {\left( { \pm 9} \right)^2}\end{array}\)
Trường hợp 1:
\(\begin{array}{l}2x - 1 = 9\\2x = 10\\x = 5\end{array}\)
Trường hợp 2:
\(\begin{array}{l}2x - 1 = - 9\\2x = - 8\\x = - 4\end{array}\)
Vậy \(x \in\){ 5; - 4}
Bài 2:
Phương pháp:
Gọi số công nhân của 3 đội lần lượt là \(x,y,z\) (điều kiện: \(x,y,z \in {\mathbb{N}^*}\))
Vận dụng kiến thức về tỉ lệ nghịch để tìm các đại lượng của đề bài.
Cách giải:
Gọi số công nhân của 3 đội lần lượt là \(x,y,z\) (điều kiện: \(x,y,z \in {\mathbb{N}^*}\))
Vì đội I có nhiều hơn đội II là \(4\) người nên: \(x - y = 4\)
Vì số năng suất mỗi người là như sau, nên số người và số ngày hoàn thành công việc là hai đại lượng tỉ lệ nghịch, nên ta có:
\(4x = 6y = 8z\) hay \(\dfrac{x}{{\dfrac{1}{4}}} = \dfrac{y}{{\dfrac{1}{6}}} = \dfrac{z}{{\dfrac{1}{8}}}\)
Theo tính chất của dãy tỉ số bằng nhau, ta có: \(\dfrac{x}{{\dfrac{1}{4}}} = \dfrac{y}{{\dfrac{1}{6}}} = \dfrac{z}{{\dfrac{1}{8}}} = \dfrac{{x - y}}{{\dfrac{1}{4} - \dfrac{1}{6}}} = \dfrac{4}{{\dfrac{1}{{12}}}} = 48\)
Từ \(\dfrac{x}{{\dfrac{1}{4}}} = 48 \Rightarrow x = 12\) (tmđk)
\(\dfrac{y}{{\dfrac{1}{6}}} = 48 \Rightarrow y = 8\) (tmđk)
\(\dfrac{z}{{\dfrac{1}{8}}} = 48 \Rightarrow z = 6\) (tmđk)
Vậy số công nhân của \(3\) đội lần lượt là: \(12\) công nhân, \(8\) công nhân, \(6\) công nhân.
Bài 3:
Phương pháp:
a) Thu gọn và sắp xếp các hạng tử của đa thức \(A\left( x \right),\,B\left( x \right)\) theo lũy thừa giảm dần của biến.
b) Tính \(A\left( x \right) + B\left( x \right);\,A\left( x \right) - B\left( x \right)\).
c) Chứng minh rằng đa thức \(C\left( x \right)\) không có nghiệm.
Cách giải:
a) Thu gọn:
\(\begin{array}{l}A\left( x \right) = 2\,{x^4} - 5\,{x^3} + 7\,x - 5 + 4\,{x^3} + 3\,{x^2} + 2\,x + 3\\A\left( x \right) = 2\,{x^4} + \left( { - 5\,{x^3} + 4\,{x^3}} \right) + 3{x^2} + \left( {7\,x + 2\,x} \right) - 5 + 3\\A\left( x \right) = 2\,{x^4} - {x^3} + 3\,{x^2} + 9\,x\, - 2\end{array}\)
\(\begin{array}{l}B\left( x \right) = 5\,{x^4} - 3\,{x^3} + 5\,x - 3\,{x^4} - 2\,{x^3}\, + 9 - 6\,x\\B\left( x \right) = \left( {5\,{x^4} - 3\,{x^4}} \right) + \left( { - 3\,{x^3} - 2\,{x^3}} \right) + \left( {5\,x - 6\,x} \right) + 9\\B\left( x \right) = \,\,\,\,\,\,2\,{x^4}\, - \,5{x^3} - x + 9\end{array}\)
b) Tính \(A\left( x \right) + B\left( x \right);\,A\left( x \right) - B\left( x \right)\).
\(\begin{array}{l} + )\,A\left( x \right) + B\left( x \right) = \left( {2\,{x^4} - {x^3} + 3\,{x^2} + 9\,x - 2} \right) + \left( {2\,{x^4} - 5\,{x^3} - x + 9} \right)\\ = \left( {2\,{x^4} + 2\,{x^4}} \right) + \left( { - {x^3} - 5\,{x^3}} \right) + 3\,{x^2} + \left( {9\,x - x} \right) + \left( { - 2 + 9} \right)\\ = \,\,\,4\,{x^4} - 6\,{x^3} + 3\,{x^2} + 8\,x + 7\end{array}\)
\(\begin{array}{l} + )\,A\left( x \right) - B\left( x \right) = \left( {2\,{x^4} - {x^3} + 3\,{x^2} + 9\,x - 2} \right) - \left( {2\,{x^4} - 5\,{x^3} - x + 9} \right)\\ = \left( {2\,{x^4} - \,{x^3} + 3\,{x^2} + 9\,x - 2} \right) - 2\,{x^4} + 5\,{x^3} + x - 9\\ = \left( {2\,{x^4} - \,2\,{x^4}} \right) + \left( { - {x^3} + 5\,{x^3}} \right) + 3\,{x^2} + \left( {9\,x + x} \right) + \left( { - 2 - 9} \right)\\ = \,\,\,\,\,\,\,\,\,\,4\,{x^3} + \,3\,{x^2} + 10\,x - 11\end{array}\)
c) Chứng minh rằng đa thức \(C\left( x \right)\) không có nghiệm.
Ta có: \(C\left( x \right) = {x^4} + 4\,{x^2} + 5\).
Vì \({x^4}\, > 0,\,\,\forall \,x\) và \({x^2} > 0,\,\forall \,x\) nên \(C\left( x \right) > 0,\,\,\forall \,x.\)
\( \Rightarrow \) không có giá trị nào của \(x\) làm cho \(C\left( x \right) = 0\).
\( \Rightarrow \,C\left( x \right)\) là đa thức không có nghiệm.
Bài 4: Phương pháp:
a) Chứng minh hai tam giác bằng nhau theo trường hợp c.g.c.
b) Chứng minh \(\Delta ABD\)là tam giác cân có một góc bằng \({60^0}\), rồi suy ra \(\Delta ABD\) là tam giác đều.
c) Chứng minh \(DE = DH\) (hai cạnh tương ứng). Mà \(DH = DB\) (giả thiết) \( \Rightarrow DE = DB\).
d) Chứng minh DF và IF cùng vuông góc với AC nên DI trùng với DF hay I, D, F thẳng hàng.
Cách giải:
a) Xét \(\Delta AHB\) và \(\Delta AHD\) ta có:
\(HD = HB\) (gt)
\(AH\,\,chung\)
\(\angle AHB = \angle AHD = {90^0}\)
\( \Rightarrow \)\(\Delta AHB = \,\Delta AHD\) (c.g.c)
b) \(\Delta ABC\) vuông tại \(A\),
có \(\angle C = {30^0} \Rightarrow \angle B = {90^0} - {30^0} = {60^0}\) (định lý tổng ba góc của một tam giác).
Vì \(\Delta AHB = \,\Delta AHD\) (cmt)
\( \Rightarrow AB = AD\) (hai cạnh tương ứng).
\( \Rightarrow \Delta ABD\) cân tại \(A\) mà \(\angle B = {60^0}\)
Do đó: \(\Delta ABD\)là tam giác đều.
c) Vì \(\Delta ABD\)là tam giác đều (cmt)
\( \Rightarrow \angle DAB = {60^0}\)
\(\begin{array}{l} \Rightarrow \angle CAD = {90^0} - \angle DAB\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {90^0} - {60^0}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {30^0}\end{array}\)
Xét \(\Delta ACD\) có \(\angle ACD = \angle \,CAD = {30^0}\).
\( \Rightarrow \Delta ACD\) cân tại \(D.\)
\( \Rightarrow \,CD = AD\)
Xét \(\Delta DEC\) và \(\Delta DHA\) có:
\(CD = AD\,\,\left( {cmt} \right)\)
\(\angle E = \angle H = {90^0}\)
\(\angle CDE = \angle ADH\) (đối đỉnh)
\( \Rightarrow \,\Delta DEC = \Delta DHA\) (cạnh huyền – góc nhọn).
\( \Rightarrow DE = DH\) (hai cạnh tương ứng).
Mà \(DH = DB\) (giả thiết)
\( \Rightarrow DE = DB\).
d) Xét \(\Delta CED\) và \(\Delta AHD\) có:
HD = HB (gt)
Mà DE = BH nên DE = DH.
\(\Delta CED = \Delta AHD\) (cạnh góc vuông - góc nhọn)
suy ra CE = AH, CD = DA, \(\widehat{DCE} = \widehat{DAH}\)
Vì CD = DA nên tam giác CDA cân, do đó \(\widehat{DCF} = \widehat{DAF}\)
Xét tam giác CDF và tam giác ADF có:
CD = AD
FD chung
\(\widehat{CFD} = \widehat{AFD} (=90^\circ)\)
nên \(\Delta CDF = \Delta ADF\) (cạnh huyền - cạnh góc vuông)
suy ra CF = FA.
Suy ra \(\widehat{DCE}+\widehat{DCF} = \widehat{DAH}+\widehat{DAF}\)
hay \(\widehat{ECF} = \widehat{HAF}\)
Suy ra tam giác ACI cân tại I.
Suy ra \(CI = IA\)
Xét tam giác CIF và tam giác AIF có:
CI = AI (cmt)
IF chung
CF = FA (cmt)
suy ra \(\Delta CIF = \Delta AIF\) (c.c.c)
suy ra \(\widehat{CFI} = \widehat{AFI}\)
Mà hai góc này là hai góc kề bù nên \(\widehat{CFI} = \widehat{AFI} = \frac{180^\circ}{2} = 90^\circ\) hay \(IF \bot CA\)
Mà \(DF \bot AC\) nên DF và IF trùng nhau, hay I, D, F thẳng hàng.
Câu 5:
Phương pháp:
Vận dụng định nghĩa hai phân số bằng nhau để chứng minh.
Cách giải:
Ta có: \(\dfrac{1}{c} = \dfrac{1}{2}\left( {\dfrac{1}{a} + \dfrac{1}{b}} \right)\)
\(\begin{array}{l} \Rightarrow \dfrac{1}{c} = \dfrac{{a + b}}{{2ab}}\\ \Rightarrow 2ab = ac + bc\\ \Rightarrow ab + ab = ac + bc\\ \Rightarrow ab - bc = ac - ab\\ \Rightarrow b\left( {a - c} \right) = a\left( {c - b} \right)\end{array}\)
\( \Rightarrow \dfrac{a}{b} = \dfrac{{a - c}}{{c - b}}\) (đpcm)
- Đề thi giữa kì 2 Toán 7 - Đề số 2 - Kết nối tri thức
- Đề thi giữa kì 2 Toán 7 - Đề số 3 - Kết nối tri thức
- Đề thi giữa kì 2 Toán 7 - Đề số 4 - Kết nối tri thức
- Đề thi giữa kì 2 Toán 7 - Đề số 5 - Kết nối tri thức
- Đề thi giữa kì 2 Toán 7 Kết nối tri thức - Đề số 6
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 7 - Kết nối tri thức - Xem ngay