 Toán 11, giải toán lớp 11 kết nối tri thức với cuộc sống
Toán 11, giải toán lớp 11 kết nối tri thức với cuộc sống
 Bài tập cuối chương 4 Toán 11 kết nối tri thức
Bài tập cuối chương 4 Toán 11 kết nối tri thức
Bài 4.39 trang 102 SGK Toán 11 tập 1 - Kết nối tri thức
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh SB, SD; K là giao điểm của mặt phẳng (AMN) và đường thẳng SC. Tỉ số (frac{{SK}}{{SC}}) bằng: A. (frac{1}{2}) B. (frac{1}{3}) C. (frac{1}{4}) D. (frac{2}{3})
Đề bài
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh SB, SD; K là giao điểm của mặt phẳng (AMN) và đường thẳng SC. Tỉ số \(\frac{{SK}}{{SC}}\) bằng:
A. \(\frac{1}{2}\)
B. \(\frac{1}{3}\)
C. \(\frac{1}{4}\)
D. \(\frac{2}{3}\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng định lý Menelaus để tính tỉ số.
Lời giải chi tiết
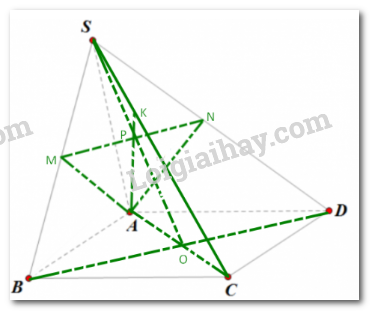
Gọi O là giao điểm AC và BD, gọi P là trung điểm MN
Ta có MN là đường trung bình tam giác SBD
Suy ra S, P, O thẳng hàng và P là trung điểm của SO.
Do đó P thuộc SO hay P thuộc mp(SAC).
Trong mp(SAC), nối AP kéo dài cắt SC tại K.
Suy ra K là giao điểm của SC và mp(AMN).
Áp dụng định lí Menelaus cho tam giác SOC:
\(\frac{{KS}}{{KC}} . \frac{{CA}}{{AO}} .\frac{{OP}}{{PS}} = 1\) suy ra \(\frac{{KS}}{{KC}} . \frac{2}{1} . 1 = 1\) suy ra \(\frac{{KS}}{{KC}} = \frac{1}{2}\).
Vậy \(\frac{{SK}}{{SC}} = \frac{1}{3}\).
Đáp án: B
- Bài 4.40 trang 102 SGK Toán 11 tập 1 - Kết nối tri thức
- Bài 4.41 trang 103 SGK Toán 11 tập 1 - Kết nối tri thức
- Bài 4.42 trang 103 SGK Toán 11 tập 1 - Kết nối tri thức
- Bài 4.43 trang 103 SGK Toán 11 tập 1 - Kết nối tri thức
- Bài 4.44 trang 103 SGK Toán 11 tập 1 - Kết nối tri thức
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Kết nối tri thức - Xem ngay
Các bài khác cùng chuyên mục
- Giải câu hỏi mở đầu trang 119 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 111 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 95 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 88 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 84 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 119 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 111 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 95 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 88 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 84 SGK Toán 11 tập 1 - Kết nối tri thức












Danh sách bình luận