Bài 3 trang 106 SGK Toán 11 tập 2 - Cánh Diều

Với giả thiết ở Bài tập 2, hãy:

Tổng hợp đề thi học kì 2 lớp 11 tất cả các môn - Cánh diều

Toán - Văn - Anh - Lí - Hóa - Sinh

Đề bài

Với giả thiết ở Bài tập 2, hãy:

a) Chứng minh rằng \(MN\parallel BC\). Tính khoảng cách giữa hai đường thẳng \(MN\) và \(BC\).

b) Chứng minh rằng \(MP\parallel \left( {BCD} \right)\). Tính khoảng cách từ đường thẳng \(MP\) đến mặt phẳng \(\left( {BCD} \right)\).

c) Chứng minh rằng \(\left( {MNP} \right)\parallel \left( {BCD} \right)\). Tính khoảng cách giữa hai mặt phẳng \(\left( {MNP} \right)\) và \(\left( {BCD} \right)\).

Phương pháp giải - Xem chi tiết

a) ‒ Sử dụng tính chất đường trung bình của tam giác.

‒ Cách tính khoảng cách giữa hai đường thẳng song song: Tính khoảng cách từ một điểm thuộc đường thẳng này đến đường thẳng kia.

b) ‒ Cách chứng minh đường thẳng song song với mặt phẳng: Chứng minh đường thẳng đó song song với một đường thẳng nằm trên mặt phẳng.

‒ Cách tính khoảng cách giữa đường thẳng và mặt phẳng song song: Tính khoảng cách từ một điểm trên đường thẳng đến mặt phẳng.

c) ‒ Cách chứng minh hai mặt phẳng song song: Chứng minh mặt phẳng này chứa hai đường thẳng cắt nhau song song với mặt phẳng còn lại.

‒ Cách tính khoảng cách giữa hai mặt phẳng song song: Tính khoảng cách từ một điểm trên mặt phẳng này đến mặt phẳng còn lại.

Lời giải chi tiết

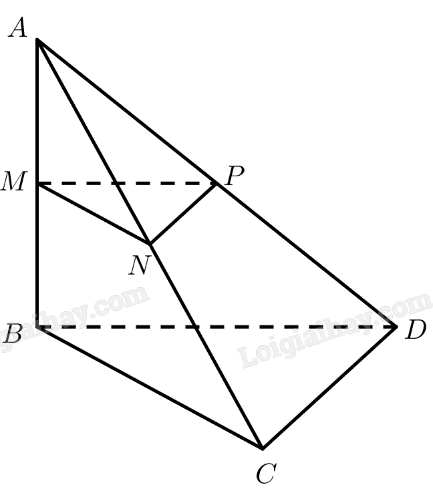
a) \(M\) là trung điểm của \(AB\)

\(N\) là trung điểm của \(AC\)

\( \Rightarrow MN\) là đường trung bình của tam giác \(ABC\)

\( \Rightarrow MN\parallel BC\)

\(AB \bot BC \Rightarrow MB \bot BC \Rightarrow d\left( {MN,BC} \right) = MB = \frac{1}{2}AB = \frac{a}{2}\)

b) \(M\) là trung điểm của \(AB\)

\(P\) là trung điểm của \(A{\rm{D}}\)

\( \Rightarrow MP\) là đường trung bình của tam giác \(ABD\)

\(\left. \begin{array}{l} \Rightarrow MP\parallel BD\\B{\rm{D}} \subset \left( {BC{\rm{D}}} \right)\end{array} \right\} \Rightarrow MP\parallel \left( {BC{\rm{D}}} \right)\)

\(AB \bot \left( {BCD} \right) \Rightarrow MB \bot \left( {BCD} \right) \Rightarrow d\left( {MP,\left( {BCD} \right)} \right) = d\left( {M,\left( {BCD} \right)} \right) = MB = \frac{a}{2}\)

\(\left. \begin{array}{l}\left. \begin{array}{l} \Rightarrow MN\parallel BC\\B{\rm{C}} \subset \left( {BC{\rm{D}}} \right)\end{array} \right\} \Rightarrow MN\parallel \left( {BC{\rm{D}}} \right)\\MP\parallel \left( {BC{\rm{D}}} \right)\\MN,MP \subset \left( {MNP} \right)\end{array} \right\} \Rightarrow \left( {MNP} \right)\parallel \left( {BC{\rm{D}}} \right)\)

\( \Rightarrow d\left( {\left( {MNP} \right),\left( {BCD} \right)} \right) = d\left( {M,\left( {BCD} \right)} \right) = MB = \frac{a}{2}\)

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Bài 4 trang 106 SGK Toán 11 tập 2 - Cánh Diều
Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\), đáy \(ABCD\) là hình vuông cạnh \(a\), \(SA = a\) (Hình 78).
Bài 5 trang 106 SGK Toán 11 tập 2 - Cánh Diều
Với giả thiết ở Bài tập 4, hãy:
Bài 2 trang 106 SGK Toán 11 tập 2 - Cánh Diều
Cho hình tứ diện \(ABCD\) có \(AB = a,BC = b,BD = c\),\(\widehat {ABC} = \widehat {ABD} = \widehat {BCD} = {90^ \circ }\). Gọi \(M,N,P\) lần lượt là trung điểm của \(AB,AC,AD\) (Hình 77).
Bài 1 trang 106 SGK Toán 11 tập 2 - Cánh Diều
Hình 76 gợi nên hình ảnh hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) song song với nhau.
Giải mục 6 trang 10, 105, 106 SGK Toán 11 tập 2 - Cánh Diều
Trong Hình 73, khuôn cửa phía trên và mép cánh cửa phía dưới gợi nên hình ảnh hai đường thẳng \(a\)
Giải mục 5 trang 103, 104 SGK Toán 11 tập 2 - Cánh Diều
a) Trong Hình 70, sàn nhà và trần nhà của căn phòng gợi nên hình ảnh hai mặt phẳng song song \(\left( P \right),\left( Q \right)\).
Giải mục 4 trang 102, 103 SGK Toán 11 tập 2 - Cánh Diều
Trong Hình 67, thanh gỗ dọc phía trên các cột và mặt đường hành lang gợi nên hình ảnh đường thẳng \(\Delta \) và mặt phẳng \(\left( P \right)\)
Giải mục 3 trang 102 SGK Toán 11 tập 2 - Cánh Diều
Trong Hình 64, hai mép của con đường gợi nên hình ảnh hai đường thẳng song song (Delta ) và (Delta '). Xét điểm (A) trên đường thẳng (Delta ).
Giải mục 2 trang 100, 101 SGK Toán 11 tập 2 - Cánh Diều
Khi lắp thiết bị cho nhà bạn Nam, bác thợ khoan tường tại vị trí (M)
Lý thuyết Khoảng cách - Toán 11 Cánh diều
1. Khoảng cách từ một điểm đến một đường thẳng Cho đường thẳng \(\Delta \) và điểm \(M\) không thuộc \(\Delta \).

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Cánh diều - Xem ngay

Báo lỗi - Góp ý

2K7 tham gia ngay group để nhận thông tin thi cử, tài liệu miễn phí, trao đổi học tập nhé!

>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.