Bài 5. Phương trình đường tròn Toán 10 Cánh diều

Lý thuyết Phương trình đường tròn - SGK Toán 10 Cánh diều

A. Lý thuyết 1. Phương trình đường tròn a) Phương trình đường tròn Điểm M(x;y) nằm trên đường tròn (C) khi và chỉ khi

Tổng hợp đề thi học kì 1 lớp 10 tất cả các môn - Cánh diều

Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...

A. Lý thuyết

1. Phương trình đường tròn

a) Phương trình đường tròn

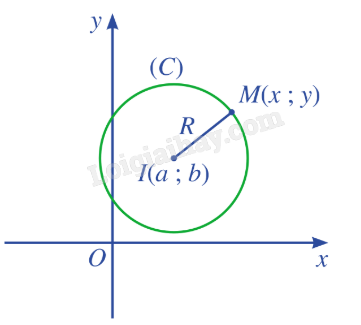
Điểm M(x;y) nằm trên đường tròn (C) khi và chỉ khi

\(IM = R \Leftrightarrow I{M^2} = {R^2} \Leftrightarrow {(x - a)^2} + {(y - b)^2} = {R^2}\).

Phương trình đường tròn tâm I(a;b) bán kính R là

\({(x - a)^2} + {(y - b)^2} = {R^2}\).

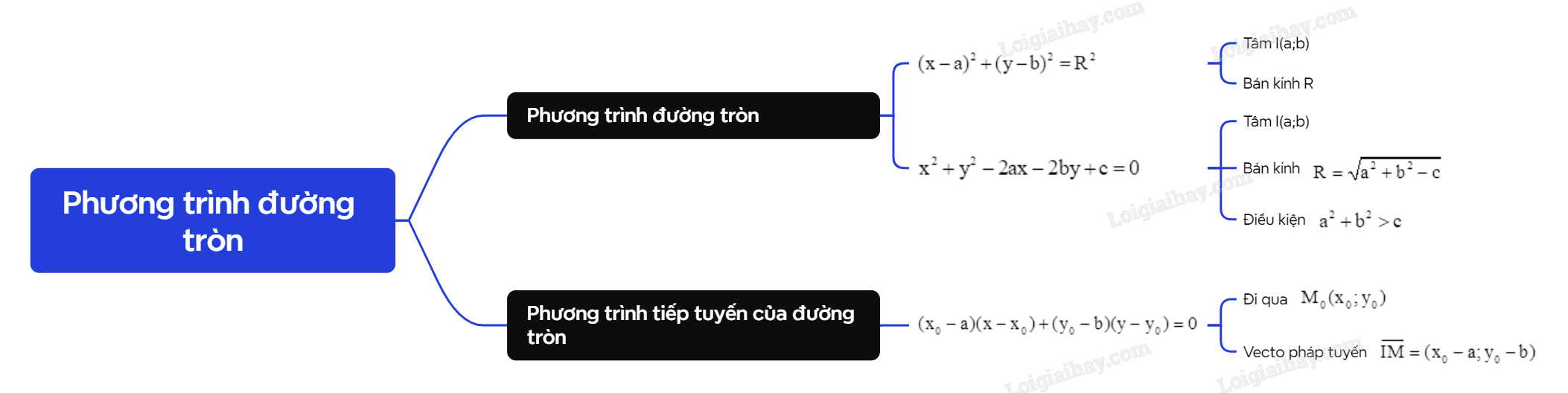
Phương trình đường tròn có thể viết ở dạng \({(x - a)^2} + {(y - b)^2} = {R^2}\) (chính tắc) hoặc đưa về dạng \({x^2} + {y^2} - 2ax - 2by + c = 0\) (tổng quát).

Nhận xét: Phương trình \({x^2} + {y^2} - 2ax - 2by + c = 0\) là phương trình của một đường tròn (C) khi và chỉ khi \({a^2} + {b^2} > c\). Khi đó, (C) có tâm I(a;b) và bán kính \(R = \sqrt {{a^2} + {b^2} - c} \).

b) Phương trình đường tròn đi qua ba điểm không thẳng hàng

Do có duy nhất một đường tròn đi qua ba điểm không thẳng hàng cho trước nên ta có thể lập được phương trình đường tròn đó khi biết tọa độ của ba điểm nói trên.

2. Phương trình tiếp tuyến của đường tròn

Cho đường tròn (C) tâm I(a;b) và điểm \({M_0}({x_0};{y_0})\) nằm trên đường tròn đó. Gọi \(\Delta \) là tiếp tuyến của (C) tại điểm \({M_0}({x_0};{y_0})\). Khi đó:

Đường thẳng \(\Delta \) đi qua điểm \({M_0}({x_0};{y_0})\) và có vecto pháp tuyến

\(\overrightarrow {IM} = ({x_0} - a;{y_0} - b)\).

Phương trình tiếp tuyến \(\Delta \) là

\(({x_0} - a)(x - {x_0}) + ({y_0} - b)(y - {y_0}) = 0\).

B. Bài tập

Bài 1:

a) Tìm tâm và bán kính đường tròn (C) có phương trình: \({(x - 2)^2} + {(y + 3)^2} = 16\).

b) Viết phương trình đường tròn (C’) tâm J(2;-1) và có bán kính gấp đôi bán kính đường tròn (C).

Giải:

a) Ta viết phương trình của (C) ở dạng \({(x - 2)^2} + {(y - ( - 3))^2} = {4^2}\).

Vậy (C) có tâm I(2;-3) và bán kính R = 4.

b) Đường tròn (C’) có tâm J(2;-1) và bán kính R’ = 2R = 8 nên có phương trình:

\({(x - 2)^2} + {(y + 1)^2} = 64\).

Bài 2: Phương trình \({x^2} + {y^2} - 4x + 2y - 4 = 0\) có phải là phương trình đường tròn không? Nếu có, xác định tọa độ tâm và bán kính của đường tròn đó.

Giải:

Từ phương trình, ta có \(a = \frac{{ - 4}}{{ - 2}} = 2\); \(b = \frac{2}{{ - 2}} = - 1\); c = -4.

Suy ra \({a^2} + {b^2} - c = {2^2} + {( - 1)^2} - ( - 4) = 9 > 0\).

Vậy phương trình \({x^2} + {y^2} - 4x + 2y - 4 = 0\) là phương trình đường tròn tâm I(2;-1) và bán kính \(R = \sqrt 9 = 3\).

Bài 3: Lập phương trình đường tròn đi qua ba điểm A(-1;1), B(0;-2), C(0;2).

Giải:

Giả sử tâm của đường tròn là điểm I(a;b). Ta có \(IA = IB = IC \Leftrightarrow I{A^2} = I{B^2} = I{C^2}\).

Khi đó:

\(\left\{ \begin{array}{l}{( - 1 - a)^2} + {(1 - b)^2} = {(0 - a)^2} + {( - 2 - b)^2}\\{(0 - a)^2} + {( - 2 - b)^2} = {(0 - a)^2} + {(2 - b)^2}\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}{a^2} + {b^2} + 2a - 2b + 2 = {a^2} + {b^2} + 4b + 4\\{a^2} + {b^2} + 4b + 4 = {a^2} + {b^2} - 4b + 4\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}2a - 2b = 4b + 2\\b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 0\end{array} \right.\).

Đường tròn tâm I(1;0) bán kính \(R = IC = \sqrt {{a^2} + {b^2} - 4b + 4} = \sqrt 5 \).

Phương trình đường tròn là \({(x - 1)^2} + {(y - 0)^2} = {(\sqrt 5 )^2}\).

Vậy phương trình đường tròn là \({(x - 1)^2} + {y^2} = 5\).

Bài 4: Cho đường tròn (C) có phương trình \({(x + 1)^2} + {(y - 3)^2} = 5\). Điểm M(0;1) có thuộc đường tròn (C) hay không? Nếu có, hãy viết phương trình tiếp tuyến tại M của (C).

Giải:

Do \({(0 + 1)^2} + {(1 - 3)^2} = 5\), nên điểm M thuộc (C).

Đường tròn (C) có tâm là I(-1;3). Tiếp tuyến của (C) tại M(0;1) có vecto pháp tuyến \( - 1(x - 0) + 2(y - 1) = 0 \Leftrightarrow x - 2y + 2 = 0\).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải mục I trang 87, 88, 89 SGK Toán 10 tập 2 - Cánh diều
a) Tính khoảng cách từ gốc toạ độ C(0;0) đến điểm M(3 ; 4) trong mặt phẳng toạ độ Oxy. Trong mặt phẳng toạ độ Oxy, nêu mối liên hệ giữa x và y để: Viết phương trình đường tròn tâm I(6 ; - 4) đi qua điểm A(8 ; – 7). Lập phương trình đường tròn đi qua ba điểm A(1; 2), B(5; 2), C(1 ; – 3).
Giải mục II trang 90 SGK Toán 10 tập 2 - Cánh diều
Lập phương trình tiếp tuyến tại điểm
Giải bài 1 trang 91 SGK Toán 10 tập 2 – Cánh diều
Phương trình nào sau đây là phương trình đường tròn ?
Giải bài 2 trang 91 SGK Toán 10 tập 2 – Cánh diều
Tìm tâm và bán kính của đường tròn trong môi trường hợp sau:
Giải bài 3 trang 91 SGK Toán 10 tập 2 – Cánh diều
Lập phương trình đường tròn trong mỗi trường hợp sau: a) Đường tròn có tâm I(- 3 ; 4) bán kính R = 9; b) Đường tròn có tâm I(5 ;-2) và đi qua điểm M(4;- 1); c) Đường tròn có tâm I(1;- 1) và có một tiếp tuyến là A: 5x- 12y – 1 = 0; d) Đường tròn đường kính AB với A(3;-4) và B(-1; 6); e) Đường tròn đi qua ba điểm A(1;1), B(3; 1), C(0; 4).
Giải bài 4 trang 92 SGK Toán 10 tập 2 – Cánh diều
Lập phương trình tiếp tuyến tại điểm có hoành độ bằng 3 thuộc đường tròn
Giải bài 5 trang 92 SGK Toán 10 tập 2 – Cánh diều
Tìm m sao cho đường thẳng 3x + 4y + m = 0 tiếp xúc với đường tròn
Giải bài 6 trang 92 SGK Toán 10 tập 2 – Cánh diều
Hình 46 mô phỏng một trạm thu phát sóng điện thoại di động đặt ở vị trí 1 có toạ độ (- 2 ; 1) trong mặt phẳng toạ độ (đơn vị trên hai trục là ki-lô-mét).
Giải bài 7 trang 92 SGK Toán 10 tập 2 – Cánh diều
Ném đĩa là một môn thể thao thi đấu trong Thế vận hội Olympic mùa hè. Khi thực hiện cú ném, vận động viên thường quay lưng lại với hướng ném, sau đó xoay ngược chiều kim đồng hồ một vòng rưỡi của đường tròn để lấy đà rồi thả tay ra khỏi đĩa