Lý thuyết Biểu thức tọa độ của các phép toán vecto - SGK Toán 10 Cánh diều
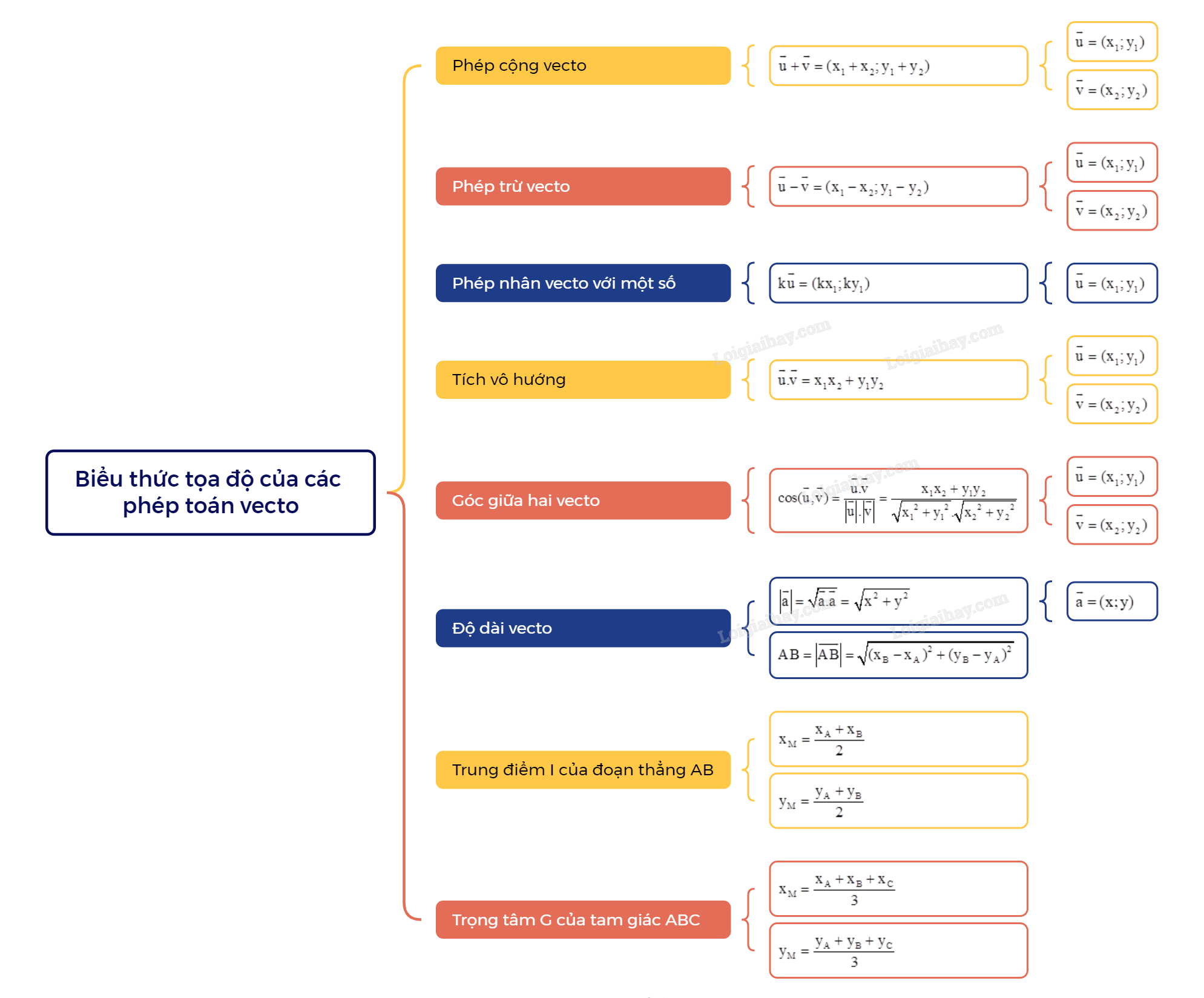
A. Lý thuyết 1. Biểu thức tọa độ của phép cộng hai vecto, phép trừ hai vecto, phép nhân một số với một vecto
A. Lý thuyết
1. Biểu thức tọa độ của phép cộng hai vecto, phép trừ hai vecto, phép nhân một số với một vecto
|
Nếu \(\overrightarrow u = ({x_1};{y_1})\) và \(\overrightarrow v = ({x_2};{y_2})\) thì: + \(\overrightarrow u + \overrightarrow v = ({x_1} + {x_2};{y_1} + {y_2})\). + \(\overrightarrow u - \overrightarrow v = ({x_1} - {x_2};{y_1} - {y_2})\). + \(k\overrightarrow u = (k{x_1};k{y_1})\) với \(k \in \mathbb{R}\). |
Nhận xét: Hai vecto \(\overrightarrow u = ({x_1};{y_1})\) và \(\overrightarrow v = ({x_2};{y_2})\) \((\overrightarrow v \ne \overrightarrow 0 )\) cùng phương khi và chỉ khi có một số thực k sao cho \({x_1} = k{x_2}\) và \({y_1} = k{y_2}\).
2. Tọa độ trung điểm đoạn thẳng và tọa độ trọng tâm tam giác
a) Tọa độ trung điểm đoạn thẳng
| Cho hai điểm \(A({x_A};{y_A})\) và \(B({x_B};{y_B})\). Nếu \(M({x_M};{y_M})\) là trung điểm đoạn thẳng AB thì \({x_M} = \frac{{{x_A} + {x_B}}}{2}\); \({y_M} = \frac{{{y_A} + {y_B}}}{2}\). |
b) Tọa độ trọng tâm tam giác
| Cho tam giác ABC có \(A({x_A};{y_A})\), \(B({x_B};{y_B})\), \(C({x_C};{y_C})\). Nếu \(G({x_G};{y_G})\) là trọng tâm tam giác ABC thì \({x_M} = \frac{{{x_A} + {x_B} + {x_C}}}{3}\); \({y_M} = \frac{{{y_A} + {y_B} + {y_C}}}{3}\). |
3. Biểu thức tọa độ của tích vô hướng
| Nếu \(\overrightarrow u = ({x_1};{y_1})\) và \(\overrightarrow v = ({x_2};{y_2})\) thì \(\overrightarrow u .\overrightarrow v = {x_1}{x_2} + {y_1}{y_2}\). |
Nhận xét:
a) Nếu \(\overrightarrow a = (x;y)\) thì \(\left| {\overrightarrow a } \right| = \sqrt {\overrightarrow a .\overrightarrow a } = \sqrt {{x^2} + {y^2}} \).
b) Nếu \(A({x_A};{y_A})\) và \(B({x_B};{y_B})\) thì \(AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{{({x_B} - {x_A})}^2} + {{({y_B} - {y_A})}^2}} \).
c) Với hai vecto \(\overrightarrow u = ({x_1};{y_1})\) và \(\overrightarrow v = ({x_2};{y_2})\) đều khác \(\overrightarrow 0 \), ta có:
+ \(\overrightarrow u \) vuông góc \(\overrightarrow v \) khi và chỉ khi \(\overrightarrow u .\overrightarrow v = {x_1}{x_2} + {y_1}{y_2} = 0\).
+ \(\cos (\overrightarrow u ,\overrightarrow v ) = \frac{{\overrightarrow u .\overrightarrow v }}{{\left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|}} = \frac{{{x_1}{x_2} + {y_1}{y_2}}}{{\sqrt {{x_1}^2 + {y_1}^2} .\sqrt {{x_2}^2 + {y_2}^2} }}\).
B. Bài tập
Bài 1: Cho \(\overrightarrow u = (2; - 1)\), \(\overrightarrow v = (1;5)\). Tìm tọa độ của \(\overrightarrow u + \overrightarrow v \) và \(\overrightarrow u - \overrightarrow v \).
Giải:
\(\overrightarrow u + \overrightarrow v = (2 + 1; - 1 + 5) = (3;4)\);
\(\overrightarrow u - \overrightarrow v = (2 - 1; - 1 - 5) = (1; - 6)\).
Bài 2: Cho ba điểm A(-1;-3), B(2;3) và C(3;5). Chứng minh ba điểm A, B, C thẳng hàng.
Giải:
Ta có: \(\overrightarrow {AB} = (3;6)\), \(\overrightarrow {BC} = (1;2)\). Suy ra \(\overrightarrow {AB} = 3\overrightarrow {BC} \).
Vậy ba điểm A, B, C thẳng hàng.
Bài 3: Cho tam giác ABC có A(-2; 1), B(2; 5), C(5; 2). Tìm tọa độ trung điểm M của đoạn thẳng AB và trọng tâm G của tam giác ABC.
Giải:
Do \(M({x_M};{y_M})\) là trung điểm của đoạn thẳng AB nên:
\({x_M} = \frac{{ - 2 + 2}}{2} = 0\); \({y_M} = \frac{{1 + 5}}{2} = 3\).
Vậy M(0; 3).
Do \(G({x_G};{y_G})\) là trọng tâm tam giác ABC nên:
\({x_G} = \frac{{ - 2 + 2 + 5}}{3} = \frac{5}{3}\);
\({y_G} = \frac{{1 + 5 + 2}}{3} = \frac{8}{3}\).
Vậy \(G\left( {\frac{5}{3};\frac{8}{3}} \right)\).
Bài 4: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(2; 2), B(1; -1), C(8; 0).
a) Tính \(\overrightarrow {BA} .\overrightarrow {BC} \) và \(\cos \widehat {ABC}\).
b) Chứng minh \(\overrightarrow {AB} \bot \overrightarrow {AC} \).
c) Giải tam giác ABC.
Giải:
a) Ta có \(\overrightarrow {BA} = (1;3)\), \(\overrightarrow {BC} = (7;1)\).
Do đó \(\overrightarrow {BA} .\overrightarrow {BC} = 1.7 + 3.1 = 10\).
Mặt khác: \(\left| {\overrightarrow {BA} } \right| = \sqrt {{1^2} + {3^2}} = \sqrt {10} \), \(\left| {\overrightarrow {BC} } \right| = \sqrt {{7^2} + {1^2}} = \sqrt {50} \).
\(\cos \widehat {ABC} = \cos (\overrightarrow {BA} ,\overrightarrow {BC} ) = \frac{{\overrightarrow {BA} .\overrightarrow {BC} }}{{\left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|}} = \frac{{10}}{{\sqrt {10} .\sqrt {50} }} = \frac{{\sqrt 5 }}{5}\).
b) Có \(\overrightarrow {AB} = ( - 1; - 3)\) và \(\overrightarrow {AC} = (6; - 2)\) nên:
\(\overrightarrow {AB} .\overrightarrow {AC} = ( - 1).6 + ( - 3).( - 2) = 0\).
Vậy \(\overrightarrow {AB} \bot \overrightarrow {AC} \).
c) Do \(\overrightarrow {AB} \bot \overrightarrow {AC} \) nên \(\widehat {BAC} = {90^o}\), tức tam giác ABC vuông tại A.
Mà \(\cos \widehat {ABC} = \frac{{\sqrt 5 }}{5}\) nên \(\widehat {ABC} \approx {63^o}\). Vì vậy \(\widehat {ACB} \approx {90^o} - {63^o} = {27^o}\).
Mặt khác: \(AB = \left| {\overrightarrow {BA} } \right| = \sqrt {10} \), \(BC = \left| {\overrightarrow {BC} } \right| = \sqrt {50} = 5\sqrt 2 \),
\(CA = \sqrt {B{C^2} - A{B^2}} = \sqrt {{{\left( {5\sqrt 2 } \right)}^2} - {{\left( {\sqrt {10} } \right)}^2}} = 2\sqrt {10} \).
Các bài khác cùng chuyên mục
- Lý thuyết Ba đường conic - SGK Toán 10 Cánh diều
- Lý thuyết Phương trình đường tròn - SGK Toán 10 Cánh diều
- Lý thuyết Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng - SGK Toán 10 Cánh diều
- Lý thuyết Phương trình đường thẳng - SGK Toán 10 Cánh diều
- Lý thuyết Biểu thức tọa độ của các phép toán vecto - SGK Toán 10 Cánh diều
- Lý thuyết Ba đường conic - SGK Toán 10 Cánh diều
- Lý thuyết Phương trình đường tròn - SGK Toán 10 Cánh diều
- Lý thuyết Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng - SGK Toán 10 Cánh diều
- Lý thuyết Phương trình đường thẳng - SGK Toán 10 Cánh diều
- Lý thuyết Biểu thức tọa độ của các phép toán vecto - SGK Toán 10 Cánh diều













Danh sách bình luận