Toán 12 Cùng khám phá | Giải toán lớp 12 Cùng khám phá Bài 3. Hệ trục tọa độ trong không gian - Toán 12 Cùng k..

Lý thuyết Hệ trục tọa độ trong không gian Toán 12 Cùng khám phá


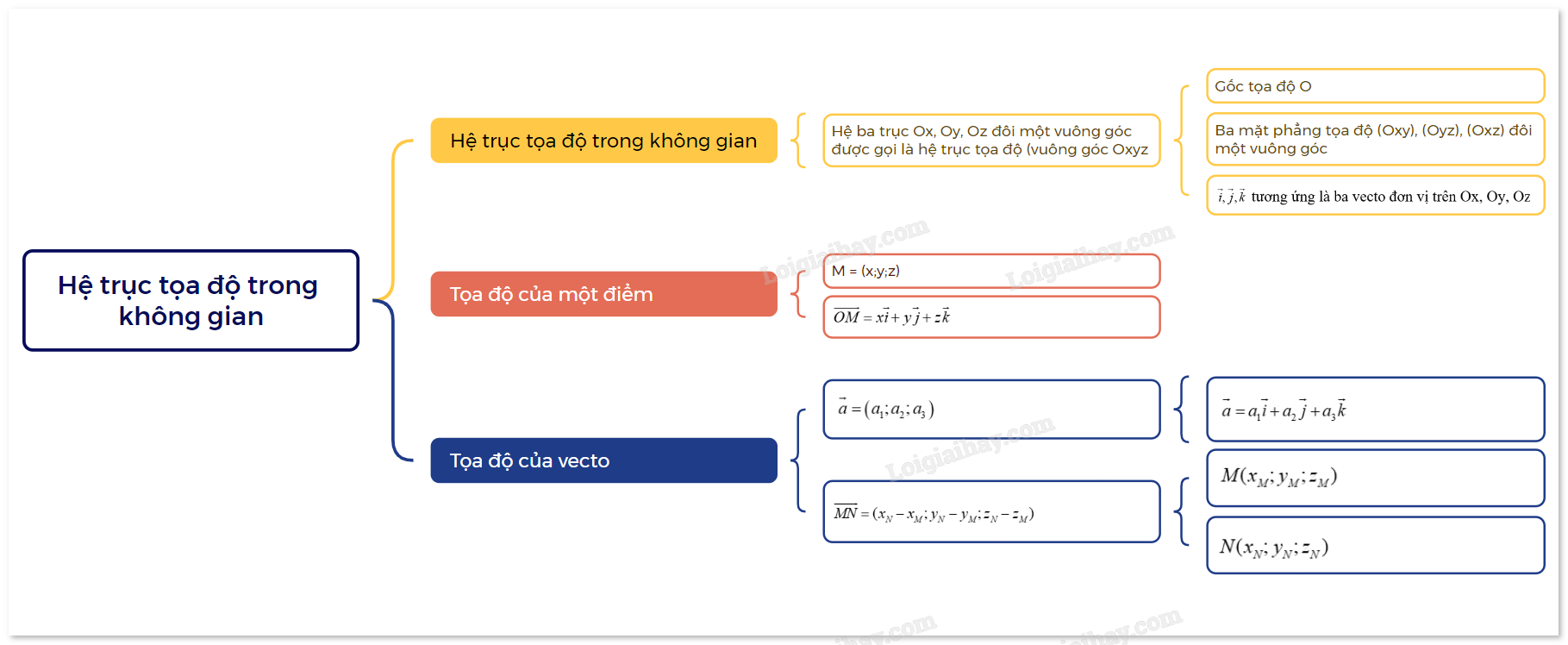
1. Hệ trục tọa độ trong không gian

1. Hệ trục tọa độ trong không gian

Trong không gian, hệ ba trục Ox, Oy, Oz đôi một vuông góc được gọi là hệ trục tọa độ vuông góc Oxyz, hay đơn giản gọi là hệ tọa độ Oxyz. 

Lưu ý:

- Điểm O được gọi là gốc tọa độ

- Ba trục Ox, Oy, Oz lần lượt được gọi là trục hoành, trục tung, trục cao

- Ba mặt phẳng (Oxy), (Oxz), (Oyz) đôi một vuông góc với nhau, được gọi là các mặt phẳng tọa độ. Không gian gắn với hệ tọa độ Oxyz được gọi là không gian Oxyz

- Ta quy ước gọi \(\overrightarrow i ,\overrightarrow j ,\overrightarrow k \) tương ứng là ba vecto đơn vị trên ba trục Ox, Oy, Oz. Từ nay trở đi, nếu không nói gì thêm thì ta hiểu Không gian Oxyz đã có bộ ba vecto đơn vị trên các trục là \(\overrightarrow i ,\overrightarrow j ,\overrightarrow k \). Vì các vecto \(\overrightarrow i ,\overrightarrow j ,\overrightarrow k \) có độ dài bằng 1 và đôi một vuông góc với nhau nên:

\({\overrightarrow i ^2} = {\overrightarrow j ^2} = {\overrightarrow k ^2} = 1\)

\(\overrightarrow i .\overrightarrow j  = \overrightarrow j .\overrightarrow k  = \overrightarrow k .\overrightarrow i  = 0\)

2. Tọa độ của một điểm

Trong không gian Oxyz, cho điểm M. Nếu \[\overrightarrow {OM}  = x\overrightarrow i  + y\overrightarrow j  + z\overrightarrow k \] thì ta gọi bộ ba số (x;y;z) là tọa độ điểm M đối với hệ trục tọa độ Oxyz và viết M = (x;y;z) hoặc M (x;y;z); x là hoành độ, y là tung độ, z là cao độ của điểm M.

3. Tọa độ của vecto

Trong không gian Oxyz, cho \(\overrightarrow a \). Nếu \[\overrightarrow a  = {a_1}\overrightarrow i  + {a_2}\overrightarrow j  + {a_3}\overrightarrow k \] thì ta gọi bộ ba số \(\left( {{a_1};{a_2};{a_3}} \right)\) là tọa độ của \(\overrightarrow a \) đối với hệ tọa độ Oxyz và viết \(\overrightarrow a  = \left( {{a_1};{a_2};{a_3}} \right)\) hoặc \(\overrightarrow a \left( {{a_1};{a_2};{a_3}} \right)\)

Trong không gian Oxyz, nếu \(M({x_M};{y_M};{z_M})\) và \(N({x_N};{y_N};{z_N})\) thì:

\(\overrightarrow {MN}  = ({x_N} - {x_M};{y_N} - {y_M};{z_N} - {z_M})\)

Ví dụ: Trong không gian Oxyz, cho hình lăng trụ tam giác ABC.A’B’C có A(1;0;2), B(3;2;5), C(7;-3;9).

Tìm tọa độ của \(\overrightarrow {AA'} \).

Tìm tọa độ của các điểm B’, C’.

Lời giải

Ta có: \(\overrightarrow {AA'}  = ({x_{A'}} - {x_A};{y_{A'}} - {y_A};{z_{A'}} - {z_A}) = (4;0; - 1)\).

Gọi tọa độ của điểm B’ là (x,y,z) thì \(\overrightarrow {BB'} \) = (x-3;y-2;z-5). Vì ABC.A’B’C’ là hình lăng trụ nên ABB’A’ là hình bình hành, suy ra \(\overrightarrow {AA'} \) = \(\overrightarrow {BB'} \).

Do đó \(\left\{ \begin{array}{l}x - 3 = 4\\y - 2 = 0\\z - 5 =  - 1\end{array} \right.\) hay x = 7, y = 2, z = 4. Vậy B’(7;2;4).

Lập luận tương tự suy ra C’(11;-3;8).


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo
  • Giải mục 1 trang 66, 67, 68 SGK Toán 12 tập 1 - Cùng khám phá

    Làm thế nào để định vị một đối tượng trong một nhà kho lớn? Bác Quản là thủ kho vật liệu của nhà máy. Trong kho có nhiều giá xếp hàng, được xếp song song với một bức tường như Hình 2.28. Nhà kho rất lớn nên để dễ dàng tìm các thùng hàng, bác dùng ba số để ghi chép vị trí của chúng theo quy ước: Số thứ nhất cho biết thùng hàng nằm ở giá nào (các giá được đánh số theo thứ tự từ trái sang phải, theo mũi tên ??); Số thứ hai cho biết thùng hàng nằm ở ngăn thứ mấy của giá (các ngăn của mỗi giá đượ

  • Giải mục 2 trang 68, 69, 70 SGK Toán 12 tập 1 - Cùng khám phá

    Cho điểm trong không gian Oxyz. Trong ba mặt phẳng tọa độ là ba lưới ô vuông có cạnh bằng đơn vị. Biết rằng , và vị trí các điểm M’, A, B, C được cho như trong Hình 2.32. a) Biếu diễn theo hai vecto và . b) Biểu diễn theo hai vecto đơn vị . c) Biểu diễn theo ba vectơ dơn vị .

  • Giải mục 3 trang 70, 71, 72 SGK Toán 12 tập 1 - Cùng khám phá

    Trong không gian Oxyz, cho vectơ (vec a). a) Xác định điểm M sao cho (overrightarrow {OM} = vec a). b) Gọi (left( {x;y;z} right)) là toạ độ của điểm M. Hãy biểu diễn (vec a) theo ba vectơ đơn vị (vec i,vec j,vec k).

  • Giải bài tập 2.13 trang 73 SGK Toán 12 tập 1 - Cùng khám phá

    Trong không gian Oxyz, cho hình hộp chữ nhật \(OABC \cdot {O^\prime }{A^\prime }{B^\prime }{C^\prime }\). Các đỉnh \(A,C,{O^\prime }\) tương ứng thuộc các tia Ox,Oy,Oz và \(OA = 3,OC = 4,O{O^\prime } = 2\). Tìm toạ độ của: a) Vectơ \(\overrightarrow {{O^\prime }B} \); b) Điểm \(G\), với \(G\) là trung điểm của đoạn thẳng \({O^\prime }B\).

  • Giải bài tập 2.14 trang 73 SGK Toán 12 tập 1 - Cùng khám phá

    Cho hình hộp đứng ABCD.A’B’C’D’ có đáy là hình thoi. Hai đường chéo AC, BD của đáy có chiểu dài lần lượt là a, b. Cạnh bên AA’ = c. Hệ toạ độ Oxyz có gốc trùng với giao điểm O của hai đường chéo hình thoi ABCD, có tia Ox trùng với tia OB và tia Oy trùng với tia OC (Hinh 2.39). Hãy xác định: a) Toạ độ các đỉnh của hình hộp; b) Toạ độ vectơ \(\overrightarrow {B{D^\prime }} \).

>> Xem thêm

Báo lỗi - Góp ý

Group Ôn Thi ĐGNL & ĐGTD Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store