Lý thuyết Giá trị lượng giác của một góc từ 0 đến 180

Tổng hợp đề thi giữa kì 1 lớp 10 tất cả các môn - Kết nối tri thức

Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...

1. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC

+) Nửa đường tròn đơn vị: nửa đường tròn tâm O, bán kính R = 1 nằm phía trên trục hoành (H.3.2).

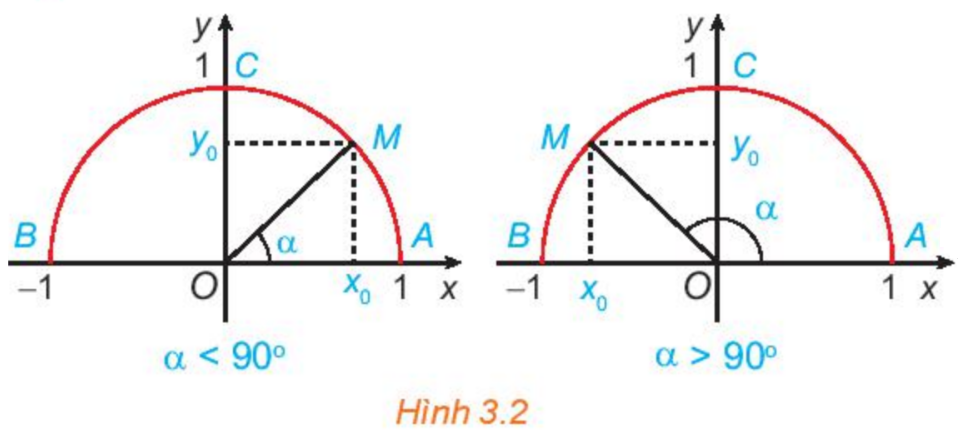
+) Với mỗi góc \(\alpha \) \(({0^o} \le \alpha \le {180^o})\) có duy nhất điểm \(M({x_0};{y_0})\) trên nửa đường tròn đơn vị nói trên để \(\widehat {xOM} = \alpha \). Khi đó:

\(\sin \alpha = {y_0}\) là tung độ của M;

\(\cos \alpha = {x_0}\) là hoành độ của M;

\(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{{y_0}}}{{{x_0}}}(\alpha \ne {90^o})\);

\(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{{{x_0}}}{{{y_0}}}(\alpha \ne {0^o},\alpha \ne {180^o})\).

+) Bảng giá trị lượng giác của một số góc đặc biệt:

+) Tìm các giá trị lượng giác của góc bằng máy tính cầm tay.

Trước tiên, bấm phím SHIFT MODE rồi bấm phím 3 để chọn đơn vị góc là “độ”.

Chú ý:

Khi tìm x biết sinx, máy tính chỉ đưa ra giá trị \(x \le {90^o}\).

Để tính cotx, ta tính 1: tanx.

2. MỐI QUAN HỆ GIỮA CÁC GIÁ TRỊ LƯỢNG GIÁC CỦA HAI GÓC BÙ NHAU

* Hai góc bù nhau, \(\alpha \) và \({180^o} - \alpha \):

\(\begin{array}{l}\sin \left( {{{180}^o} - \alpha } \right) = \sin \alpha \\\cos \left( {{{180}^o} - \alpha } \right) = - \cos \alpha \\\tan \left( {{{180}^o} - \alpha } \right) = - \tan \alpha (\alpha \ne {90^o})\\\cot \left( {{{180}^o} - \alpha } \right) = - \cot \alpha ({0^o} < \alpha < {180^o})\end{array}\)

* Hai góc phụ nhau, \(\alpha \) và \({90^o} - \alpha \):

\(\begin{array}{l}\sin \left( {{{90}^o} - \alpha } \right) = \cos \alpha \\\cos \left( {{{90}^o} - \alpha } \right) = \sin \alpha \\\tan \left( {{{90}^o} - \alpha } \right) = \cot \alpha (\alpha \ne {90^o},{0^o} < \alpha < {180^o})\\\cot \left( {{{90}^o} - \alpha } \right) = \tan \alpha (\alpha \ne {90^o},{0^o} < \alpha < {180^o})\end{array}\)

👉

Giải bài nhanh với AI Hay:

Bình luận

Chia sẻ

Bình chọn:

4.7 trên 10 phiếu

Bài tiếp theo

Giải câu hỏi mở đầu trang 33 SGK Toán 10 tập 1 - Kết nối tri thức
Bạn đã biết tỉ số lượng giác của một góc nhọn. Đối với góc tù thì sao?
Giải mục 1 trang 34, 35 SGK Toán 10 tập 1 - Kết nối tri thức
a) Nêu nhận xét về vị trí điểm M trên nửa đường tròn đơn vị trong mỗi trường hợp sau: Tìm các giá trị lượng giác của góc 120
Giải mục 2 trang 36, 37 SGK Toán 10 tập 1 - Kết nối tri thức
Nêu nhận xét về vị trí của hai điểm M, M’ đối với trục Oy. Từ đó nêu các mối quan hệ giữa Trong Hình 3.6, hai điểm M, N ứng với hai góc phụ nhau Một chiếc đu quay có bán kính 75 m, tâm của vòng quay ở độ cao 90 m (H.3.7), thời gian thực hiện mỗi vòng quay của đu quay là 30 phút. Nếu một người vào cabin tại vị trí thấp nhất của vòng quay, thì sau 20 phút quay, người đó ở độ cao bao nhiêu mét?
Giải bài 3.1 trang 37 SGK Toán 10 tập 1 – Kết nối tri thức
Không dùng bảng số hay máy tính cầm tay, tính giá trị của các biểu thức sau:
Giải bài 3.2 trang 37 SGK Toán 10 tập 1 – Kết nối tri thức
Đơn giản các biểu thức sau:
Giải bài 3.3 trang 37 SGK Toán 10 tập 1 – Kết nối tri thức
Chứng minh các hệ thức sau:
Giải bài 3.4 trang 37 SGK Toán 10 tập 1 – Kết nối tri thức
Cho góc thỏa mãn Tính giá trị biểu thức: