Giải mục 3 trang 69, 70, 71, 72, 73 SGK Toán 12 tập 2 - Cánh diều

HĐ6

Trả lời câu hỏi Hoạt động 6 trang 69 SGK Toán 12 Cánh diều

Cho hai đường thẳng \({\Delta _1},{\Delta _2}\) trong không gian có vectơ chỉ phương lần lượt là \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) . Giả sử \(\Delta _1',\Delta _2'\) là hai đường thẳng cùng đi qua điểm I và lần lượt song song (hoặc trùng) với \({\Delta _1},{\Delta _2}\) (Hình 28).

a) Nêu mối liên hệ giữa hai góc \(\left( {{\Delta _1},{\Delta _2}} \right)\) và \(\left( {{\Delta _1}',{\Delta _2}'} \right)\).

b) Gọi A và B là các điểm lần lượt thuộc hai đường thẳng \({\Delta _1}'\) và \({\Delta _2}'\) sao cho \(\overrightarrow {IA}  = \overrightarrow {{u_1}} ,\) \(\overrightarrow {IB}  = \overrightarrow {{u_2}} \) . So sánh \(\cos \left( {{\Delta _1}',{\Delta _2}'} \right),\left| {\cos \left( {\overrightarrow {IA} ,\overrightarrow {IB} } \right)} \right|,\left| {\cos \left( {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right)} \right|\).

c) So sánh \(\cos \left( {{\Delta _1},{\Delta _2}} \right),\frac{{\left| {\overrightarrow {{u_1}} .\overrightarrow {{u_2}} } \right|}}{{\left| {\overrightarrow {{u_1}} } \right|.\left| {\overrightarrow {{u_2}} } \right|}}\).

Phương pháp giải:

Sử dụng kiến thức về góc giữa hai đường thẳng để chứng minh: Góc giữa hai đường thẳng m và n trong không gian là góc giữa hai đường thẳng a và b cùng đi qua một điểm và tương ứng song song với m và n.

Lời giải chi tiết:

a) Vì \({\Delta _1}',{\Delta _2}'\) là hai đường thẳng cùng đi qua I và lần lượt song song (hoặc trùng) với \({\Delta _1},{\Delta _2}\) nên \(\left( {{\Delta _1},{\Delta _2}} \right) = \left( {{\Delta _1}',{\Delta _2}'} \right)\).

b) Ta có: \(\cos \left( {\Delta _1^',\Delta _2^'} \right) = \left| {\cos \left( {\overrightarrow {IA} ,\overrightarrow {IB} } \right)} \right| = \frac{{\left| {\overrightarrow {IA} .\overrightarrow {IB} } \right|}}{{\left| {\overrightarrow {IA} } \right|\left| {\overrightarrow {IB} } \right|}} = \frac{{\left| {\overrightarrow {{u_1}} .\overrightarrow {{u_2}} } \right|}}{{\left| {\overrightarrow {{u_1}} } \right|.\left| {\overrightarrow {{u_2}} } \right|}} = \left| {\cos \left( {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right)} \right|\).

Vậy \(\cos \left( {{\Delta _1}',{\Delta _2}'} \right) = \left| {\cos \left( {\overrightarrow {IA} ,\overrightarrow {IB} } \right)} \right| = \left| {\cos \left( {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right)} \right|\).

c) Ta có \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \cos \left( {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right) = \frac{{\left| {\overrightarrow {{u_1}} .\overrightarrow {{u_2}} } \right|}}{{\left| {\overrightarrow {{u_1}} } \right|.\left| {\overrightarrow {{u_2}} } \right|}}\).

LT6

Trả lời câu hỏi Luyện tập 6 trang 70 SGK Toán 12 Cánh diều

Cho đường thẳng \(\Delta :\frac{x}{2} = \frac{y}{{ - 1}} = \frac{z}{2}\). Tính côsin của góc giữa đường thẳng \(\Delta \) và các trục tọa độ.

Phương pháp giải:

Sử dụng kiến thức về côsin góc giữa hai đường thẳng để tính: Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) có vectơ chỉ phương lần lượt là \(\overrightarrow {{u_1}}  = \left( {{a_1};{b_1};{c_1}} \right)\), \(\overrightarrow {{u_2}}  = \left( {{a_2};{b_2};{c_2}} \right)\). Khi đó, ta có: \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2} + {c_1}{c_2}} \right|}}{{\sqrt {a_1^2 + b_1^2 + c_1^2} .\sqrt {a_2^2 + b_2^2 + c_2^2} }}\).

Lời giải chi tiết:

Trục Ox có một vectơ chỉ phương là \(\overrightarrow i  = \left( {1;0;0} \right)\), trục Oy có một vectơ chỉ phương là \(\overrightarrow j  = \left( {0;1;0} \right)\), trục Oz có một vectơ chỉ phương là \(\overrightarrow k  = \left( {0;0;1} \right)\), đường thẳng \(\Delta \) có một vectơ chỉ phương là \(\left( {2; - 1;2} \right)\).

Do đó, \(\cos \left( {\Delta ,Ox} \right) = \frac{{\left| {2.1 - 1.0 + 2.0} \right|}}{{\sqrt {{2^2} + {{\left( { - 1} \right)}^2} + {2^2}} .\sqrt {{1^2} + {0^2} + {0^2}} }} = \frac{2}{3}\);

\(\cos \left( {\Delta ,Oy} \right) = \frac{{\left| {2.0 - 1.1 + 2.0} \right|}}{{\sqrt {{2^2} + {{\left( { - 1} \right)}^2} + {2^2}} .\sqrt {{0^2} + {1^2} + {0^2}} }} = \frac{1}{3}\);

\(\cos \left( {\Delta ,Oz} \right) = \frac{{\left| {2.0 - 1.0 + 2.1} \right|}}{{\sqrt {{2^2} + {{\left( { - 1} \right)}^2} + {2^2}} .\sqrt {{0^2} + {0^2} + {1^2}} }} = \frac{2}{3}\).

HĐ7

Trả lời câu hỏi Hoạt động 7 trang 71 SGK Toán 12 Cánh diều

Cho mặt phẳng (P) có vectơ pháp tuyến là \(\overrightarrow n \), đường thẳng \(\Delta \) có vectơ chỉ phương là \(\overrightarrow u \) và đường thẳng \(\Delta \) cắt mặt phẳng (P) tại I. Gọi \(\Delta '\) là hình chiếu của \(\Delta \) trên mặt phẳng (P) (Hình 29).

a) Hãy xác định góc giữa đường thẳng \(\Delta \) và mặt phẳng (P).

b) So sánh \(\sin \left( {\Delta ,\left( P \right)} \right)\) và \(\left| {\cos \left( {\overrightarrow u ,\overrightarrow n } \right)} \right|\).

Phương pháp giải:

Sử dụng kiến thức về góc giữa đường thẳng và mặt phẳng để tìm góc giữa đường thẳng \(\Delta \) và mặt phẳng (P): Góc giữa đường thẳng d và mặt phẳng (P) là góc giữa đường thẳng d và hình chiếu của d trên mặt phẳng (P).

Lời giải chi tiết:

a) Vì \(\Delta '\) là hình chiếu của \(\Delta \) trên mặt phẳng (P) nên góc giữa đường thẳng \(\Delta \) và mặt phẳng (P) bằng góc giữa đường thẳng \(\Delta '\) và đường thẳng \(\Delta \).

b) Ta có \(\sin \left( {\Delta ,\left( P \right)} \right) = \sin \left( {\Delta ,\Delta '} \right) = \left| {\cos \left( {\overrightarrow u ,\overrightarrow n } \right)} \right|\).

LT7

Trả lời câu hỏi Luyện tập 6 trang 71 SGK Toán 12 Cánh diều

Cho mặt phẳng (P) có vectơ pháp tuyến \(\overrightarrow n  = \left( {A;B;C} \right)\). Tính sin của góc giữa mặt phẳng (P) và các trục tọa độ.

Phương pháp giải:

Sử dụng kiến thức về côsin góc giữa đường thẳng và mặt phẳng để tính: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng \(\Delta \) có vectơ chỉ phương \(\overrightarrow u  = \left( {{a_1};{b_1};{c_1}} \right)\) và mặt phẳng (P) có vectơ pháp tuyến \(\overrightarrow n  = \left( {{a_2};{b_2};{c_2}} \right)\). Gọi \(\left( {\Delta ,\left( P \right)} \right)\) là góc giữa đường thẳng \(\Delta \) và mặt phẳng (P). Khi đó, \(\sin \left( {\Delta ,\left( P \right)} \right) = \left| {\cos \left( {\overrightarrow u ,\overrightarrow n } \right)} \right| = \frac{{\left| {\overrightarrow u .\overrightarrow n } \right|}}{{\left| {\overrightarrow u } \right|.\left| {\overrightarrow n } \right|}} = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2} + {c_1}{c_2}} \right|}}{{\sqrt {a_1^2 + b_1^2 + c_1^2} .\sqrt {a_2^2 + b_2^2 + c_2^2} }}\).

Lời giải chi tiết:

Trục Ox có một vectơ chỉ phương là \(\overrightarrow i  = \left( {1;0;0} \right)\), trục Oy có một vectơ chỉ phương là \(\overrightarrow j  = \left( {0;1;0} \right)\), trục Oz có một vectơ chỉ phương là \(\overrightarrow k  = \left( {0;0;1} \right)\), mặt phẳng (P) có một vectơ pháp tuyến là \(\overrightarrow n  = \left( {A;B;C} \right)\).

Do đó, \(\sin \left( {\left( P \right),Ox} \right) = \frac{{\left| {A.1 + B.0 + C.0} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} .\sqrt {{1^2} + {0^2} + {0^2}} }} = \frac{{\left| A \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\);

\(\sin \left( {\left( P \right),Oy} \right) = \frac{{\left| {A.0 + B.1 + C.0} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} .\sqrt {{0^2} + {1^2} + {0^2}} }} = \frac{{\left| B \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\);

\(\sin \left( {\left( P \right),Oz} \right) = \frac{{\left| {A.0 + B.0 + C.1} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} .\sqrt {{0^2} + {0^2} + {1^2}} }} = \frac{{\left| C \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\).

HĐ8

Trả lời câu hỏi Hoạt động 8 trang 72 SGK Toán 12 Cánh diều

Cho hai mặt phẳng \(\left( {{P_1}} \right)\) và \(\left( {{P_2}} \right)\). Lấy hai đường thẳng \({\Delta _1},{\Delta _2}\) sao cho \({\Delta _1} \bot \left( {{P_1}} \right),\) \({\Delta _2} \bot \left( {{P_2}} \right)\) (Hình 31).

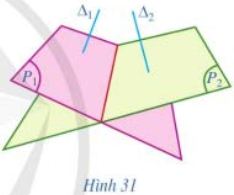
a) Nêu cách xác định góc giữa hai đường thẳng \({\Delta _1},{\Delta _2}\).

b) Góc đó có phụ thuộc vào việc chọn hai đường thẳng \({\Delta _1},{\Delta _2}\) như trên không?

Phương pháp giải:

Sử dụng kiến thức về góc giữa hai đường thẳng để tính: Góc giữa hai đường thẳng m và n trong không gian là góc giữa hai đường thẳng a và b cùng đi qua một điểm và tương ứng song song với m và n.

Lời giải chi tiết:

a) Vẽ hai đường thẳng \(\Delta _1',\Delta _2'\) cùng đi qua điểm I và lần lượt song song (hoặc trùng) với \({\Delta _1},{\Delta _2}\). Khi đó, góc giữa hai đường thẳng \({\Delta _1},{\Delta _2}\) là góc giữa hai đường thẳng \(\Delta _1',\Delta _2'\).

b) Vì \({\Delta _1} \bot \left( {{P_1}} \right)\) và \(\Delta _1'\) song song (hoặc trùng) với \({\Delta _1}\) nên \(\Delta _1' \bot \left( {{P_1}} \right)\).

Tương tự ta có: \(\Delta _2' \bot \left( {{P_2}} \right)\).

Khi đó, góc giữa hai đường thẳng \(\Delta _1',\Delta _2'\) luôn là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng \(\left( {{P_1}} \right)\) và \(\left( {{P_2}} \right)\) nên góc giữa hai đường thẳng \({\Delta _1},{\Delta _2}\) không phụ thuộc vào việc chọn hai đường thẳng \({\Delta _1},{\Delta _2}\).

LT8

Trả lời câu hỏi Luyện tập 8 trang 72 SGK Toán 12 Cánh diều

Trong Ví dụ 10, tính góc giữa hai mặt phẳng (BCC’B’) và (CDA’B’).

Phương pháp giải:

Sử dụng kiến thức về góc giữa hai mặt phẳng để tính góc giữa hai mặt phẳng: Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.

Lời giải chi tiết:

Vì ADD’A’ là hình vuông nên \(AD' \bot A'D\). Vì \(CD \bot \left( {ADD'A'} \right)\) nên \(CD \bot AD'\). Do đó, \(AD' \bot \left( {CDA'B'} \right)\).

Mặt khác, \(C'D' \bot \left( {BCC'B'} \right)\), suy ra góc giữa hai mặt phẳng (BCC’B’) và (CDA’B’) là góc giữa hai đường thẳng AD’ và C’D’, đó là góc AD’C’.

Vì \(C'D' \bot \left( {ADD'A'} \right)\) nên \(C'D' \bot AD'\), suy ra . Do đó, góc giữa hai mặt phẳng (BCC’B’) và (CDA’B’) bằng 90 độ.

HĐ9

Trả lời câu hỏi Hoạt động 9 trang 73 SGK Toán 12 Cánh diều

Cho hai mặt phẳng \(\left( {{P_1}} \right)\) và \(\left( {{P_2}} \right)\). Gọi \(\overrightarrow {{n_1}}  = \left( {{A_1};{B_1};{C_1}} \right),\overrightarrow {{n_2}}  = \left( {{A_2};{B_2};{C_2}} \right)\) lần lượt là hai vectơ pháp tuyến của \(\left( {{P_1}} \right)\), \(\left( {{P_2}} \right)\); \({\Delta _1},{\Delta _2}\) lần lượt là giá của hai vectơ \(\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} \) (Hình 33). So sánh:

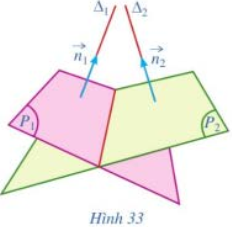
a) \(\cos \left( {\left( {{P_1}} \right),\left( {{P_2}} \right)} \right)\) và \(\cos \left( {{\Delta _1},{\Delta _2}} \right)\);

b) \(\cos \left( {{\Delta _1},{\Delta _2}} \right)\) và \(\left| {\cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)} \right|\).

Phương pháp giải:

Sử dụng kiến thức vectơ pháp tuyến của mặt phẳng để chứng minh: Nếu vectơ \(\overrightarrow n \) khác \(\overrightarrow 0 \) và có giá vuông góc với mặt phẳng (P) thì \(\overrightarrow n \) được gọi là vectơ pháp tuyến của mặt phẳng (P).

Sử dụng kiến thức về vectơ chỉ phương của đường thẳng để chứng minh: Cho đường thẳng \(\Delta \) và vectơ \(\overrightarrow u \) khác \(\overrightarrow 0 \). Vectơ \(\overrightarrow u \) được gọi là vectơ chỉ phương của đường thẳng \(\Delta \) nếu giá của \(\overrightarrow u \) song song hoặc trùng với \(\Delta \).

Lời giải chi tiết:

a) Vì \({\Delta _1} \bot \left( {{P_1}} \right)\) nên đường thẳng \({\Delta _1}\) nhận một vectơ pháp tuyến \(\overrightarrow {{n_1}} \) của mặt phẳng \(\left( {{P_1}} \right)\) làm một vectơ chỉ phương.

Vì \({\Delta _2} \bot \left( {{P_2}} \right)\) nên đường thẳng \({\Delta _2}\) nhận một vectơ pháp tuyến \(\overrightarrow {{n_2}} \) của mặt phẳng \(\left( {{P_2}} \right)\) làm một vectơ chỉ phương.

Do đó, góc giữa hai đường thẳng \({\Delta _1},{\Delta _2}\) là góc giữa hai vectơ pháp tuyến \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \).

Vậy \(\cos \left( {\left( {{P_1}} \right),\left( {{P_2}} \right)} \right) = \cos \left( {{\Delta _1},{\Delta _2}} \right)\).

b) Ta có:\(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \cos \left( {\left( {{P_1}} \right),\left( {{P_2}} \right)} \right) = \left| {\cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)} \right|\).

LT9

Trả lời câu hỏi Luyện tập 9 trang 73 SGK Toán 12 Cánh diều

Cho mặt phẳng (P) có vectơ pháp tuyến \(\overrightarrow n  = \left( {A;B;C} \right)\). Tính côsin của góc giữa mặt phẳng (P) và các mặt phẳng tọa độ.

Phương pháp giải:

Sử dụng kiến thức về côsin góc giữa hai mặt phẳng để tính: Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng \(\left( {{P_1}} \right)\), \(\left( {{P_2}} \right)\) có vectơ pháp tuyến lần lượt là \(\overrightarrow {{n_1}}  = \left( {{A_1};{B_1};{C_1}} \right)\), \(\overrightarrow {{n_2}}  = \left( {{A_2};{B_2};{C_2}} \right)\). Khi đó, ta có: \(\cos \left( {\left( {{P_1}} \right),\left( {{P_2}} \right)} \right) = \frac{{\left| {{A_1}{A_2} + {B_1}{B_2} + {C_1}{C_2}} \right|}}{{\sqrt {A_1^2 + B_1^2 + C_1^2} .\sqrt {A_2^2 + B_2^2 + C_2^2} }}\).

Lời giải chi tiết:

Mặt phẳng (Oxy) có một vectơ pháp tuyến là \(\overrightarrow k  = \left( {0;0;1} \right)\); mặt phẳng (Oxz) có một vectơ pháp tuyến là \(\overrightarrow j  = \left( {0;1;0} \right)\); mặt phẳng (Oyz) có một vectơ pháp tuyến là \(\overrightarrow i  = \left( {1;0;0} \right)\)

Do đó, \(\cos \left( {\left( {Oxy} \right),\left( P \right)} \right) = \frac{{\left| {0.A + 0.B + 1.C} \right|}}{{\sqrt {{0^2} + {0^2} + {1^2}} \sqrt {{A^2} + {B^2} + {C^2}} }} = \frac{{\left| C \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\);

\(\cos \left( {\left( {Oxz} \right),\left( P \right)} \right) = \frac{{\left| {0.A + 1.B + 0.C} \right|}}{{\sqrt {{0^2} + {1^2} + {0^2}} \sqrt {{A^2} + {B^2} + {C^2}} }} = \frac{{\left| B \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\);

\(\cos \left( {\left( {Oyz} \right),\left( P \right)} \right) = \frac{{\left| {1.A + 0.B + 0.C} \right|}}{{\sqrt {{1^2} + {0^2} + {0^2}} \sqrt {{A^2} + {B^2} + {C^2}} }} = \frac{{\left| A \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\).