 Toán 9 chân trời sáng tạo | Giải toán lớp 9 chân trời sáng tạo
Toán 9 chân trời sáng tạo | Giải toán lớp 9 chân trời sáng tạo
 Bài 1. Đường tròn - Toán 9 Chân trời sáng tạo
Bài 1. Đường tròn - Toán 9 Chân trời sáng tạo
Giải mục 2 trang 76, 77 SGK Toán 9 tập 1 - Chân trời sáng tạo
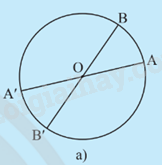
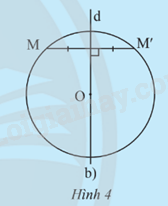
a) Cho đường tròn (O;R). i) Lấy điểm A nằm trên đường tròn. Vẽ đường thẳng AO cắt đường tròn tại điểm A’ khác A. Giải thích tại sao O là trung điểm của đoạn thẳng AA’. ii) Lấy điểm B khác A thuộc đường tròn (O;R). Tìm điểm B’ sao cho O trung điểm của đoạn thẳng BB’. Điểm B’ có thuộc đường tròn (O;R) không? Giải thích. b) Cho đường tròn (O;R), d là đường thẳng đi qua tâm O. Lấy điểm M nằm trên đường tròn. Vẽ điểm M’ sao cho d là đường trung trực của đoạn thẳng MM’ (khi M thuộc d thì lấy M’
HĐ2
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 76 SGK Toán 9 Chân trời sáng tạo
a) Cho đường tròn (O;R).
i) Lấy điểm A nằm trên đường tròn. Vẽ đường thẳng AO cắt đường tròn tại điểm A’ khác A. Giải thích tại sao O là trung điểm của đoạn thẳng AA’.
ii) Lấy điểm B khác A thuộc đường tròn (O;R). Tìm điểm B’ sao cho O trung điểm của đoạn thẳng BB’. Điểm B’ có thuộc đường tròn (O;R) không? Giải thích.
b) Cho đường tròn (O;R), d là đường thẳng đi qua tâm O. Lấy điểm M nằm trên đường tròn. Vẽ điểm M’ sao cho d là đường trung trực của đoạn thẳng MM’ (khi M thuộc d thì lấy M’ trùng với M). Điểm M’ có thuộc đường tròn (O;R) không? Giải thích.
Phương pháp giải:
Dựa vào khái niệm đường tròn để giải thích: Đường tròn tâm O bán kính R (R > 0) là hình gồm tất cả các điểm cách điểm O một khoảng bằng R.
Lời giải chi tiết:
a)
i) O là trung điểm của đoạn thẳng AA’ vì trong đường tròn (O;R): Hai điểm A và A’ đều cách điểm O một khoảng bằng R.
ii) Điểm B’ nằm đối xứng với B qua điểm O.
Điểm B’ cũng thuộc đường tròn (O;R) vì B nằm cách O một khoảng R nên B’ nằm cách O một khoảng R suy ra OB = OB’.
b) Điểm M’ cũng thuộc đường tròn (O;R) vì M’ là điểm đối xứng với M qua trung trực d.
TH1
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 1 trang 77 SGK Toán 9 Chân trời sáng tạo
Xác định tâm đối xứng và trục đối xứng của bánh xe trong Hình 7. Giải thích cách làm.

Phương pháp giải:
Dựa vào tính đối xứng của đường tròn:
+ Tâm đối xứng là tâm của đường tròn
+ Mọi đường thẳng đi qua tâm của đường tròn đều là trục đối xứng của nó.
Lời giải chi tiết:
Tâm đối xứng của bánh xe là trục ở giữa. (Đường tròn có 1 tâm đối xứng)
Trục đối xứng của bánh xe là đường thẳng đi qua trục ở giữa (Đường tròn có vô số tâm đối xứng).
VD1
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 1 trang 77 SGK Toán 9 Chân trời sáng tạo
Nêu cách chia một cái bánh có dạng hình tròn tâm O (Hình 8) thành hai phần bằng nhau.

Phương pháp giải:
Xác định một trục đối xứng của bánh.
Lời giải chi tiết:
Vẽ một trục đối xứng đi qua tâm O để chia bánh thành 2 phần bằng nhau.
- Giải mục 3 trang 77, 78 SGK Toán 9 tập 1 - Chân trời sáng tạo
- Giải mục 4 trang 78, 79, 80 SGK Toán 9 tập 1 - Chân trời sáng tạo
- Giải bài tập 1 trang 82 SGK Toán 9 tập 1 - Chân trời sáng tạo
- Giải bài tập 2 trang 82 SGK Toán 9 tập 1 - Chân trời sáng tạo
- Giải bài tập 3 trang 82 SGK Toán 9 tập 1 - Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Chân trời sáng tạo - Xem ngay












Danh sách bình luận